Come Si Trova Il Perimetro Di Un Triangolo Rettangolo

Vi siete mai chiesti come calcolare la distanza totale attorno a un oggetto? Questo concetto, chiamato perimetro, è fondamentale in molti aspetti della nostra vita, dall'incorniciare un quadro al progettare un giardino. In questo articolo, ci concentreremo su un tipo specifico di forma: il triangolo rettangolo. Impareremo insieme come trovarne il perimetro in modo semplice e chiaro. Questo articolo è pensato per studenti di scuola media e superiore, appassionati di geometria e chiunque voglia rinfrescare le proprie conoscenze matematiche.

Cos'è un Triangolo Rettangolo?

Prima di immergerci nel calcolo del perimetro, ripassiamo brevemente cosa rende un triangolo... un triangolo rettangolo!

• Un triangolo è una figura geometrica con tre lati e tre angoli.
• Un triangolo rettangolo è un triangolo che ha un angolo retto, ovvero un angolo di 90 gradi. Questo angolo è spesso indicato con un piccolo quadrato nell'angolo.
• I due lati che formano l'angolo retto sono chiamati cateti. Uno è l'altezza e l'altro la base.
• Il lato opposto all'angolo retto è chiamato ipotenusa, ed è il lato più lungo del triangolo rettangolo.

Immaginate una fetta di pizza perfettamente tagliata a partire dal centro: quella è una rappresentazione perfetta di un triangolo rettangolo! L'angolo formato dal taglio è di 90 gradi.

Definizione di Perimetro

Il perimetro di qualsiasi figura geometrica bidimensionale è la lunghezza totale del suo contorno. In altre parole, è la distanza che percorrereste se camminaste lungo tutti i lati della figura, partendo da un punto e tornando allo stesso punto. Pensate a recintare un giardino: la lunghezza totale della recinzione necessaria è il perimetro del giardino!

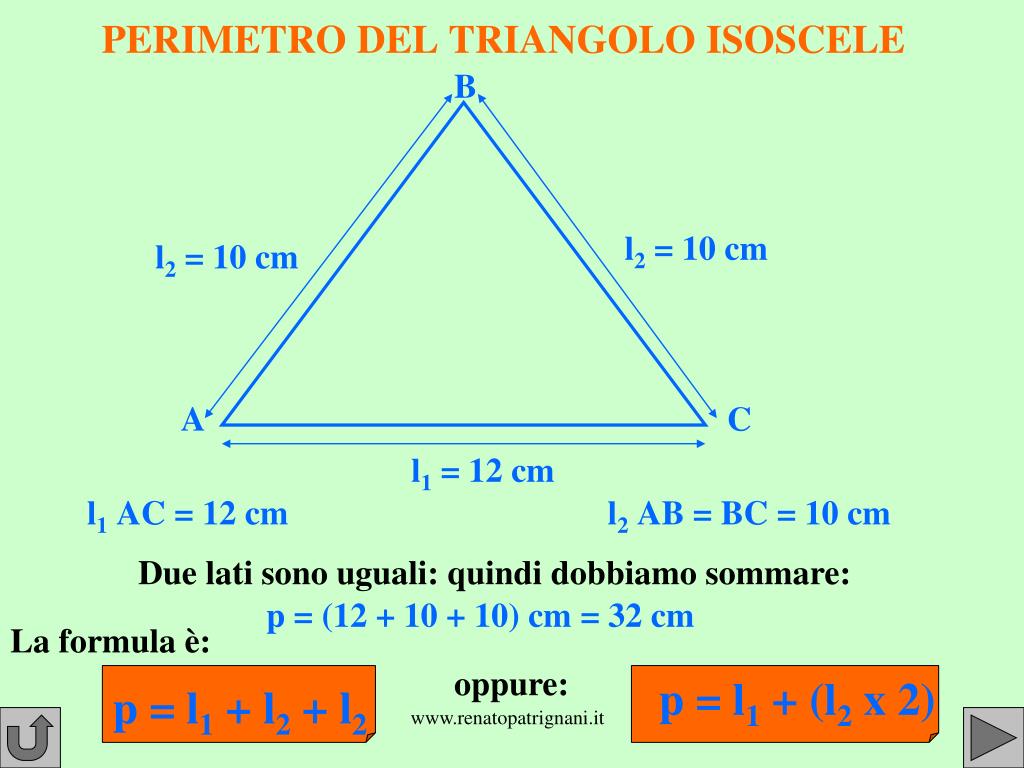
Quindi, per un triangolo rettangolo, il perimetro è semplicemente la somma delle lunghezze dei suoi tre lati: i due cateti e l'ipotenusa.

Come Calcolare il Perimetro di un Triangolo Rettangolo

Ora veniamo al dunque: come calcoliamo il perimetro di un triangolo rettangolo? Ci sono due scenari principali:

Scenario 1: Conosciamo le Lunghezze di Tutti e Tre i Lati

Questo è lo scenario più semplice. Se conosciamo le lunghezze dei due cateti (a e b) e dell'ipotenusa (c), allora il perimetro (P) si calcola con la seguente formula:

P = a + b + c

Esempio: Supponiamo di avere un triangolo rettangolo con un cateto di 3 cm, un altro cateto di 4 cm e un'ipotenusa di 5 cm. Il perimetro sarebbe:

P = 3 cm + 4 cm + 5 cm = 12 cm

Quindi, il perimetro di questo triangolo rettangolo è di 12 cm.

Scenario 2: Conosciamo le Lunghezze dei Due Cateti, ma non dell'Ipotenusa

Questo è un po' più impegnativo, ma non preoccupatevi, abbiamo lo strumento giusto: il Teorema di Pitagora!

Il Teorema di Pitagora

Il Teorema di Pitagora è un principio fondamentale della geometria che mette in relazione le lunghezze dei lati di un triangolo rettangolo. Afferma che:

a² + b² = c²

Dove:

• a e b sono le lunghezze dei due cateti.
• c è la lunghezza dell'ipotenusa.

In parole semplici, il quadrato dell'ipotenusa è uguale alla somma dei quadrati dei due cateti. Questo teorema è essenziale per risolvere molti problemi di geometria, non solo per i triangoli rettangoli!

Come Usare il Teorema di Pitagora per Trovare l'Ipotenusa

Se conosciamo le lunghezze dei due cateti (a e b), possiamo usare il Teorema di Pitagora per trovare la lunghezza dell'ipotenusa (c). Ecco i passaggi:

1. Calcola il quadrato di a (a²).
2. Calcola il quadrato di b (b²).
3. Somma a² e b².
4. Trova la radice quadrata della somma ottenuta. Questa radice quadrata è la lunghezza dell'ipotenusa (c).

Matematicamente:

c = √ (a² + b²)

Esempio: Supponiamo di avere un triangolo rettangolo con un cateto di 6 cm e un altro cateto di 8 cm. Vogliamo trovare la lunghezza dell'ipotenusa.

1. a² = 6² = 36
2. b² = 8² = 64
3. a² + b² = 36 + 64 = 100
4. c = √100 = 10 cm

Quindi, l'ipotenusa di questo triangolo rettangolo è di 10 cm.

Calcolo del Perimetro

Ora che abbiamo trovato la lunghezza dell'ipotenusa, possiamo calcolare il perimetro usando la formula:

P = a + b + c

Nel nostro esempio:

P = 6 cm + 8 cm + 10 cm = 24 cm

Quindi, il perimetro di questo triangolo rettangolo è di 24 cm.

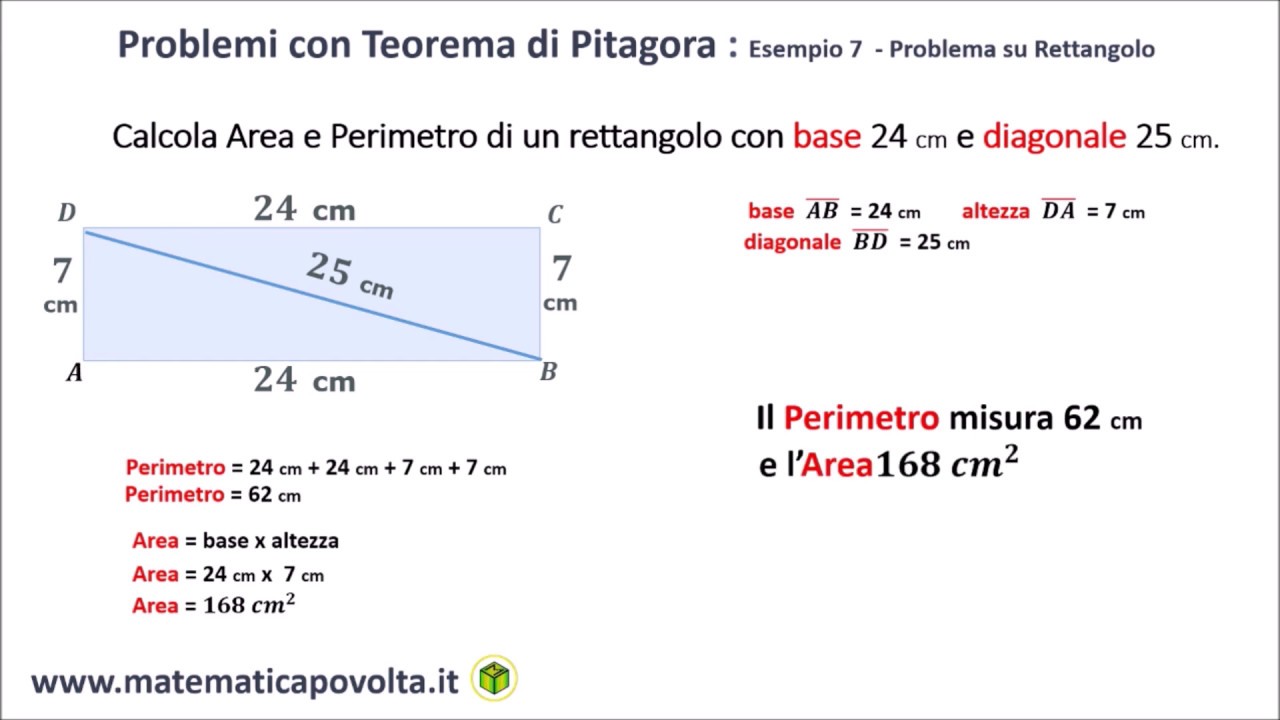
Scenario 3: Conosciamo l'Ipotenusa e un Cateto

In questo scenario, possiamo ancora usare il Teorema di Pitagora per trovare il cateto mancante. Supponiamo di conoscere l'ipotenusa (c) e un cateto (a). Dobbiamo trovare l'altro cateto (b).

Dal Teorema di Pitagora: a² + b² = c², possiamo ricavare b²:

b² = c² - a²

E quindi:

b = √(c² - a²)

Esempio: Immaginiamo un triangolo rettangolo con ipotenusa di 13 cm e un cateto di 5 cm. Calcoliamo l'altro cateto:

b = √(13² - 5²) = √(169 - 25) = √144 = 12 cm

Ora che abbiamo entrambi i cateti e l'ipotenusa, possiamo calcolare il perimetro:

P = 5 cm + 12 cm + 13 cm = 30 cm

Esercizi Pratici

Per consolidare la vostra comprensione, provate a risolvere questi esercizi:

1. Un triangolo rettangolo ha cateti di lunghezza 5 cm e 12 cm. Trova il suo perimetro.
2. Un triangolo rettangolo ha un cateto di lunghezza 8 cm e un'ipotenusa di 17 cm. Trova il suo perimetro.
3. Un triangolo rettangolo ha un'area di 30 cm² e un cateto di 5 cm. Trova il suo perimetro. (Suggerimento: ricorda che l'area di un triangolo è (base * altezza) / 2)

Applicazioni Pratiche

Il calcolo del perimetro di un triangolo rettangolo non è solo un esercizio teorico. Ha molte applicazioni pratiche in diversi campi, tra cui:

• Architettura e Ingegneria: Calcolare le lunghezze dei lati di un tetto, di una rampa o di altre strutture triangolari.
• Falegnameria: Determinare la quantità di materiale necessaria per costruire una cornice triangolare o un altro oggetto.
• Geodesia e Cartografia: Misurare distanze e aree in terreni irregolari.
• Navigazione: Calcolare la distanza tra due punti usando la trigonometria.
• Videogiochi: Determinare le collisioni tra oggetti e calcolare le traiettorie.

Quindi, la prossima volta che vedete un triangolo rettangolo, ricordatevi che siete in grado di calcolarne il perimetro! La matematica è ovunque, e saperla usare ci rende più consapevoli e capaci di comprendere il mondo che ci circonda.

Conclusione

Abbiamo esplorato insieme come trovare il perimetro di un triangolo rettangolo, passando dalla definizione di triangolo rettangolo al fondamentale Teorema di Pitagora. Abbiamo visto come applicare questi concetti in diverse situazioni, sia teoriche che pratiche. Spero che questo articolo vi abbia fornito gli strumenti e la fiducia necessari per affrontare qualsiasi problema relativo al perimetro di un triangolo rettangolo. Ricordate, la pratica rende perfetti! Continuate a esercitarvi e non abbiate paura di esplorare nuove sfide matematiche.