Come Si Trova Il Perimetro Di Un Triangolo Isoscele

Ti sei mai trovato di fronte a un problema di geometria che ti sembrava insormontabile? Magari un compito a casa con un triangolo isoscele che ti fissava dallo schermo, chiedendoti di calcolarne il perimetro? Niente panico! La geometria, a volte, può sembrare un labirinto di formule, ma con la giusta guida e un po' di pazienza, ogni problema può essere risolto. Questo articolo è qui per aiutarti a navigare nel mondo dei triangoli isosceli e a calcolare il loro perimetro con facilità. Non importa se sei uno studente alle prime armi o se hai solo bisogno di rinfrescare le tue conoscenze, troverai qui tutto quello che ti serve.

Cos'è un Triangolo Isoscele?

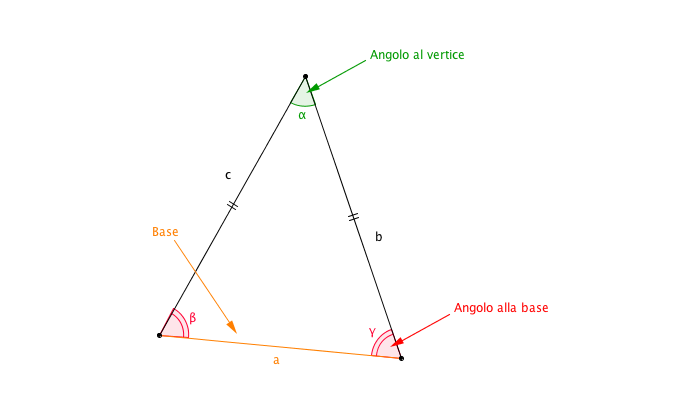
Prima di addentrarci nel calcolo del perimetro, è fondamentale capire cosa rende un triangolo isoscele speciale. Un triangolo isoscele è un triangolo che ha due lati di uguale lunghezza. Questi due lati uguali sono chiamati lati obliqui, mentre il terzo lato è chiamato base. Un'altra caratteristica importante è che gli angoli alla base, ovvero gli angoli opposti ai lati obliqui, sono anch'essi uguali. Questa proprietà sarà utile per risolvere alcuni problemi più complessi.

Pensa ad esempio alla forma di un tetto a due falde. Molto spesso, il tetto visto frontalmente ha la forma di un triangolo isoscele. Questo rende più facile visualizzare le proprietà di questo tipo di triangolo nella vita di tutti i giorni.

Perimetro di un Triangolo Isoscele: La Formula Fondamentale

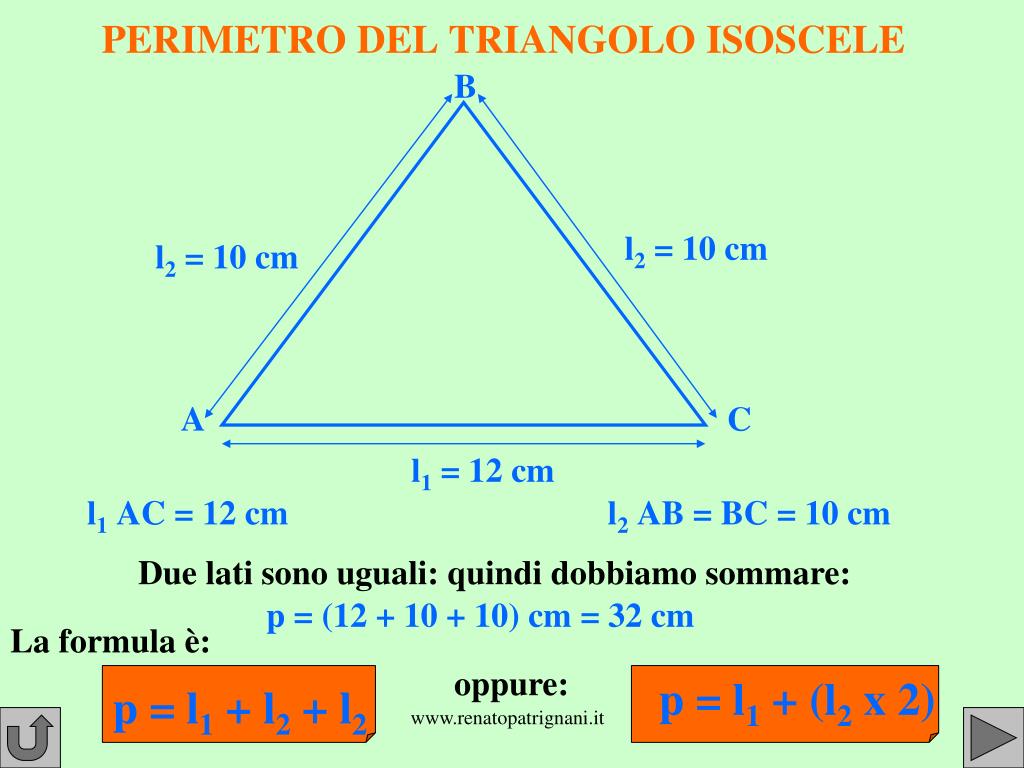
Il perimetro di qualsiasi figura geometrica è la somma della lunghezza di tutti i suoi lati. Quindi, per un triangolo isoscele, il calcolo del perimetro è piuttosto semplice:

Perimetro = Lato Obliquo + Lato Obliquo + Base

Possiamo anche scrivere la formula in modo più compatto:

Perimetro = 2 * Lato Obliquo + Base

Questa formula è la chiave per risolvere la maggior parte dei problemi relativi al perimetro di un triangolo isoscele. Vediamo come applicarla in pratica.

Esempio Pratico 1: Conosciamo Lato Obliquo e Base

Supponiamo di avere un triangolo isoscele con un lato obliquo di 8 cm e una base di 5 cm. Qual è il suo perimetro?

Applichiamo la formula:

Perimetro = 2 * 8 cm + 5 cm = 16 cm + 5 cm = 21 cm

Quindi, il perimetro del triangolo è di 21 cm.

Esempio Pratico 2: Conosciamo il Perimetro e il Lato Obliquo

Questa volta, immaginiamo di conoscere il perimetro di un triangolo isoscele, che è di 30 cm, e la lunghezza di un lato obliquo, che è di 10 cm. Vogliamo trovare la lunghezza della base.

Usiamo la formula del perimetro e la riarrangiamo per trovare la base:

Perimetro = 2 * Lato Obliquo + Base

30 cm = 2 * 10 cm + Base

30 cm = 20 cm + Base

Base = 30 cm - 20 cm = 10 cm

In questo caso, la base del triangolo è lunga 10 cm. Questo significa che il triangolo è in realtà un triangolo equilatero, poiché tutti e tre i lati sono uguali! Un triangolo equilatero è un caso speciale di triangolo isoscele.

Cosa Fare Quando Conosciamo Solo l'Altezza e la Base?

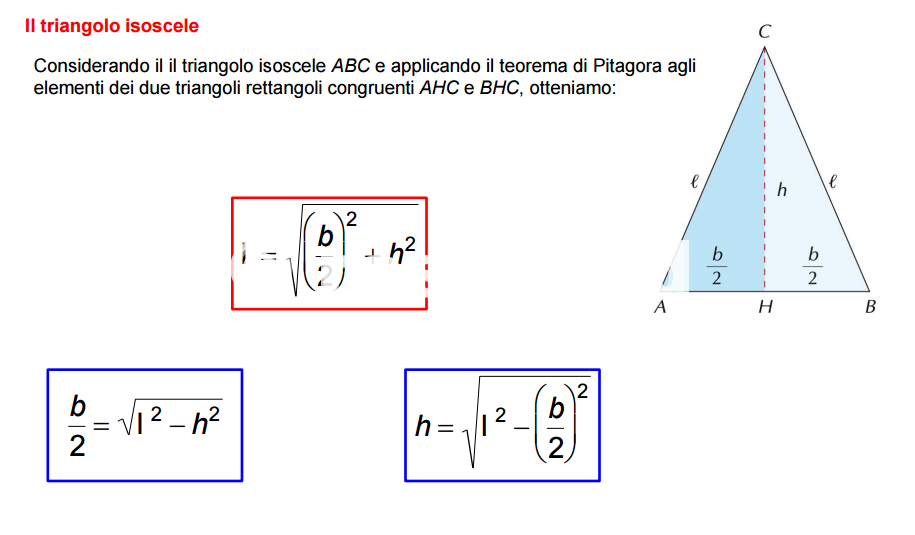
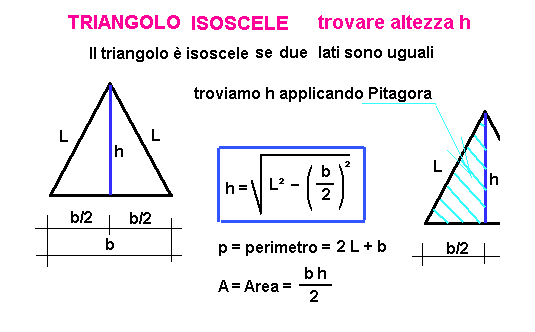
A volte, il problema non ci fornisce direttamente la lunghezza del lato obliquo. Invece, potremmo conoscere l'altezza del triangolo (la distanza perpendicolare dalla base al vertice opposto) e la lunghezza della base. In questo caso, dobbiamo usare il Teorema di Pitagora per trovare la lunghezza del lato obliquo.

Ricorda che l'altezza di un triangolo isoscele divide la base in due parti uguali. Questo significa che possiamo considerare un triangolo rettangolo formato dall'altezza, metà della base e il lato obliquo come ipotenusa.

Il Teorema di Pitagora afferma che in un triangolo rettangolo:

a² + b² = c²

Dove 'a' e 'b' sono i cateti (i lati che formano l'angolo retto) e 'c' è l'ipotenusa (il lato opposto all'angolo retto).

Nel nostro caso:

a = Altezza
b = Base / 2
c = Lato Obliquo

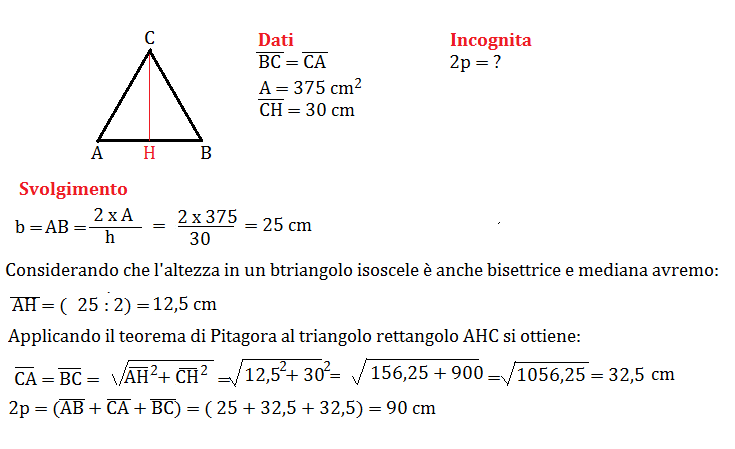
Esempio Pratico 3: Altezza e Base Conosciute

Supponiamo di avere un triangolo isoscele con un'altezza di 6 cm e una base di 8 cm. Vogliamo calcolare il perimetro.

Calcoliamo metà della base: Base / 2 = 8 cm / 2 = 4 cm
Applichiamo il Teorema di Pitagora: 6² + 4² = Lato Obliquo² => 36 + 16 = Lato Obliquo² => 52 = Lato Obliquo²
Calcoliamo la radice quadrata per trovare il lato obliquo: Lato Obliquo = √52 ≈ 7.21 cm
Calcoliamo il perimetro: Perimetro = 2 * 7.21 cm + 8 cm = 14.42 cm + 8 cm = 22.42 cm

Quindi, il perimetro del triangolo è di circa 22.42 cm.

Consigli Utili per Risolvere i Problemi

Disegna sempre un diagramma: Un disegno ti aiuterà a visualizzare il problema e a identificare le informazioni che hai e quelle che devi trovare.
Scrivi le formule: Avere le formule a portata di mano ti eviterà errori e ti aiuterà a capire meglio la relazione tra le diverse grandezze.
Controlla le unità di misura: Assicurati che tutte le misure siano espresse nella stessa unità (ad esempio, tutti in cm o tutti in metri) prima di effettuare i calcoli.
Sii paziente: La geometria richiede pratica e pazienza. Non scoraggiarti se all'inizio incontri difficoltà. Rileggi attentamente il problema e prova diverse strategie.
Usa una calcolatrice: Per calcoli più complessi, soprattutto quando si usa il Teorema di Pitagora e si devono calcolare radici quadrate, una calcolatrice scientifica può essere molto utile.

Applicazioni Pratiche del Perimetro di un Triangolo Isoscele

La conoscenza del perimetro di un triangolo isoscele non è solo un esercizio di geometria teorica. Trova applicazione in diversi campi, come:

Architettura: Per calcolare la quantità di materiale necessario per costruire tetti, facciate o altre strutture a forma di triangolo isoscele.
Ingegneria: Per progettare ponti, travi e altre strutture che utilizzano triangoli isosceli per la loro stabilità.
Design: Per creare oggetti decorativi, mobili o altri prodotti con forme triangolari.
Artigianato: Per realizzare patchwork, quilting o altre creazioni artistiche che utilizzano triangoli isosceli.

Ad esempio, immagina di voler costruire una recinzione per un'aiuola a forma di triangolo isoscele. Calcolare il perimetro ti permetterà di sapere quanta recinzione devi acquistare.

Conclusione

Speriamo che questa guida ti abbia chiarito come trovare il perimetro di un triangolo isoscele. Ricorda, la chiave è capire le proprietà del triangolo, conoscere la formula fondamentale e, se necessario, saper applicare il Teorema di Pitagora. Con un po' di pratica, sarai in grado di risolvere qualsiasi problema di perimetro di un triangolo isoscele con facilità. Non aver paura di affrontare le sfide geometriche: ogni problema risolto è un passo avanti nella tua comprensione del mondo che ti circonda!