Come Si Trova Il Lato Obliquo Del Trapezio Rettangolo

Ti sei mai trovato di fronte a un problema di geometria che sembrava insormontabile? Magari un esercizio sul trapezio rettangolo, dove ti veniva chiesto di calcolare il lato obliquo, e ti sentivi completamente bloccato? Non preoccuparti, capita a tutti! La geometria può sembrare ostica a volte, ma con gli strumenti giusti e una spiegazione chiara, anche il problema più complesso può essere risolto.

In questo articolo, ti guiderò passo dopo passo alla scoperta di come trovare il lato obliquo di un trapezio rettangolo. Non useremo termini difficili o formule incomprensibili. L'obiettivo è rendere il processo il più semplice e intuitivo possibile, in modo che tu possa affrontare qualsiasi problema di geometria con sicurezza e tranquillità.

Che tu sia uno studente alle prese con i compiti, un appassionato di matematica desideroso di approfondire le tue conoscenze, o semplicemente qualcuno che ha bisogno di rinfrescare le proprie nozioni di geometria, questo articolo è pensato per te.

Comprendere il Trapezio Rettangolo: Le Basi

Prima di immergerci nel calcolo del lato obliquo, è fondamentale capire bene cos'è un trapezio rettangolo e quali sono le sue caratteristiche principali.

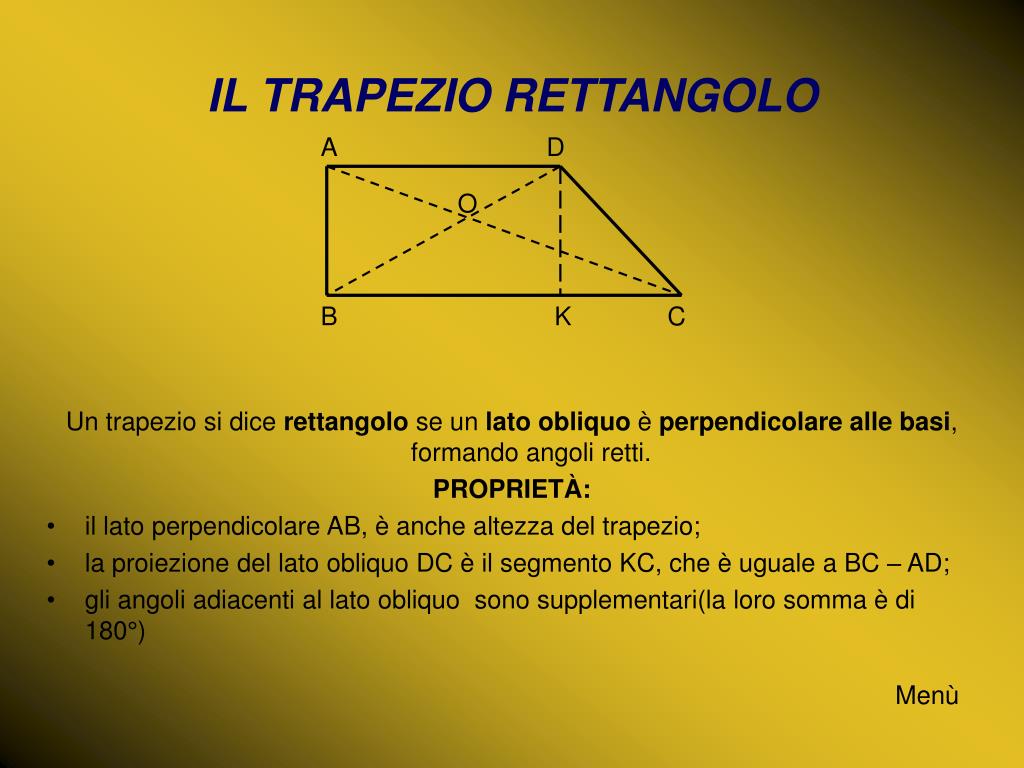
Un trapezio rettangolo è un quadrilatero con due lati paralleli (le basi) e due angoli retti. Questo significa che uno dei lati non paralleli è perpendicolare alle basi, formando appunto gli angoli di 90 gradi. Immagina una forma simile a un quadrato o rettangolo con un lato leggermente inclinato: ecco, quello è un trapezio rettangolo!

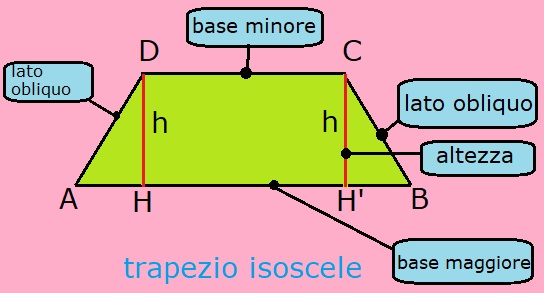
Elementi chiave di un trapezio rettangolo:

Base Maggiore (B): Il lato parallelo più lungo.
Base Minore (b): Il lato parallelo più corto.
Altezza (h): Il lato perpendicolare alle basi (e quindi, uno dei lati non paralleli).
Lato Obliquo (l): L'altro lato non parallelo, quello inclinato, che è proprio quello che vogliamo calcolare!

Capire bene questi elementi è cruciale. Pensa al trapezio rettangolo come a un insieme di pezzi, dove ogni pezzo ha un ruolo specifico. Conoscere questi ruoli ti permetterà di applicare le formule corrette e risolvere il problema.

Il Teorema di Pitagora: Il Nostro Alleato

Il Teorema di Pitagora è uno strumento potentissimo in geometria, e ci sarà di grande aiuto per trovare il lato obliquo del trapezio rettangolo. Ricorda, il teorema di Pitagora si applica solo ai triangoli rettangoli.

Cosa dice il teorema di Pitagora? In un triangolo rettangolo, il quadrato dell'ipotenusa (il lato opposto all'angolo retto) è uguale alla somma dei quadrati dei cateti (i due lati che formano l'angolo retto).

In formula: a² + b² = c²

Dove:

a e b sono i cateti
c è l'ipotenusa

Come applichiamo il teorema di Pitagora al trapezio rettangolo?

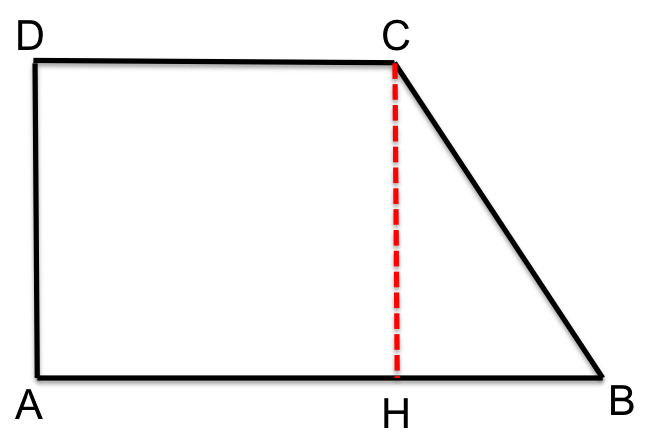
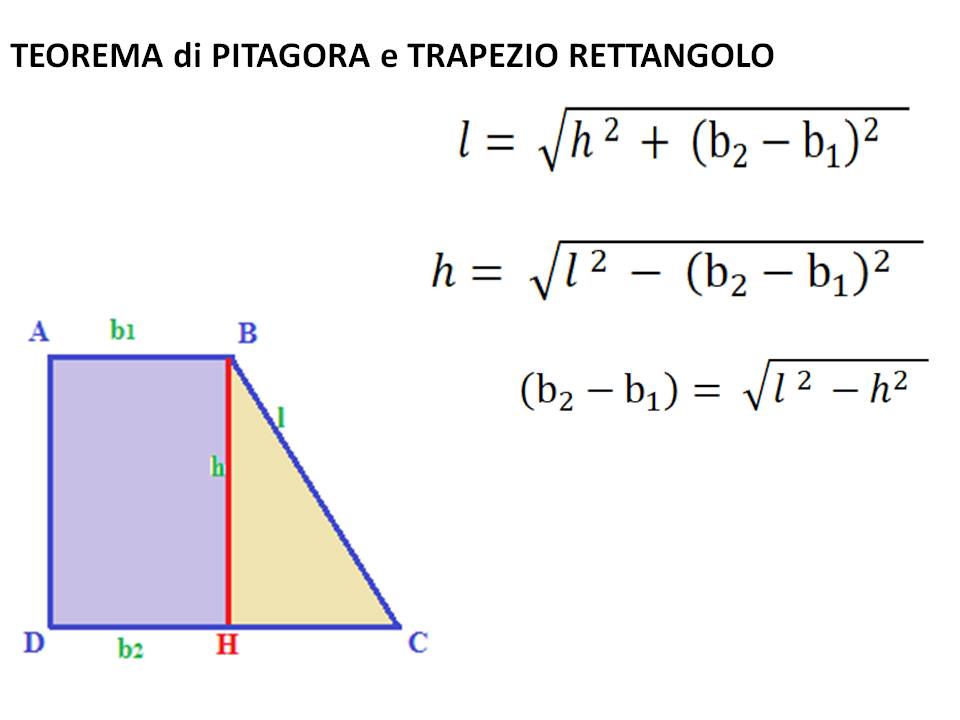
L'idea è di "trasformare" il nostro trapezio rettangolo in un triangolo rettangolo. Immagina di tracciare una linea perpendicolare dalla base minore alla base maggiore. Questa linea è parallela all'altezza del trapezio e ha la stessa lunghezza. In questo modo, hai creato un rettangolo e, soprattutto, un triangolo rettangolo!

Nel triangolo rettangolo che abbiamo creato:

L'ipotenusa è il lato obliquo (l) del trapezio.
Un cateto è l'altezza (h) del trapezio.
L'altro cateto è la differenza tra la base maggiore (B) e la base minore (b), ovvero (B - b).

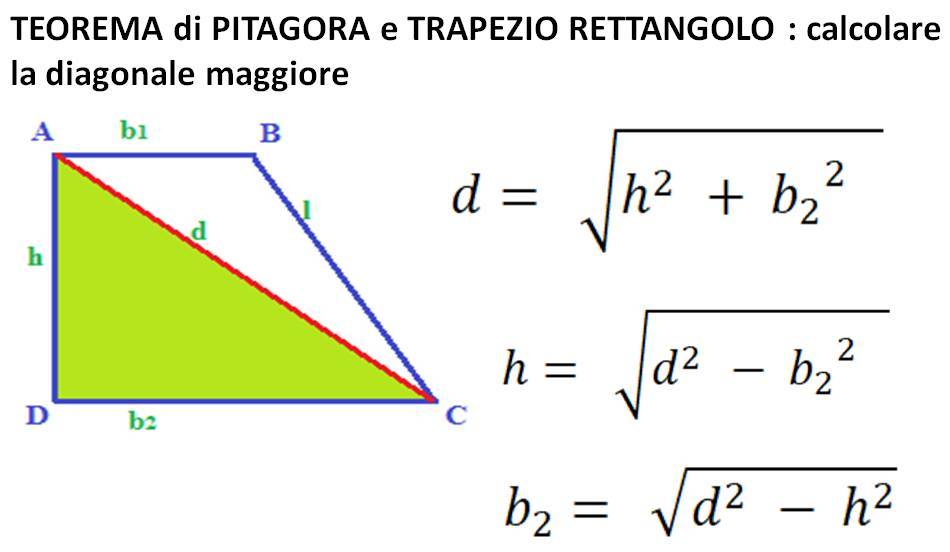
Ora possiamo applicare il teorema di Pitagora: (B - b)² + h² = l²

Calcolare il Lato Obliquo: La Formula e l'Esempio

Finalmente siamo pronti a calcolare il lato obliquo! Dalla formula del teorema di Pitagora, possiamo ricavare la formula per calcolare il lato obliquo:

l = √[(B - b)² + h²]

Questa formula ti permette di trovare il lato obliquo (l) conoscendo la base maggiore (B), la base minore (b) e l'altezza (h) del trapezio rettangolo.

Esempio pratico:

Supponiamo di avere un trapezio rettangolo con:

Base maggiore (B) = 10 cm
Base minore (b) = 6 cm
Altezza (h) = 3 cm

Applichiamo la formula:

l = √[(10 - 6)² + 3²]

l = √[4² + 9]

l = √[16 + 9]

l = √25

l = 5 cm

Quindi, il lato obliquo del trapezio rettangolo è di 5 cm.

Ricorda: È fondamentale prestare attenzione alle unità di misura. Assicurati che tutte le misure siano espresse nella stessa unità (es. tutti in centimetri, o tutti in metri) prima di applicare la formula.

Consigli e Trucchi Utili

Ecco alcuni consigli per rendere il calcolo del lato obliquo ancora più semplice:

Disegna sempre la figura: Disegnare il trapezio rettangolo ti aiuta a visualizzare il problema e a identificare correttamente le basi, l'altezza e il lato obliquo.
Scrivi la formula: Prima di iniziare a calcolare, scrivi la formula del teorema di Pitagora e la formula derivata per il calcolo del lato obliquo. Questo ti aiuta a non commettere errori.
Controlla i calcoli: Ricontrolla sempre i calcoli per assicurarti di non aver fatto errori di distrazione.
Usa una calcolatrice: Se i numeri sono complessi, usa una calcolatrice per semplificare i calcoli.
Esercitati: Più ti eserciti, più diventerai bravo a risolvere problemi di geometria. Prova a risolvere diversi esercizi con diversi valori di base maggiore, base minore e altezza.
Scomponi il problema: Se il problema sembra troppo difficile, prova a scomporlo in passaggi più semplici. Identifica il triangolo rettangolo e applica il teorema di Pitagora passo dopo passo.

Non aver paura di chiedere aiuto! Se ti blocchi, chiedi aiuto al tuo insegnante, a un compagno di classe o a un tutor. Ci sono anche molte risorse online, come video tutorial e forum di matematica, che possono aiutarti a capire meglio il concetto.

Conclusioni

Calcolare il lato obliquo di un trapezio rettangolo può sembrare difficile all'inizio, ma con la giusta comprensione dei concetti di base e con l'aiuto del teorema di Pitagora, diventa un compito accessibile a tutti.

Ricorda i passaggi chiave: identificare gli elementi del trapezio rettangolo, creare un triangolo rettangolo, applicare il teorema di Pitagora e utilizzare la formula per calcolare il lato obliquo.

Spero che questo articolo ti sia stato utile. Ora hai gli strumenti necessari per affrontare qualsiasi problema di geometria che ti si presenti. Continua a esercitarti e non arrenderti di fronte alle difficoltà. La geometria è un mondo affascinante, e con un po' di impegno, puoi padroneggiarla!