Come Si Trova Area Del Rombo

Hai mai guardato un aquilone volare alto nel cielo, o ammirato le intricate decorazioni di un pavimento piastrellato? Molto probabilmente, hai incontrato un rombo. Ma sai come calcolarne l'area? Se la risposta è no, o se vuoi semplicemente rinfrescare le tue conoscenze, sei nel posto giusto! Questa guida completa ti accompagnerà passo dopo passo alla scoperta di tutti i segreti per calcolare l'area di un rombo, rendendo la geometria un gioco da ragazzi.

Cos'è un Rombo e Perché Calcolarne l'Area?

Prima di addentrarci nei calcoli, definiamo cos'è un rombo. Un rombo è un quadrilatero (una figura geometrica a quattro lati) con le seguenti caratteristiche:

• Tutti e quattro i lati sono congruenti (cioè, hanno la stessa lunghezza).
• Le diagonali si intersecano perpendicolarmente (formando angoli retti).
• Le diagonali si bisecano a vicenda (si dividono a metà nel punto di intersezione).

Ma perché è importante saper calcolare l'area di un rombo? Le applicazioni sono molteplici! Pensiamo ad esempio a:

• Architettura: Molte strutture architettoniche incorporano rombi nel loro design. Calcolare l'area permette di stimare la quantità di materiali necessari per la costruzione.
• Design: I rombi sono utilizzati in pavimentazioni, rivestimenti e decorazioni. Conoscere la loro area aiuta a pianificare la disposizione e a calcolare i costi.
• Ingegneria: Nella progettazione di ponti e strutture, i rombi possono essere utilizzati come elementi strutturali. Calcolare la loro area è fondamentale per garantire la stabilità e la resistenza.
• Matematica e Geometria: Lo studio del rombo e del calcolo della sua area rafforza le basi della geometria e del pensiero logico-deduttivo.

Quindi, imparare a calcolare l'area di un rombo non è solo un esercizio teorico, ma un'abilità pratica che può essere utile in diverse situazioni.

Metodo 1: Usando le Diagonali

Il metodo più comune e diretto per calcolare l'area di un rombo è utilizzare la lunghezza delle sue diagonali. Ricorda, le diagonali sono i segmenti che collegano due vertici opposti del rombo.

La formula è semplice:

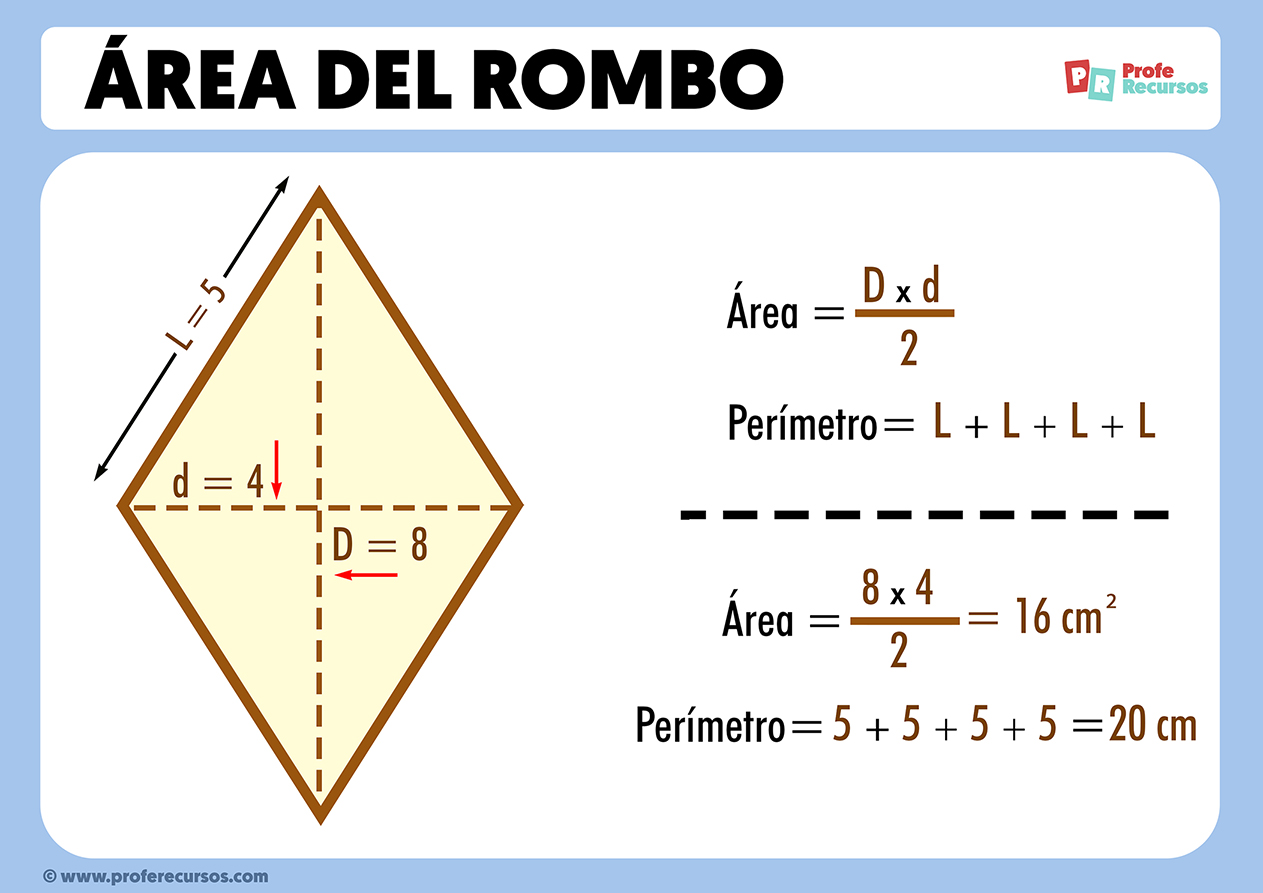
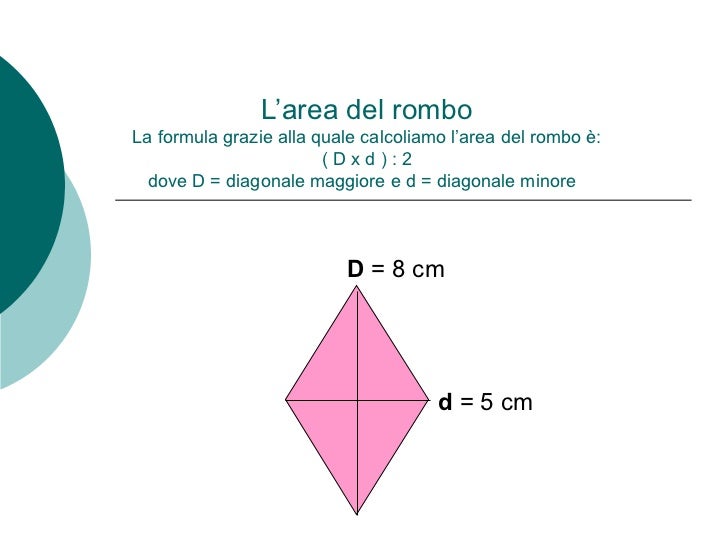
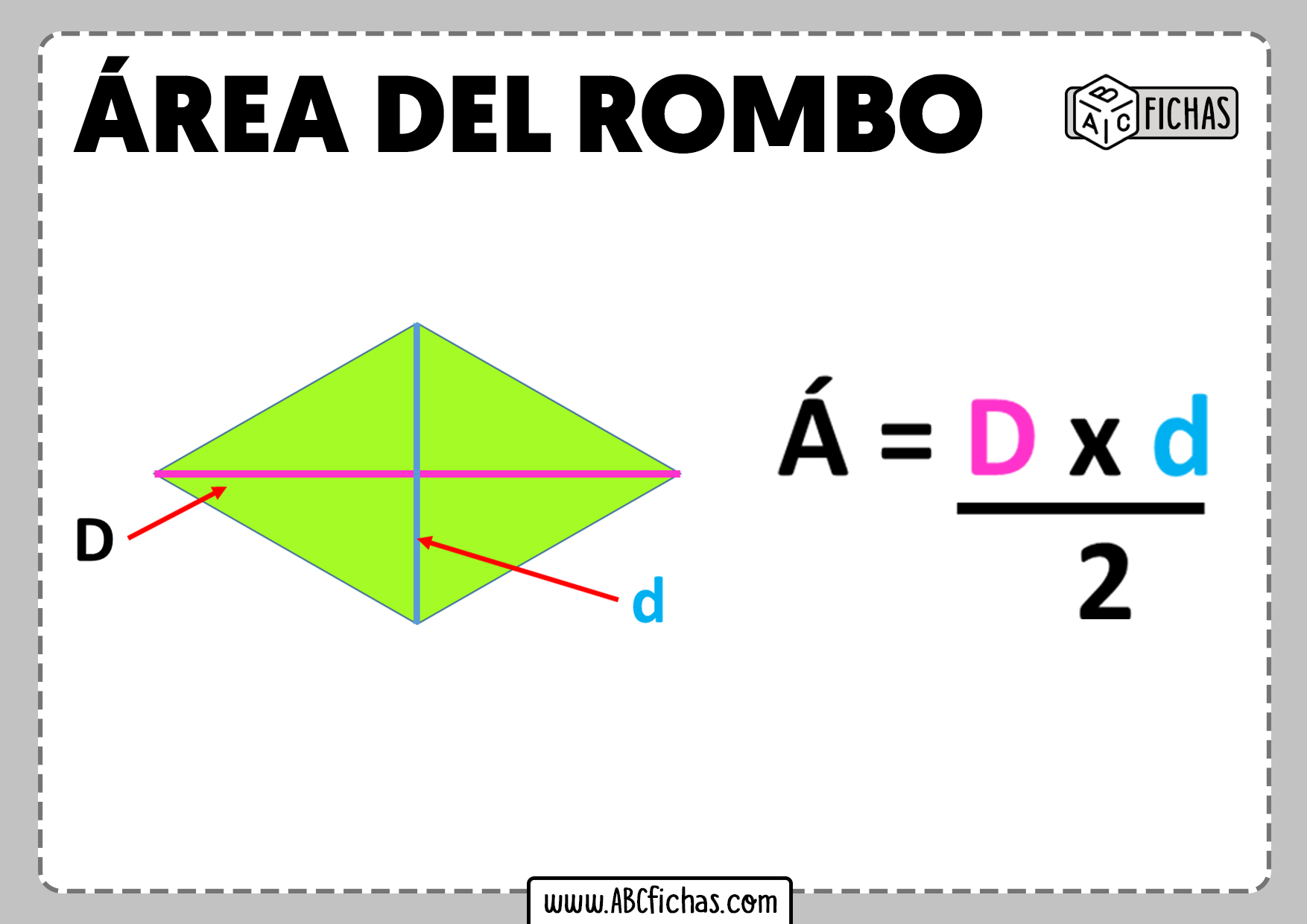
Area del Rombo = (Diagonale Maggiore × Diagonale Minore) / 2

Dove:

• Diagonale Maggiore è la lunghezza della diagonale più lunga.
• Diagonale Minore è la lunghezza della diagonale più corta.

Esempio Pratico:

Immagina di avere un rombo con una diagonale maggiore di 10 cm e una diagonale minore di 6 cm. Applichiamo la formula:

Area = (10 cm × 6 cm) / 2 = 60 cm² / 2 = 30 cm²

Quindi, l'area del rombo è di 30 cm².

Perché Funziona?

Puoi visualizzare il rombo come due triangoli congruenti uniti per la base. L'area di ogni triangolo è (base × altezza) / 2. La base del triangolo è una diagonale del rombo, e l'altezza è metà dell'altra diagonale. Sommando le aree dei due triangoli, si ottiene la formula per l'area del rombo.

Metodo 2: Usando il Lato e l'Altezza

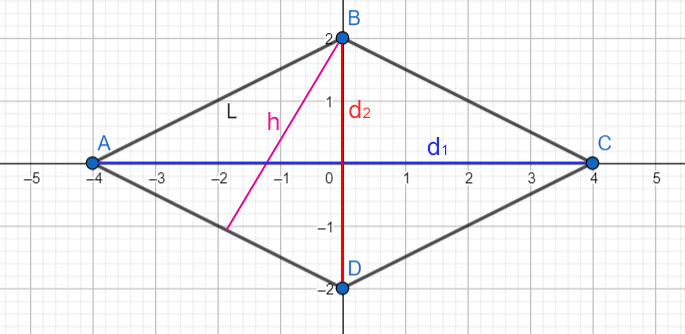
Un altro metodo per calcolare l'area di un rombo è utilizzare la lunghezza di un lato e l'altezza relativa a quel lato. Ricorda, l'altezza è la distanza perpendicolare tra un lato e il suo lato opposto.

La formula è analoga a quella per calcolare l'area di un parallelogramma:

Area del Rombo = Lato × Altezza

Dove:

• Lato è la lunghezza di uno qualsiasi dei lati del rombo (dato che sono tutti uguali).
• Altezza è la distanza perpendicolare tra quel lato e il suo lato opposto.

Esempio Pratico:

Supponiamo di avere un rombo con un lato di 8 cm e un'altezza di 5 cm. Applichiamo la formula:

Area = 8 cm × 5 cm = 40 cm²

Quindi, l'area del rombo è di 40 cm².

Quando Usare Questo Metodo?

Questo metodo è particolarmente utile quando conosciamo la lunghezza del lato e l'altezza, o quando possiamo facilmente misurarle. Ad esempio, se il rombo è disegnato su un piano cartesiano, possiamo calcolare facilmente la lunghezza del lato e l'altezza usando le coordinate dei vertici.

Metodo 3: Usando la Trigonometria

Se conosciamo la lunghezza di un lato e l'angolo tra due lati adiacenti, possiamo utilizzare la trigonometria per calcolare l'area del rombo. Sia l la lunghezza del lato e θ l'angolo tra due lati adiacenti.

La formula è:

Area del Rombo = l² × sin(θ)

Dove:

• l è la lunghezza del lato del rombo.
• θ è l'angolo tra due lati adiacenti (espresso in gradi o radianti).

Esempio Pratico:

Immaginiamo un rombo con un lato di 7 cm e un angolo di 60° tra due lati adiacenti. Applichiamo la formula:

Area = 7² cm² × sin(60°) = 49 cm² × √3/2 ≈ 42.44 cm²

Quindi, l'area del rombo è di circa 42.44 cm².

Perché Funziona?

Questo metodo si basa sulla scomposizione del rombo in due triangoli congruenti. L'area di ogni triangolo può essere calcolata usando la formula (1/2) * a * b * sin(C), dove a e b sono le lunghezze di due lati e C è l'angolo tra di essi. In questo caso, a = b = l (il lato del rombo) e C = θ (l'angolo tra i lati). Moltiplicando per due l'area del triangolo, si ottiene l'area del rombo.

Scegliere il Metodo Giusto

Ora che conosciamo diversi metodi per calcolare l'area di un rombo, come scegliere quello più appropriato? La risposta dipende dalle informazioni a nostra disposizione:

• Se conosciamo le lunghezze delle diagonali: Utilizza il Metodo 1 (Diagonali). È il metodo più semplice e diretto.
• Se conosciamo la lunghezza di un lato e l'altezza: Utilizza il Metodo 2 (Lato e Altezza). È un metodo efficace se queste informazioni sono facilmente accessibili.
• Se conosciamo la lunghezza di un lato e l'angolo tra due lati adiacenti: Utilizza il Metodo 3 (Trigonometria). È utile quando sono disponibili informazioni angolari.

In alcuni casi, potrebbe essere necessario ricorrere a calcoli preliminari per determinare le informazioni necessarie. Ad esempio, se conosciamo solo la lunghezza di un lato e un angolo, potremmo dover utilizzare la trigonometria per calcolare l'altezza prima di applicare il Metodo 2.

Consigli e Trucchi Utili

• Verifica le Unità di Misura: Assicurati che tutte le misure siano espresse nella stessa unità di misura prima di effettuare i calcoli. Se necessario, converti le unità per evitare errori.
• Disegna un Diagramma: Disegnare un diagramma del rombo può aiutarti a visualizzare il problema e a identificare le informazioni necessarie.
• Controlla i Risultati: Dopo aver calcolato l'area, controlla se il risultato ottenuto è ragionevole. Ad esempio, l'area non può essere negativa o eccessivamente grande rispetto alle dimensioni del rombo.
• Utilizza una Calcolatrice: Per calcoli più complessi, come quelli che coinvolgono la trigonometria, utilizza una calcolatrice scientifica per ottenere risultati accurati.

Conclusione

Congratulazioni! Ora sei in grado di calcolare l'area di un rombo utilizzando diversi metodi. Ricorda, la geometria non è solo un insieme di formule, ma uno strumento potente per comprendere il mondo che ci circonda. Sperimenta, esplora e non aver paura di fare errori: l'apprendimento è un viaggio continuo. Che tu stia risolvendo un problema di matematica, progettando un nuovo pavimento o semplicemente ammirando la bellezza delle forme geometriche, la conoscenza dell'area del rombo ti sarà sicuramente utile. Ora, vai e metti in pratica le tue nuove competenze!