Come Si Trasformano Le Frazioni In Numeri Decimali

Capita a tutti noi, prima o poi, di trovarci di fronte a una frazione e di domandarci: "Come la trasformo in un numero decimale?". Magari stiamo cucinando e una ricetta ci chiede mezzo bicchiere di qualcosa, oppure dobbiamo dividere un conto tra amici e ci troviamo di fronte a un terzo del totale. La conversione da frazione a decimale è un'abilità fondamentale, non solo in matematica, ma anche nella vita di tutti i giorni. Se ti sei mai sentito frustrato o confuso di fronte a questo problema, sappi che non sei solo. Molti trovano la conversione frazioni-decimali un ostacolo, ma con la giusta guida, può diventare un'operazione semplice e intuitiva.

Perché è Importante Saperlo Fare?

La conversione frazione-decimale è più di un semplice esercizio di matematica. Ha implicazioni reali e concrete nella nostra quotidianità. Pensa a:

• Cucina: Molte ricette usano frazioni (es. 1/4 di tazza, 1/2 cucchiaino). Tradurle in decimali facilita la misurazione, soprattutto con strumenti digitali.
• Finanze: Calcolare sconti (es. 20% = 1/5) o dividere conti tra amici richiede spesso la conversione in decimali per una precisione maggiore.
• Lavoro: In molti settori, come l'edilizia o l'ingegneria, le misure sono espresse sia in frazioni che in decimali. Saper convertire velocemente è cruciale per evitare errori.
• Acquisti: Comparare prezzi unitari (es. prezzo per kg) spesso richiede di lavorare con decimali, derivati da frazioni (es. prezzo al mezzo kg).

In sostanza, la capacità di convertire frazioni in decimali ci rende più efficienti e precisi in molte situazioni.

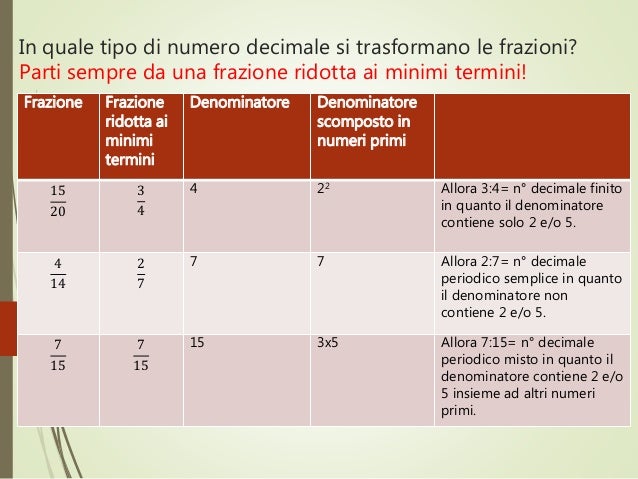
Come Convertire una Frazione in un Numero Decimale: Il Metodo Fondamentale

Il metodo più diretto per convertire una frazione in un numero decimale è la divisione. Devi semplicemente dividere il numeratore (il numero sopra la linea di frazione) per il denominatore (il numero sotto la linea di frazione).

Esempio Semplice: 1/2

Per convertire 1/2 in decimale, dividiamo 1 per 2. Il risultato è 0.5. Quindi, 1/2 = 0.5.

Esempio un po' più complesso: 3/4

Dividiamo 3 per 4. Il risultato è 0.75. Quindi, 3/4 = 0.75.

Questo metodo funziona per tutte le frazioni, anche quelle con denominatori grandi o numeratori superiori al denominatore (frazioni improprie).

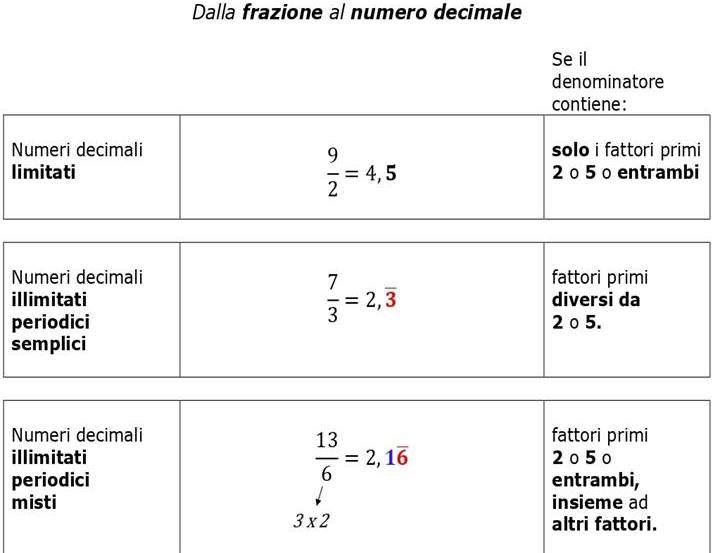
Cosa Fare con le Frazioni che Danno Decimali Infiniti Periodici?

A volte, quando dividiamo il numeratore per il denominatore, otteniamo un decimale che si ripete all'infinito, chiamato decimale periodico. Ad esempio, 1/3 = 0.3333... (il 3 si ripete all'infinito).

Come Gestire i Decimali Periodici

• Troncamento: Possiamo troncare il decimale a una certa cifra significativa. Ad esempio, possiamo approssimare 0.3333... a 0.33.
• Arrotondamento: Possiamo arrotondare il decimale. Ad esempio, se vogliamo arrotondare 0.3333... a due cifre decimali, otteniamo 0.33 (arrotondamento per difetto) oppure 0.3 (arrotondamento per eccesso, se la cifra successiva fosse 5 o superiore).
• Utilizzo della Notazione: Possiamo utilizzare la notazione per decimali periodici, indicando la parte che si ripete con una linea sopra (es. 0.3 per 0.3333...).

La scelta tra troncamento e arrotondamento dipende dal contesto e dal livello di precisione richiesto.

Trucchi e Scorciatoie Utili

Esistono alcuni trucchi e scorciatoie che possono semplificare la conversione di alcune frazioni in decimali.

Frazioni con Denominatore 10, 100, 1000, ecc.

Le frazioni con denominatore 10, 100, 1000, ecc. sono facili da convertire in decimali. Basta spostare la virgola del numeratore di tanti posti quanti sono gli zeri nel denominatore.

• 7/10 = 0.7 (un solo zero nel denominatore, spostiamo la virgola di un posto a sinistra)
• 25/100 = 0.25 (due zeri nel denominatore, spostiamo la virgola di due posti a sinistra)
• 135/1000 = 0.135 (tre zeri nel denominatore, spostiamo la virgola di tre posti a sinistra)

Frazioni che si Possono Semplificare a Denominatori Facili

A volte, possiamo semplificare una frazione in modo da ottenere un denominatore facile da convertire (es. 10, 100, 1000). Ad esempio, 2/5 può essere moltiplicata sia il numeratore che il denominatore per 2, ottenendo 4/10 = 0.4.

Riconoscere Frazioni Comuni

Con la pratica, impari a riconoscere alcune frazioni comuni e i loro equivalenti decimali. Questo ti farà risparmiare tempo e fatica. Alcuni esempi:

• 1/2 = 0.5
• 1/4 = 0.25
• 3/4 = 0.75
• 1/5 = 0.2
• 2/5 = 0.4
• 3/5 = 0.6
• 4/5 = 0.8
• 1/10 = 0.1

Affrontare le Difficoltà Comuni

Alcune persone trovano difficile la divisione lunga, soprattutto con numeri grandi. In questo caso, può essere utile utilizzare una calcolatrice. Tuttavia, è importante capire il concetto dietro la divisione, non solo premere pulsanti a caso.

Un'altra difficoltà può essere la gestione dei decimali periodici. Ricorda che in molti casi, un'approssimazione è sufficiente. Non è sempre necessario conoscere il valore esatto fino all'ultima cifra decimale.

Alcuni potrebbero sostenere che la conversione da frazione a decimale non sia così importante nell'era delle calcolatrici e dei computer. È vero che possiamo facilmente ottenere la risposta con un clic, ma comprendere il processo ci permette di sviluppare un senso numerico più forte e di prendere decisioni più informate. Inoltre, in situazioni in cui non abbiamo accesso a una calcolatrice, la capacità di convertire manualmente può essere preziosa.

Un Approccio Graduale e Continuo

Imparare a convertire frazioni in decimali è un processo graduale. Inizia con le frazioni più semplici e poi passa a quelle più complesse. Pratica regolarmente e non aver paura di chiedere aiuto se hai bisogno. Online puoi trovare tantissime risorse e esercizi che ti aiuteranno a migliorare le tue abilità.

Utilizza le frazioni e i decimali nella tua vita quotidiana. Quando fai acquisti, cucina o dividi un conto, prova a convertire le frazioni in decimali per vedere come funzionano. Questo ti aiuterà a internalizzare il processo e a renderlo più naturale.

Non scoraggiarti se commetti errori. Gli errori sono un'opportunità per imparare e migliorare. Analizza i tuoi errori e cerca di capire perché li hai commessi. Con la pratica e la perseveranza, diventerai sempre più bravo nella conversione da frazioni a decimali.

Ricorda che l'obiettivo non è solo imparare a convertire frazioni in decimali, ma anche sviluppare una maggiore comprensione dei numeri e delle loro relazioni. Questo ti aiuterà in molti altri ambiti della tua vita.

Ora, ripensa all'ultima volta che hai avuto difficoltà a convertire una frazione in decimale. Cosa avresti potuto fare di diverso? Quali strategie hai imparato oggi che potrebbero esserti utili in futuro?