Come Si Fa La Prova Del Meno

Capita a tutti, prima o poi. Ti trovi di fronte a un calcolo apparentemente perfetto, un'operazione complessa che hai rivisto più volte, ma senti che c'è qualcosa che non quadra. Forse un errore di distrazione, un segno invertito... e la frustrazione cresce. Come essere certi che il risultato sia corretto? Esiste un metodo veloce, un trucco infallibile? La risposta è sì, ed è la "Prova del Meno".

Ma prima di addentrarci nei dettagli, cerchiamo di capire perché è così importante avere a disposizione strumenti di verifica. Pensiamo a un ingegnere che progetta un ponte, a un farmacista che prepara un farmaco, a un programmatore che scrive un codice: un errore nel calcolo può avere conseguenze disastrose. La Prova del Meno, pur essendo un metodo elementare, fornisce una verifica immediata e può evitare errori potenzialmente gravi.

Cos'è la Prova del Meno?

La Prova del Meno, o prova del nove (anche se la base non è necessariamente nove, e vedremo perché), è un metodo per verificare velocemente la correttezza di un'operazione aritmetica, in particolare addizioni, sottrazioni, moltiplicazioni e divisioni. Si basa sull'aritmetica modulare, e sfrutta le proprietà dei resti della divisione per un numero scelto come modulo.

Potrebbe sembrare complicato, ma in realtà è molto semplice. Immagina di avere una pila di libri e di volerli dividere in gruppi uguali. Il numero di libri che ti avanzano dopo aver formato i gruppi è il "resto". La Prova del Meno lavora proprio con questi resti.

Come funziona?

Ecco i passaggi fondamentali:

• Scegli un modulo: Tradizionalmente si usa il 9, ma si può usare anche altri numeri primi come il 7 o l'11. La scelta del 9 rende i calcoli più semplici grazie alla sua relazione con il sistema decimale, ma ha delle limitazioni (ne parleremo più avanti).
• Calcola i resti: Per ogni numero coinvolto nell'operazione, calcola il resto della divisione per il modulo scelto. Per il 9, un trucco veloce è sommare le cifre del numero. Se il risultato è maggiore di 9, somma ancora le cifre fino a ottenere un numero compreso tra 0 e 8. Ad esempio, per il numero 1234, la somma delle cifre è 1+2+3+4 = 10. Poiché 10 è maggiore di 9, sommiamo ancora: 1+0 = 1. Quindi, il resto della divisione di 1234 per 9 è 1.
• Applica l'operazione ai resti: Esegui la stessa operazione (addizione, sottrazione, moltiplicazione o divisione) con i resti ottenuti.
• Calcola il resto del risultato: Calcola il resto della divisione per il modulo del risultato ottenuto al punto precedente.
• Verifica: Confronta questo resto con il resto della divisione per il modulo del risultato dell'operazione originale. Se i due resti coincidono, è molto probabile che l'operazione sia corretta. Attenzione: non è una garanzia assoluta, ma una forte indicazione.

Esempi pratici

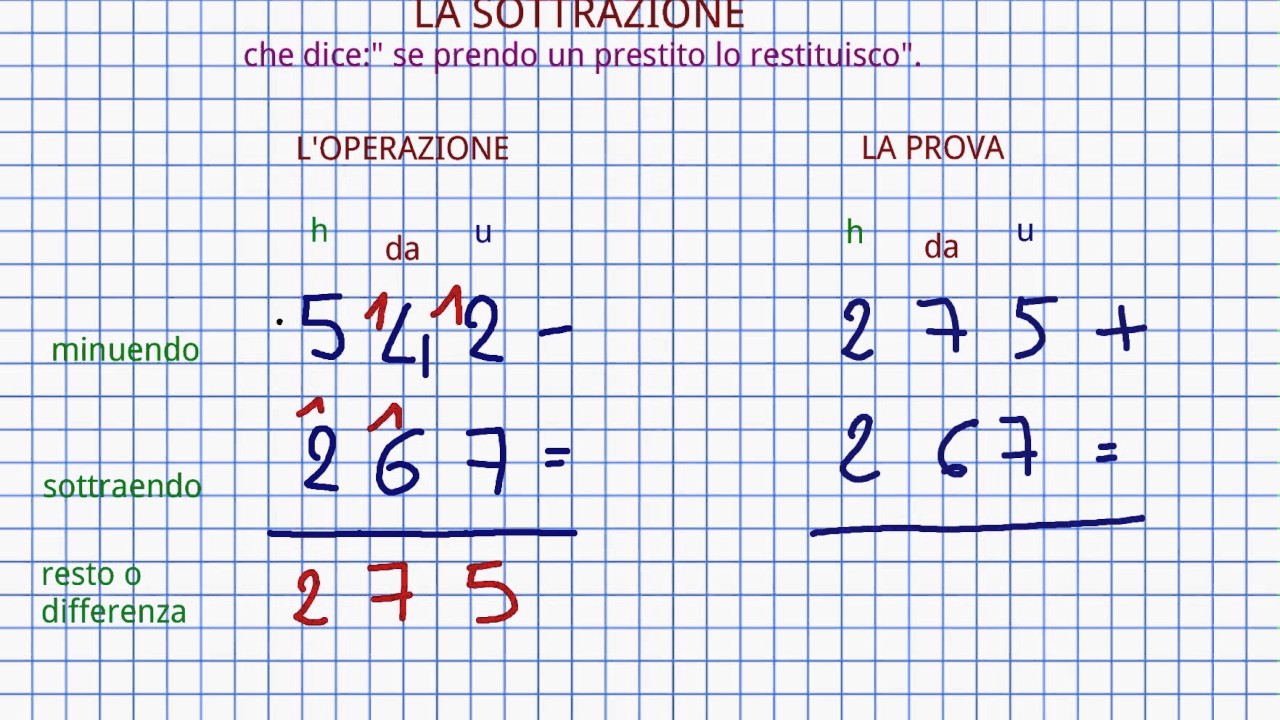
Addizione: 123 + 456 = 579

• Resto di 123 (diviso per 9): 1+2+3 = 6
• Resto di 456 (diviso per 9): 4+5+6 = 15 -> 1+5 = 6
• Somma dei resti: 6 + 6 = 12 -> 1+2 = 3
• Resto di 579 (diviso per 9): 5+7+9 = 21 -> 2+1 = 3
• I resti coincidono (3 = 3), quindi l'addizione è probabilmente corretta.

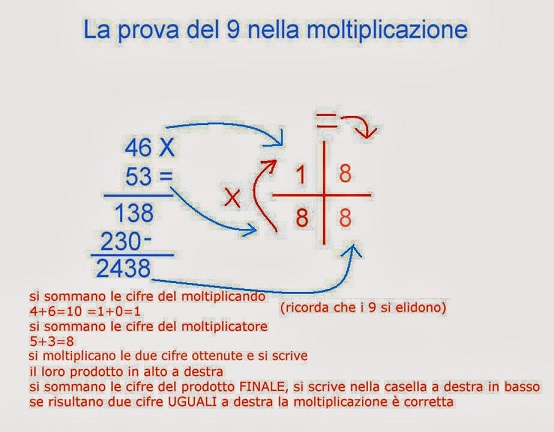
Moltiplicazione: 25 x 13 = 325

• Resto di 25 (diviso per 9): 2+5 = 7
• Resto di 13 (diviso per 9): 1+3 = 4
• Prodotto dei resti: 7 x 4 = 28 -> 2+8 = 10 -> 1+0 = 1
• Resto di 325 (diviso per 9): 3+2+5 = 10 -> 1+0 = 1
• I resti coincidono (1 = 1), quindi la moltiplicazione è probabilmente corretta.

Quando la Prova del Meno fallisce?

Come accennato, la Prova del Meno non è infallibile. Ecco alcune situazioni in cui può dare un risultato errato (un falso positivo):

• Errori che si compensano: Se si scambiano due cifre nel risultato, o se si commettono errori che si annullano a vicenda, la Prova del Meno potrebbe non rilevare l'errore. Ad esempio, se invece di 325 scrivessi 352, la somma delle cifre sarebbe comunque 10, e il resto sarebbe 1.
• Utilizzo del modulo 9: L'utilizzo del 9 come modulo ha un problema: se il risultato è sbagliato per un multiplo di 9 (ad esempio, se il risultato corretto è 325 e si scrive 334, che differisce di 9), la Prova del Meno non lo rileva. Per questo, a volte è consigliabile utilizzare altri numeri primi come modulo (7 o 11).

Critiche e Alternative

Alcuni critici della Prova del Meno sottolineano che, pur essendo un metodo veloce, non è sufficientemente affidabile per situazioni in cui la precisione è fondamentale. Inoltre, la sua efficacia diminuisce con operazioni complesse che coinvolgono un gran numero di cifre.

Un'alternativa più robusta è la verifica con la calcolatrice. Tuttavia, la Prova del Meno rimane utile per un controllo rapido "a occhio", specialmente in contesti in cui non si ha accesso a strumenti elettronici.

Un altro approccio è quello di stimare l'ordine di grandezza del risultato prima di eseguire l'operazione. Ad esempio, se devo moltiplicare 19 per 31, so che il risultato sarà approssimativamente 20 x 30 = 600. Se ottengo un risultato molto diverso (ad esempio, 60), so che ho commesso un errore.

L'importanza della comprensione, non solo della memorizzazione

È cruciale capire il perché la Prova del Meno funziona, piuttosto che limitarsi a memorizzare i passaggi. La comprensione dei principi matematici sottostanti (l'aritmetica modulare) non solo rende il metodo più efficace, ma rafforza anche la capacità di problem solving e di pensiero critico.

Conclusione

La Prova del Meno è uno strumento semplice ma utile per verificare la correttezza di operazioni aritmetiche. Pur non essendo infallibile, offre un controllo rapido e può aiutare a individuare errori grossolani. È particolarmente utile in contesti in cui la precisione è importante ma non si ha accesso a strumenti di calcolo avanzati. Ricorda, però, che la comprensione è la chiave: capire il perché il metodo funziona è più importante che memorizzare i passaggi.

Ora, prova ad applicare la Prova del Meno a qualche calcolo che hai fatto di recente. Hai scoperto qualche errore che ti era sfuggito? E, cosa più importante, ti senti più sicuro della tua capacità di verificare i tuoi risultati?