Come Si Calcola Mcd E Mcm

Ti sei mai chiesto come fare a semplificare una frazione enorme o come organizzare eventi con frequenze diverse in modo che coincidano perfettamente? La risposta a queste domande, e a molte altre in matematica e nella vita di tutti i giorni, si trova nel calcolo del Massimo Comun Divisore (MCD) e del Minimo Comune Multiplo (mcm). Questo articolo è pensato per studenti, appassionati di matematica e chiunque voglia rispolverare concetti fondamentali per risolvere problemi pratici. Cercheremo di rendere il tutto il più chiaro e intuitivo possibile.

Cos'è il Massimo Comun Divisore (MCD)?

Il MCD di due o più numeri interi è il più grande numero intero che li divide entrambi (o tutti, se sono più di due) senza lasciare resto. In parole povere, è il divisore comune più grande. Ad esempio, il MCD di 12 e 18 è 6, perché 6 è il numero più grande che divide sia 12 che 18 esattamente.

Perché è importante il MCD?

Il MCD è uno strumento potente che ci aiuta a:

• Semplificare le frazioni: Dividendo numeratore e denominatore di una frazione per il loro MCD, otteniamo la frazione equivalente più semplice possibile.
• Risolvere problemi di divisione: Immagina di avere 24 biscotti e 36 caramelle e di voler creare dei pacchetti regalo identici, contenenti sia biscotti che caramelle, usando tutti i dolci. Il MCD di 24 e 36 (che è 12) ti dice che puoi fare 12 pacchetti, ognuno con 2 biscotti e 3 caramelle.
• Ottimizzare la disposizione di oggetti: Se devi disporre oggetti rettangolari in una griglia, il MCD ti aiuta a trovare le dimensioni del quadrato più grande che puoi usare per piastrellare perfettamente l'area.

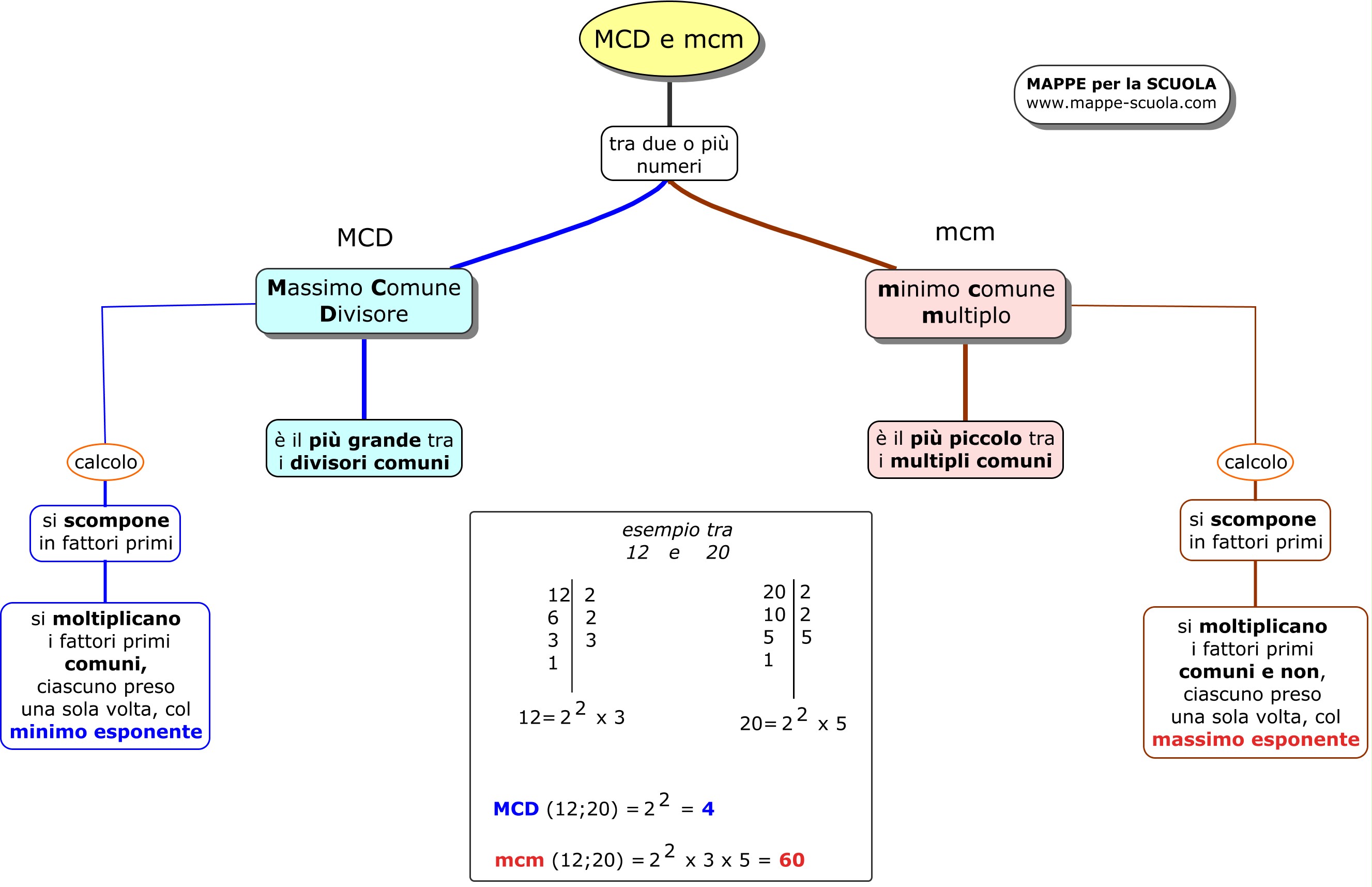
Come calcolare il MCD: Metodo della fattorizzazione

Il metodo della fattorizzazione è uno dei modi più comuni per calcolare il MCD. Ecco i passaggi:

1. Fattorizza ogni numero nei suoi fattori primi: Un fattore primo è un numero primo (come 2, 3, 5, 7, 11...) che divide il numero senza lasciare resto. Ad esempio, 12 = 2 x 2 x 3 e 18 = 2 x 3 x 3.
2. Identifica i fattori primi comuni a tutti i numeri: Nell'esempio di 12 e 18, i fattori primi comuni sono 2 e 3.
3. Prendi ogni fattore primo comune con l'esponente più piccolo: In questo caso, 2 compare con esponente 1 in entrambe le fattorizzazioni, e 3 compare con esponente 1 in quella di 12 e con esponente 2 in quella di 18. Quindi prendiamo 2¹ e 3¹.
4. Moltiplica i fattori primi comuni con gli esponenti più piccoli: 2¹ x 3¹ = 2 x 3 = 6. Quindi, il MCD di 12 e 18 è 6.

Esempio pratico: Calcoliamo il MCD di 36 e 48.

• Fattorizzazione di 36: 2 x 2 x 3 x 3 = 2² x 3²
• Fattorizzazione di 48: 2 x 2 x 2 x 2 x 3 = 2⁴ x 3¹
• Fattori primi comuni: 2 e 3
• Esponenti più piccoli: 2² e 3¹
• MCD(36, 48) = 2² x 3¹ = 4 x 3 = 12

Come calcolare il MCD: Algoritmo di Euclide

L'algoritmo di Euclide è un metodo più efficiente, soprattutto per numeri grandi. Si basa su una serie di divisioni successive. Ecco come funziona:

1. Dividi il numero più grande per il numero più piccolo: Prendi 48 e 36 dell'esempio precedente. 48 / 36 = 1 con resto di 12.
2. Sostituisci il numero più grande con il numero più piccolo e il numero più piccolo con il resto: Ora abbiamo 36 e 12.
3. Ripeti il processo finché il resto non è zero: 36 / 12 = 3 con resto di 0.
4. L'ultimo divisore (il numero più piccolo prima del resto zero) è il MCD: In questo caso, 12 è l'ultimo divisore, quindi il MCD di 36 e 48 è 12.

L'algoritmo di Euclide è particolarmente utile quando la fattorizzazione diventa difficile.

Cos'è il Minimo Comune Multiplo (mcm)?

Il mcm di due o più numeri interi è il più piccolo numero intero che è un multiplo di tutti i numeri dati. In altre parole, è il numero più piccolo che può essere diviso per ciascuno dei numeri senza lasciare resto. Ad esempio, il mcm di 4 e 6 è 12, perché 12 è il numero più piccolo divisibile sia per 4 che per 6.

Perché è importante il mcm?

Il mcm è cruciale per:

• Sommare o sottrarre frazioni con denominatori diversi: Per sommare 1/4 + 1/6, dobbiamo trovare un denominatore comune. Il mcm di 4 e 6 (che è 12) è il denominatore comune più piccolo e quindi più conveniente. Avremo quindi 3/12 + 2/12.
• Pianificare eventi ricorrenti: Immagina che un autobus passi ogni 15 minuti e un altro ogni 20 minuti. Il mcm di 15 e 20 (che è 60) ti dice che i due autobus passeranno contemporaneamente ogni 60 minuti.
• Risolvere problemi di ingranaggi: Se hai due ingranaggi con un certo numero di denti, il mcm ti aiuta a capire quante rotazioni devono fare per tornare alla posizione originale.

Come calcolare il mcm: Metodo della fattorizzazione

Come per il MCD, la fattorizzazione è un metodo efficace per trovare il mcm. Ecco i passaggi:

1. Fattorizza ogni numero nei suoi fattori primi: Usiamo di nuovo 4 e 6. 4 = 2 x 2 = 2² e 6 = 2 x 3.
2. Identifica tutti i fattori primi che compaiono in almeno una delle fattorizzazioni: In questo caso, i fattori primi sono 2 e 3.
3. Prendi ogni fattore primo con l'esponente più grande che compare in una qualsiasi delle fattorizzazioni: 2 compare con esponente 2 in 4 (2²) e con esponente 1 in 6 (2¹). Quindi prendiamo 2². 3 compare solo in 6, quindi prendiamo 3¹.
4. Moltiplica i fattori primi con gli esponenti più grandi: 2² x 3¹ = 4 x 3 = 12. Quindi, il mcm di 4 e 6 è 12.

Esempio pratico: Calcoliamo il mcm di 12 e 15.

• Fattorizzazione di 12: 2 x 2 x 3 = 2² x 3¹
• Fattorizzazione di 15: 3 x 5 = 3¹ x 5¹
• Fattori primi che compaiono: 2, 3, 5
• Esponenti più grandi: 2², 3¹, 5¹
• mcm(12, 15) = 2² x 3¹ x 5¹ = 4 x 3 x 5 = 60

Come calcolare il mcm: Usando il MCD

Esiste una relazione utile tra il MCD e il mcm: per due numeri *a* e *b*, vale la seguente formula:

mcm(*a*, *b*) = (|*a* x *b*|) / MCD(*a*, *b*)

Questo significa che se conosci il MCD di due numeri, puoi calcolare facilmente il loro mcm. Ad esempio, abbiamo già calcolato che il MCD di 36 e 48 è 12. Quindi, il mcm di 36 e 48 è (36 x 48) / 12 = 1728 / 12 = 144.

Un esempio concreto: Pianificare una festa!

Immagina di organizzare una festa e di voler servire sia pizza che patatine. La pizza è tagliata in 12 fette e il pacco di patatine contiene 18 porzioni. Vuoi che ogni ospite riceva lo stesso numero di fette di pizza e di porzioni di patatine, senza che ne avanzino. Quanti ospiti puoi invitare al massimo?

Questo è un problema di MCD! Dobbiamo trovare il MCD di 12 e 18, che abbiamo già calcolato essere 6. Quindi, puoi invitare al massimo 6 ospiti. Ogni ospite riceverà 2 fette di pizza (12 / 6 = 2) e 3 porzioni di patatine (18 / 6 = 3).

MCD e mcm: Un'accoppiata vincente

Comprendere il MCD e il mcm non è solo un esercizio di matematica; è un modo per sviluppare il pensiero logico e la capacità di risolvere problemi in modo efficiente. Che tu stia semplificando frazioni, organizzando eventi o semplicemente cercando di capire come dividere equamente delle risorse, questi concetti ti saranno di grande aiuto.

Speriamo che questo articolo ti abbia fornito una chiara comprensione di come calcolare il MCD e il mcm. Ricorda, la pratica rende perfetti! Prova a risolvere diversi esercizi e vedrai che presto questi concetti diventeranno naturali per te.