Come Si Calcola L'ipotenusa In Un Triangolo Rettangolo

In matematica, e in particolare in geometria, il triangolo rettangolo occupa un posto di rilievo. La sua semplicità apparente nasconde una profonda ricchezza di proprietà e applicazioni. Una delle caratteristiche fondamentali di questo tipo di triangolo è la presenza dell'ipotenusa, il lato più lungo che si oppone all'angolo retto (l'angolo di 90 gradi). Calcolare la lunghezza dell'ipotenusa è un'abilità essenziale, e fortunatamente esiste un metodo preciso e ben definito per farlo: il Teorema di Pitagora.

Il Teorema di Pitagora: la Chiave per Calcolare l'Ipotenusa

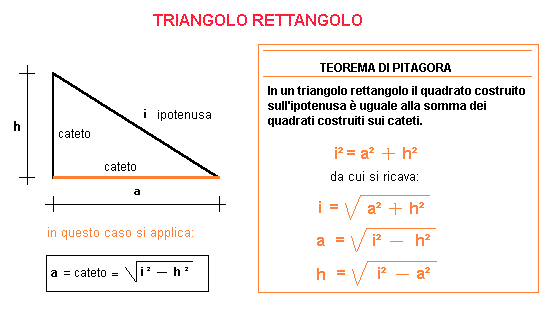
Il Teorema di Pitagora è uno dei pilastri della geometria euclidea. Afferma che, in un triangolo rettangolo, l'area del quadrato costruito sull'ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui cateti (i due lati che formano l'angolo retto). Tradotto in termini di lunghezza dei lati, questo significa:

a² + b² = c²

Dove:

• a e b rappresentano la lunghezza dei cateti.
• c rappresenta la lunghezza dell'ipotenusa.

Quindi, per calcolare l'ipotenusa (c), dobbiamo semplicemente isolare c nell'equazione. Prendiamo la radice quadrata di entrambi i lati dell'equazione:

c = √(a² + b²)

Passaggi per il Calcolo: Un Esempio Pratico

Vediamo un esempio concreto per chiarire il processo:

Supponiamo di avere un triangolo rettangolo con i cateti che misurano 3 cm e 4 cm rispettivamente. Vogliamo trovare la lunghezza dell'ipotenusa.

1. Identificare i valori: a = 3 cm, b = 4 cm
2. Applicare il Teorema di Pitagora: c² = 3² + 4²
3. Calcolare i quadrati: c² = 9 + 16
4. Sommare i risultati: c² = 25
5. Estrarre la radice quadrata: c = √25
6. Ottenere il risultato: c = 5 cm

Quindi, la lunghezza dell'ipotenusa è di 5 cm.

Perché Funziona? Una Breve Spiegazione Geometrica

Il Teorema di Pitagora non è solo una formula, ma una verità geometrica. Esistono numerose dimostrazioni visive che illustrano perché funziona. Una delle più comuni consiste nel disegnare un quadrato con lato (a + b). All'interno di questo quadrato, si possono disporre quattro triangoli rettangoli identici con lati a, b e c, lasciando al centro un quadrato con lato c. Alternativamente, si possono disporre gli stessi quattro triangoli in modo da lasciare al centro due quadrati, uno con lato a e l'altro con lato b. L'area del quadrato grande (a + b)² è la stessa in entrambi i casi. Di conseguenza, l'area del quadrato con lato c deve essere uguale alla somma delle aree dei due quadrati con lati a e b, dimostrando che a² + b² = c².

Applicazioni Pratiche nel Mondo Reale

Il calcolo dell'ipotenusa non è solo un esercizio teorico. Trova applicazione in numerosi campi professionali e situazioni quotidiane:

• Edilizia e Architettura: Gli architetti e gli ingegneri edili utilizzano il Teorema di Pitagora per assicurarsi che gli edifici siano costruiti con angoli retti perfetti. Calcolano la lunghezza diagonale di una stanza o di un terreno per garantire la precisione delle misure. Ad esempio, per verificare che un angolo di un edificio sia veramente di 90 gradi, possono misurare i due lati adiacenti (cateti) e poi confrontare la lunghezza dell'ipotenusa misurata con quella calcolata usando il teorema.
• Navigazione e Cartografia: I navigatori usano il Teorema di Pitagora per calcolare la distanza più breve tra due punti, tenendo conto della curvatura della Terra (anche se in questo caso si utilizzano versioni più complesse del teorema che considerano la geometria sferica). I cartografi lo usano per misurare le distanze e le pendenze su mappe e terreni.
• Falegnameria e Bricolage: I falegnami lo usano per tagliare il legno con precisione, costruire strutture ad angolo retto e creare diagonali perfette. Un hobbista può usare il teorema per costruire una rampa per disabili, calcolando la lunghezza necessaria per rispettare una determinata pendenza.
• Ingegneria: Gli ingegneri lo utilizzano in una vasta gamma di applicazioni, dalla progettazione di ponti e torri alla creazione di circuiti elettrici. Per esempio, possono calcolare la forza risultante di due forze perpendicolari usando il teorema.
• Grafica e Animazione: Nella grafica computerizzata e nell'animazione, il Teorema di Pitagora è usato per calcolare le distanze tra punti nello spazio 3D, cruciale per rendering, simulazioni e animazioni realistiche.

Ad esempio, se un costruttore deve costruire una rampa con una base di 12 metri e un'altezza di 5 metri, può calcolare la lunghezza della rampa (l'ipotenusa) utilizzando il Teorema di Pitagora: √(12² + 5²) = √(144 + 25) = √169 = 13 metri. Quindi, la rampa dovrà essere lunga 13 metri.

Attenzione agli Errori Comuni

Nonostante la sua semplicità, è facile commettere errori nell'applicazione del Teorema di Pitagora. Ecco alcuni errori comuni da evitare:

• Confondere i lati: Assicurarsi di identificare correttamente l'ipotenusa (il lato opposto all'angolo retto) e i cateti.
• Applicare il teorema a triangoli non rettangoli: Il Teorema di Pitagora si applica solo ai triangoli rettangoli. Non è valido per triangoli acutangoli o ottusangoli.
• Dimenticare di estrarre la radice quadrata: Dopo aver calcolato c², non dimenticare di estrarre la radice quadrata per ottenere c (la lunghezza dell'ipotenusa).
• Errori di calcolo: Prestare attenzione ai calcoli, soprattutto quando si elevano al quadrato i numeri. Un piccolo errore può portare a un risultato completamente sbagliato.

Oltre il Teorema: Trigonometria

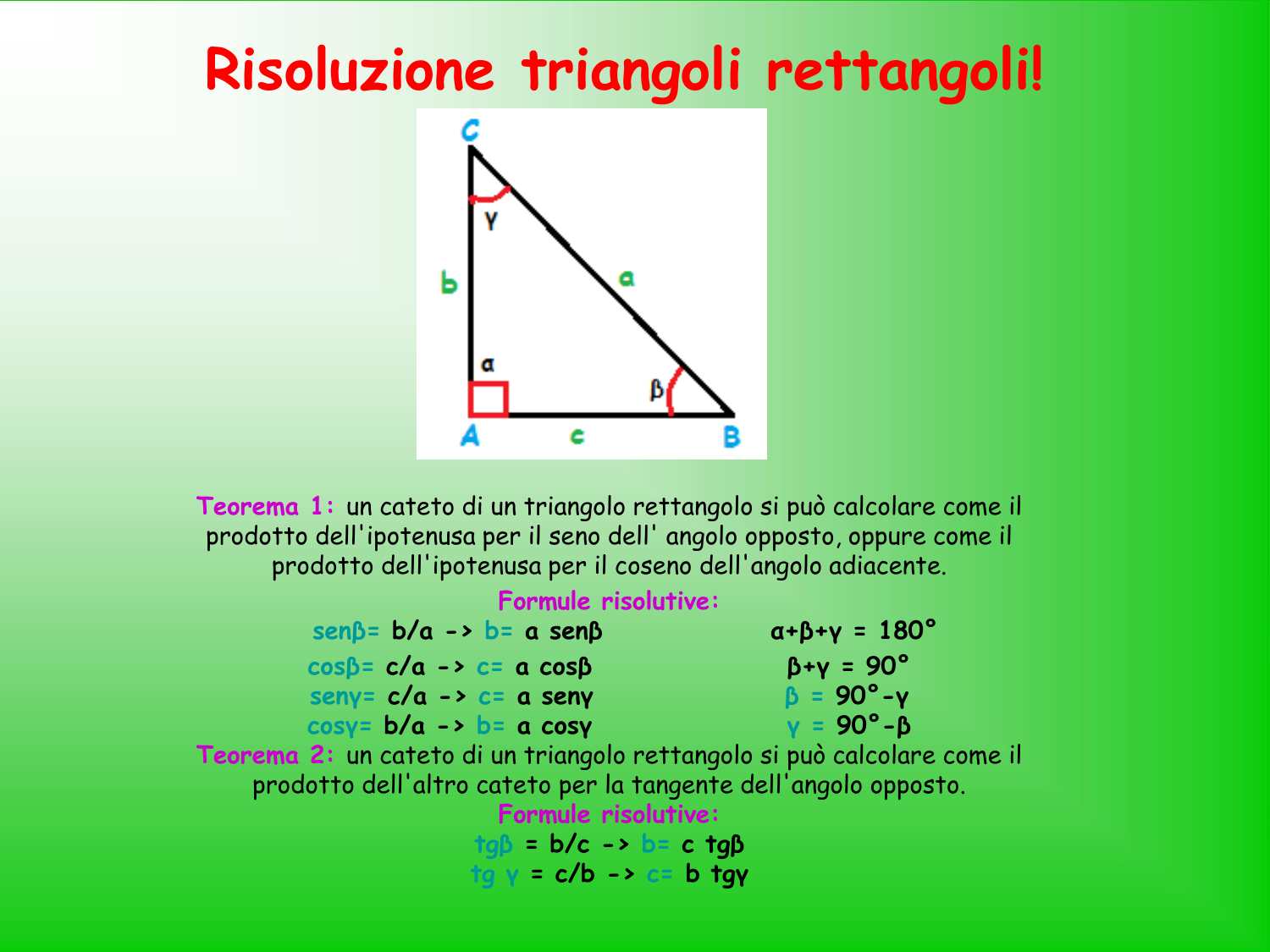
Il Teorema di Pitagora è un punto di partenza per lo studio della trigonometria. La trigonometria è un ramo della matematica che studia le relazioni tra gli angoli e i lati dei triangoli. Le funzioni trigonometriche, come il seno, il coseno e la tangente, si basano sul Teorema di Pitagora e permettono di risolvere problemi più complessi che coinvolgono triangoli non rettangoli o angoli sconosciuti.

Ad esempio, conoscendo un angolo acuto di un triangolo rettangolo e la lunghezza di un cateto, si può utilizzare la tangente per calcolare la lunghezza dell'altro cateto.

Conclusione: Un Fondamento per la Comprensione

Il Teorema di Pitagora è molto più di una semplice formula. È un fondamento della geometria, un potente strumento che trova applicazione in una miriade di discipline. Comprendere il suo significato e saperlo applicare correttamente è essenziale per chiunque studi matematica, scienze o ingegneria.

Esercitati con diversi esempi, esplora le dimostrazioni visive e non aver paura di utilizzare questo strumento per risolvere problemi pratici. La padronanza del Teorema di Pitagora ti aprirà le porte a una comprensione più profonda del mondo che ti circonda.

Ora tocca a te! Prova a risolvere alcuni esercizi online o cerca applicazioni pratiche nella tua vita quotidiana. Scoprirai quanto è utile e versatile questo teorema.