Come Si Calcola L'ipotenusa Di Un Triangolo Rettangolo

Ti sei mai trovato di fronte a un problema di geometria che sembrava insormontabile? Magari dovevi calcolare la distanza tra due punti che non potevi misurare direttamente, oppure progettare un tetto spiovente e avevi bisogno di conoscere la lunghezza esatta delle travi. In questi casi, conoscere come calcolare l'ipotenusa di un triangolo rettangolo può essere una competenza incredibilmente utile e potente. Non preoccuparti se la matematica non è il tuo forte: cercheremo di rendere il processo il più semplice e intuitivo possibile.

Spesso, quando sentiamo parlare di "teoremi" e "formule", ci sentiamo intimiditi. Ma in realtà, dietro a questi concetti si nascondono strumenti molto pratici che possono semplificarci la vita in molti modi. Immagina di dover installare una rampa per disabili: conoscere la lunghezza dell'ipotenusa ti permetterà di calcolare l'inclinazione corretta, garantendo un accesso sicuro e confortevole. Oppure, se sei un appassionato di bricolage, potresti aver bisogno di costruire una mensola angolare: il teorema di Pitagora ti aiuterà a tagliare i pezzi di legno con la precisione necessaria.

Cos'è un Triangolo Rettangolo e l'Ipotenusa?

Prima di addentrarci nei calcoli, è fondamentale avere ben chiare le definizioni. Un triangolo rettangolo è un triangolo che ha un angolo di 90 gradi, comunemente chiamato "angolo retto". Questo angolo è spesso indicato con un piccolo quadratino nell'angolo stesso.

I lati di un triangolo rettangolo hanno nomi specifici:

I Cateti: Sono i due lati che formano l'angolo retto.
L'Ipotenusa: È il lato opposto all'angolo retto, ed è anche il lato più lungo del triangolo.

L'ipotenusa è quindi il lato "diagonale" del triangolo rettangolo. Capire cos'è e come identificarla è il primo passo per poterla calcolare.

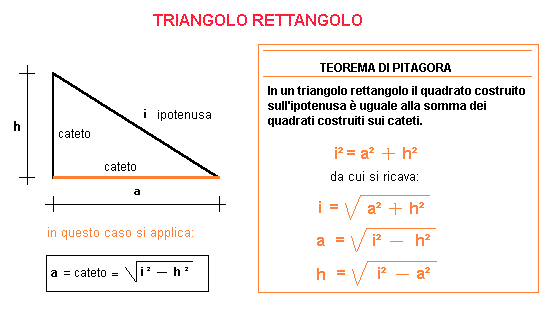
Il Teorema di Pitagora: La Chiave per Calcolare l'Ipotenusa

Il teorema di Pitagora è il pilastro fondamentale per calcolare l'ipotenusa. Questo teorema afferma che in un triangolo rettangolo, il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti. In altre parole:

a² + b² = c²

Dove:

a e b sono le lunghezze dei cateti.
c è la lunghezza dell'ipotenusa.

Questo teorema, apparentemente complesso, è in realtà molto semplice da applicare. Vediamo come.

Come Applicare il Teorema di Pitagora per Trovare l'Ipotenusa

Per calcolare l'ipotenusa, dobbiamo ricavare c dalla formula. Per farlo, prendiamo la radice quadrata di entrambi i lati dell'equazione:

c = √(a² + b²)

Questa è la formula che utilizzeremo per calcolare la lunghezza dell'ipotenusa.

Esempio Pratico:

Immagina un triangolo rettangolo con un cateto di 3 cm e un altro di 4 cm. Vogliamo calcolare la lunghezza dell'ipotenusa.

Identifica i cateti: a = 3 cm, b = 4 cm
Applica la formula: c = √(3² + 4²)
Calcola i quadrati: c = √(9 + 16)
Somma i quadrati: c = √25
Calcola la radice quadrata: c = 5 cm

Quindi, l'ipotenusa del triangolo rettangolo è di 5 cm.

E se Conosco l'Ipotenusa e un Cateto?

A volte, potresti conoscere la lunghezza dell'ipotenusa e di uno dei cateti, e voler trovare la lunghezza del cateto mancante. In questo caso, possiamo semplicemente riorganizzare il teorema di Pitagora.

Se conosciamo l'ipotenusa (c) e un cateto (a), possiamo trovare l'altro cateto (b) usando la formula:

b = √(c² - a²)

Esempio:

Supponiamo di avere un triangolo rettangolo con un'ipotenusa di 13 cm e un cateto di 5 cm. Vogliamo trovare la lunghezza dell'altro cateto.

Identifica l'ipotenusa e il cateto: c = 13 cm, a = 5 cm
Applica la formula: b = √(13² - 5²)
Calcola i quadrati: b = √(169 - 25)
Sottrai i quadrati: b = √144
Calcola la radice quadrata: b = 12 cm

Quindi, l'altro cateto è di 12 cm.

Errori Comuni da Evitare

Anche se il teorema di Pitagora è relativamente semplice, ci sono alcuni errori comuni che è bene evitare:

Confondere i cateti con l'ipotenusa: Assicurati di identificare correttamente l'ipotenusa (il lato opposto all'angolo retto) prima di applicare la formula.
Dimenticare di elevare al quadrato: Ricorda che devi elevare al quadrato le lunghezze dei cateti e dell'ipotenusa prima di sommarle o sottrarle.
Non calcolare la radice quadrata: Dopo aver sommato (o sottratto) i quadrati, non dimenticare di calcolare la radice quadrata per ottenere la lunghezza dell'ipotenusa (o del cateto).

Applicazioni Pratiche del Calcolo dell'Ipotenusa

Come abbiamo accennato all'inizio, il calcolo dell'ipotenusa ha molte applicazioni pratiche. Ecco alcuni esempi:

Edilizia e Costruzioni: Calcolo della lunghezza delle travi per tetti, scale, rampe, ecc.
Navigazione: Determinare la distanza tra due punti utilizzando le coordinate geografiche.
Ingegneria: Progettazione di ponti, strutture e altre opere civili.
Fisica: Calcolo di vettori e forze.
Grafica Computerizzata: Calcolo delle distanze tra punti in uno spazio 2D o 3D.

Questi sono solo alcuni esempi, ma le possibilità sono infinite. La capacità di calcolare l'ipotenusa è uno strumento potente che può essere applicato in molti contesti diversi.

Controindicazioni e Alternative

Sebbene il teorema di Pitagora sia un metodo efficace per calcolare l'ipotenusa, è importante ricordare che si applica solo ai triangoli rettangoli. Se hai un triangolo che non ha un angolo retto, dovrai utilizzare altri metodi, come la legge dei coseni o la legge dei seni.

Alcuni potrebbero sostenere che con l'avvento delle calcolatrici e dei software di geometria, non è più necessario conoscere il teorema di Pitagora. Tuttavia, comprendere i principi fondamentali alla base dei calcoli è essenziale per risolvere problemi complessi e per interpretare correttamente i risultati ottenuti con gli strumenti digitali. Inoltre, la capacità di eseguire calcoli mentali o su carta può essere preziosa in situazioni in cui non si ha accesso a una calcolatrice.

Riepilogo e Consigli Finali

Calcolare l'ipotenusa di un triangolo rettangolo è un'abilità fondamentale che può essere utile in molti aspetti della vita. Ricorda:

Identifica il triangolo rettangolo: Assicurati che il triangolo abbia un angolo retto.
Identifica i cateti e l'ipotenusa: Distingui chiaramente i cateti (i lati che formano l'angolo retto) dall'ipotenusa (il lato opposto all'angolo retto).
Applica il teorema di Pitagora: Usa la formula c = √(a² + b²) per calcolare l'ipotenusa.
Verifica i risultati: Assicurati che la lunghezza dell'ipotenusa sia maggiore delle lunghezze dei cateti.
Pratica, pratica, pratica: Più ti eserciti, più diventerai bravo a calcolare l'ipotenusa!

Non aver paura di sperimentare e di fare errori. L'importante è imparare dai propri errori e continuare a migliorare le proprie competenze matematiche.

Ora che hai imparato a calcolare l'ipotenusa, quali nuovi progetti o problemi vorresti affrontare con questa nuova conoscenza?