Come Si Calcola L'area Totale Di Un Parallelepipedo

Hai mai ammirato un pacco regalo perfettamente incartato, un mattone ben posizionato o persino un comune scatolone? Dietro la loro apparente semplicità si cela una forma geometrica tridimensionale chiamata parallelepipedo. Capire come calcolare l'area totale di questa figura è fondamentale in molti ambiti, dall'edilizia all'imballaggio, fino alla semplice curiosità matematica. Questa guida è pensata per te, che magari sei uno studente alle prese con la geometria, un professionista che necessita di misurazioni precise, o semplicemente una persona curiosa desiderosa di approfondire le proprie conoscenze.

Cos'è un Parallelepipedo?

Prima di addentrarci nel calcolo dell'area, definiamo cos'è esattamente un parallelepipedo. Immagina un rettangolo che viene estruso (spinto) nello spazio, mantenendo sempre la stessa forma e dimensione. Il risultato è un solido con sei facce, ognuna delle quali è un parallelogramma. Ricorda che un parallelogramma è un quadrilatero con lati opposti paralleli e uguali a due a due.

Esistono diverse tipologie di parallelepipedi:

Parallelepipedo rettangolo (o cuboide): Le sue facce sono tutti rettangoli e gli angoli diedri sono retti. Pensa a una scatola da scarpe.
Cubo: Un caso speciale del parallelepipedo rettangolo in cui tutti i lati sono uguali.
Romboedro: Le sue facce sono tutti rombi.
Parallelepipedo obliquo: Le sue facce sono parallelogrammi (non rettangoli) e gli angoli diedri non sono retti.

In questa guida, ci concentreremo principalmente sul parallelepipedo rettangolo, data la sua frequente applicazione pratica e la relativa semplicità nel calcolo dell'area.

Perché Calcolare l'Area Totale?

Il calcolo dell'area totale di un parallelepipedo è utile in una varietà di situazioni:

Imballaggio: Determinare la quantità di materiale necessario per costruire una scatola o un contenitore.
Edilizia: Calcolare la superficie di muri da rivestire o da pitturare.
Arredamento: Stimare la quantità di tessuto necessario per foderare un divano o una poltrona.
Matematica e Fisica: Risolvere problemi geometrici e fisici che coinvolgono volumi e superfici.

Immagina di dover pitturare una stanza che ha la forma di un parallelepipedo rettangolo. Calcolare l'area totale delle pareti, del soffitto e (se necessario) del pavimento ti permetterà di acquistare la giusta quantità di vernice, evitando sprechi e assicurandoti un risultato impeccabile.

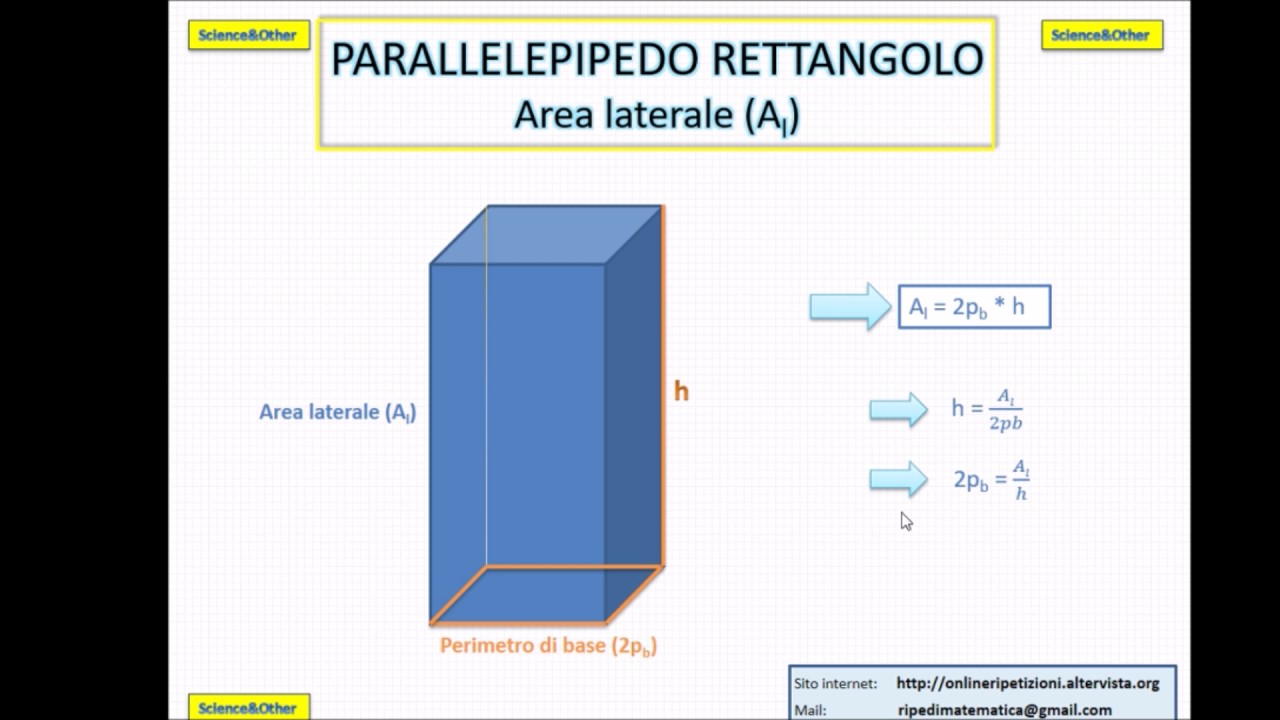
La Formula Magica: Come Calcolare l'Area Totale di un Parallelepipedo Rettangolo

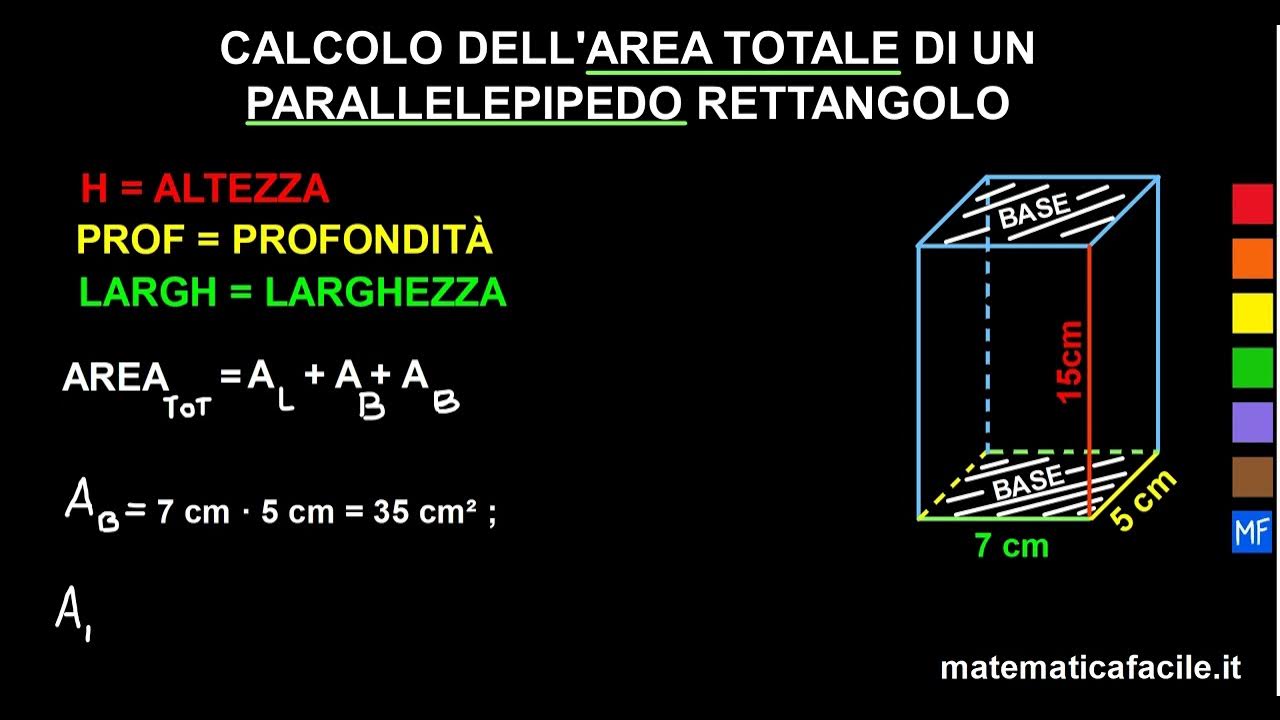
L'area totale di un parallelepipedo rettangolo è data dalla somma delle aree di tutte le sue sei facce. Poiché le facce opposte sono uguali a due a due, possiamo semplificare il calcolo utilizzando la seguente formula:

Area Totale = 2 * (lunghezza * larghezza + lunghezza * altezza + larghezza * altezza)

Dove:

lunghezza è la dimensione di uno dei lati della base.
larghezza è la dimensione dell'altro lato della base.
altezza è la distanza tra le due basi.

In termini matematici, possiamo scrivere: A = 2(lb + lh + bh) dove:

A = Area Totale
l = lunghezza
b = larghezza (breadth in inglese, da cui la 'b')
h = altezza

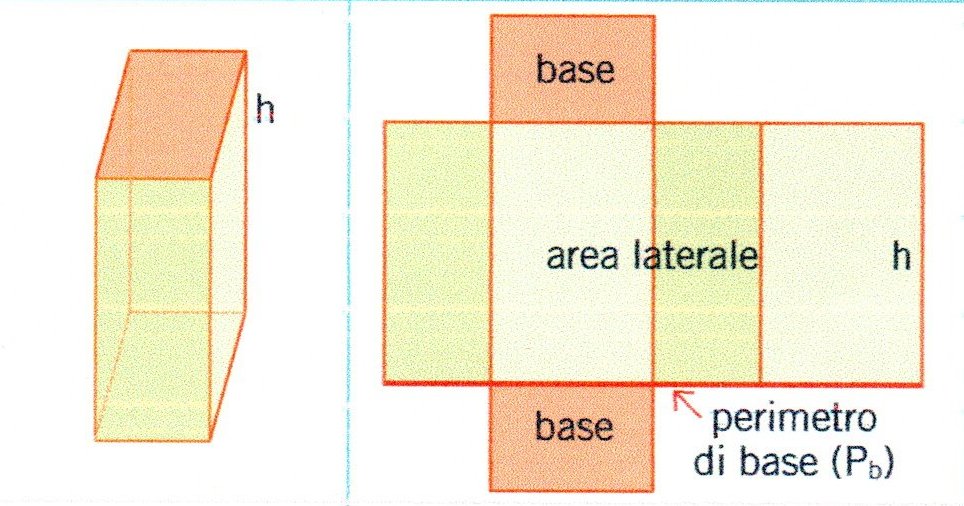
Cerchiamo di rendere la formula più intuitiva. Pensa a una scatola. Hai bisogno di calcolare l'area del fondo (lunghezza * larghezza), l'area di un lato (lunghezza * altezza) e l'area dell'altro lato (larghezza * altezza). Dato che ogni faccia ha una sua gemella opposta, moltiplichiamo la somma di queste tre aree per 2 per ottenere l'area totale.

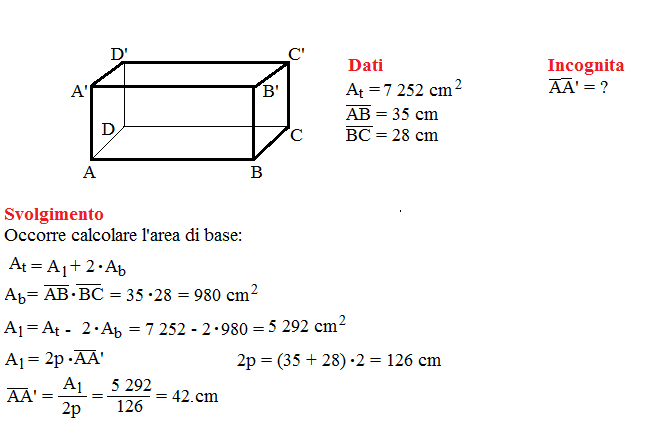
Un Esempio Pratico

Supponiamo di avere un parallelepipedo rettangolo con le seguenti dimensioni:

Lunghezza (l) = 5 cm
Larghezza (b) = 3 cm
Altezza (h) = 4 cm

Applichiamo la formula:

Area Totale = 2 * (5 cm * 3 cm + 5 cm * 4 cm + 3 cm * 4 cm)

Area Totale = 2 * (15 cm² + 20 cm² + 12 cm²)

Area Totale = 2 * (47 cm²)

Area Totale = 94 cm²

Quindi, l'area totale del nostro parallelepipedo rettangolo è di 94 centimetri quadrati.

Passaggi Semplici per il Calcolo

Misura: Determina la lunghezza, la larghezza e l'altezza del parallelepipedo rettangolo. Assicurati che tutte le misure siano nella stessa unità di misura (es. cm, metri, pollici).
Calcola le Aree delle Facce: Calcola l'area di ogni faccia utilizzando le formule appropriate (lunghezza * larghezza, lunghezza * altezza, larghezza * altezza).
Somma e Moltiplica: Somma le tre aree calcolate e moltiplica il risultato per 2.
Verifica: Ricontrolla i tuoi calcoli per evitare errori.
Unità di Misura: Esprimi il risultato finale nell'unità di misura appropriata (es. cm², m², pollici²).

Parallelepipedo Qualsiasi: Come Calcolare l'Area Totale

Se il tuo parallelepipedo non è rettangolo, il calcolo dell'area totale diventa un po' più complesso. In questo caso, devi calcolare l'area di ogni parallelogramma singolarmente e poi sommare tutte le aree.

Ricorda che l'area di un parallelogramma è data da: Area = base * altezza, dove l'altezza è la distanza perpendicolare tra la base e il lato opposto.

Quindi, i passaggi sono:

Identifica le Facce: Individua tutte e sei le facce del parallelepipedo.
Calcola l'Area di Ogni Faccia: Calcola l'area di ogni parallelogramma utilizzando la formula appropriata (base * altezza).
Somma le Aree: Somma tutte le aree calcolate per ottenere l'area totale del parallelepipedo.

Questo metodo è più laborioso, ma ti permette di calcolare l'area totale di qualsiasi parallelepipedo, indipendentemente dalla forma delle sue facce.

Strumenti Utili

Se hai difficoltà con i calcoli manuali, puoi utilizzare diversi strumenti online per semplificare il processo:

Calcolatrici Online: Esistono numerose calcolatrici online che ti permettono di inserire le dimensioni del parallelepipedo e ottenere immediatamente l'area totale.
Software di Modellazione 3D: Se hai bisogno di calcolare l'area di un parallelepipedo complesso, puoi utilizzare un software di modellazione 3D per ottenere misurazioni precise.

Questi strumenti possono essere particolarmente utili per verificare i tuoi calcoli manuali e per risparmiare tempo in progetti complessi.

Errori Comuni da Evitare

Durante il calcolo dell'area totale di un parallelepipedo, è facile commettere alcuni errori comuni. Ecco alcuni consigli per evitarli:

Unità di Misura Incoerenti: Assicurati che tutte le misure siano nella stessa unità di misura prima di iniziare i calcoli.
Confusione tra Lunghezza, Larghezza e Altezza: Identifica correttamente le dimensioni del parallelepipedo per evitare errori nella formula.
Errori di Calcolo: Ricontrolla attentamente i tuoi calcoli per evitare errori matematici.
Dimenticare di Moltiplicare per 2: Ricorda che devi moltiplicare la somma delle aree delle tre facce per 2 per ottenere l'area totale.

Prestando attenzione a questi dettagli, puoi minimizzare il rischio di errori e ottenere risultati precisi.

Conclusione

Speriamo che questa guida ti abbia fornito una comprensione chiara e completa di come calcolare l'area totale di un parallelepipedo. Che tu sia uno studente, un professionista o semplicemente una persona curiosa, questa conoscenza ti sarà utile in molte situazioni. Ricorda la formula fondamentale, presta attenzione alle unità di misura e, soprattutto, divertiti ad applicare ciò che hai imparato! Ora hai gli strumenti per affrontare qualsiasi sfida geometrica che ti si presenti, che si tratti di incartare un regalo, stimare la quantità di vernice necessaria per una stanza o semplicemente soddisfare la tua curiosità matematica. Continua ad esplorare il meraviglioso mondo della geometria e scoprirai che le forme che ci circondano nascondono segreti affascinanti e applicazioni pratiche inaspettate.