Come Si Calcola L'area Del Rombo Sapendo Le Diagonali

Il rombo, una figura geometrica affascinante con le sue proprietà uniche, è un quadrilatero equilatero, il che significa che tutti i suoi lati sono di uguale lunghezza. Tuttavia, a differenza del quadrato, i suoi angoli non sono necessariamente retti. Questa caratteristica distintiva ci porta a metodi specifici per calcolare la sua area, in particolare quando conosciamo le lunghezze delle sue diagonali. Questo articolo esplorerà in dettaglio come determinare l'area di un rombo utilizzando le sue diagonali, fornendo una spiegazione chiara e accessibile a tutti.

Comprendere il Rombo e le sue Diagonali

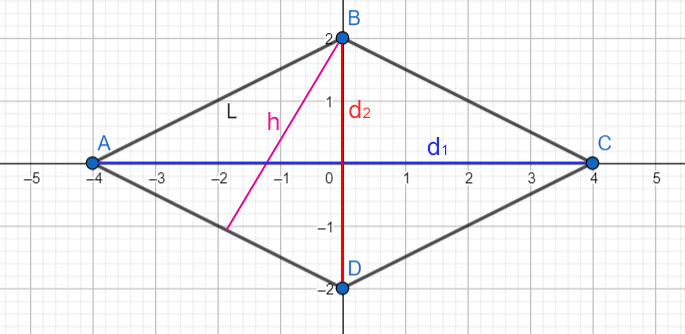
Prima di addentrarci nel calcolo dell'area, è fondamentale capire cosa sono le diagonali di un rombo. Una diagonale è un segmento di retta che congiunge due vertici non adiacenti di un poligono. Nel rombo, abbiamo due diagonali: una più lunga (diagonale maggiore) e una più corta (diagonale minore). Queste diagonali hanno una proprietà cruciale: si intersecano a metà e formano angoli retti (90 gradi) nel punto di intersezione. Questa proprietà è la chiave per comprendere la formula dell'area.

Le Proprietà Chiave delle Diagonali del Rombo

Come accennato, le diagonali del rombo presentano delle caratteristiche fondamentali che semplificano il calcolo dell'area:

* Perpendicolarità: Le diagonali si intersecano formando un angolo retto. Questo è cruciale perché ci permette di considerare il rombo come composto da quattro triangoli rettangoli congruenti. * Bisettrici: Le diagonali bisecano gli angoli ai vertici da cui partono. Questo significa che dividono l'angolo in due angoli uguali. * Punto Medio: Il punto di intersezione delle diagonali è il punto medio di entrambe le diagonali. Questo implica che ogni diagonale è divisa a metà nel punto di intersezione.

Queste proprietà, in particolare la perpendicolarità, sono essenziali per derivare e comprendere la formula dell'area.

La Formula per Calcolare l'Area del Rombo Utilizzando le Diagonali

La formula per calcolare l'area di un rombo quando si conoscono le lunghezze delle sue diagonali è sorprendentemente semplice:

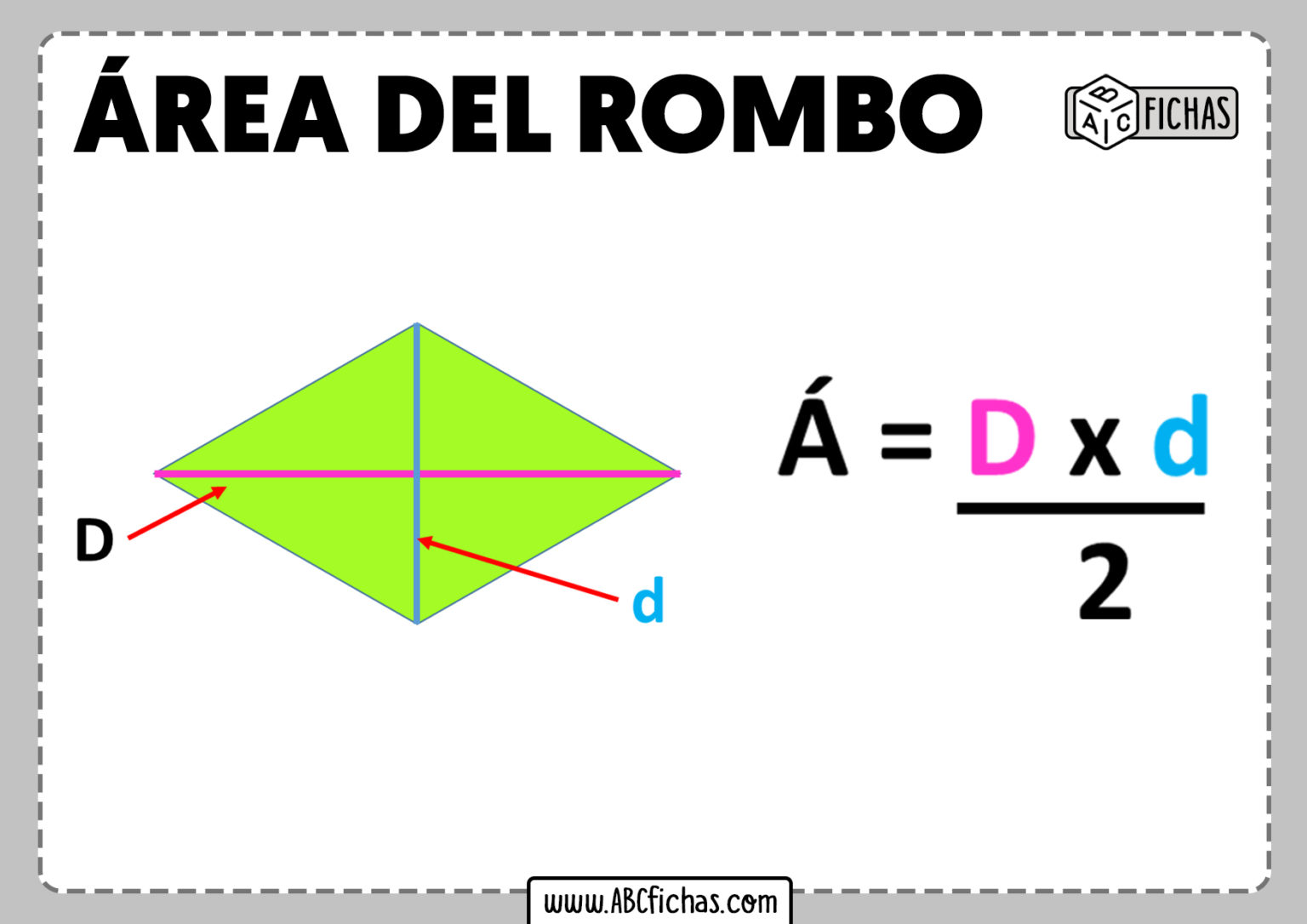
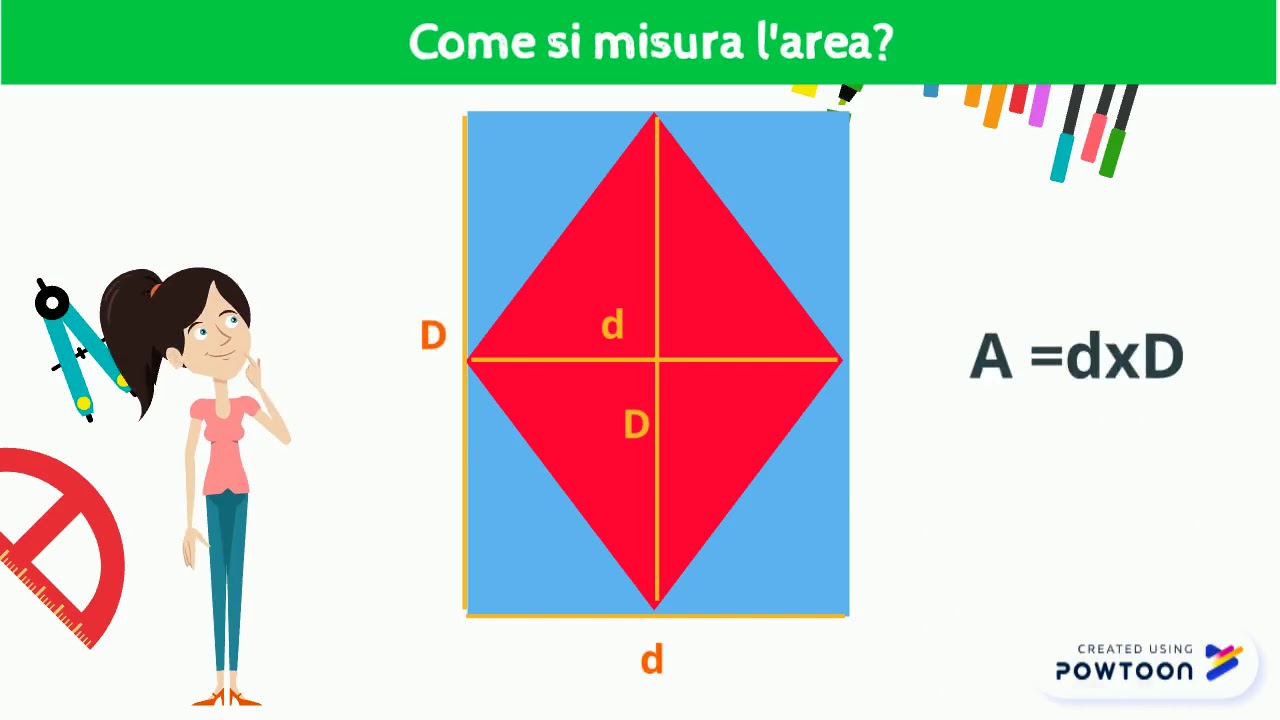
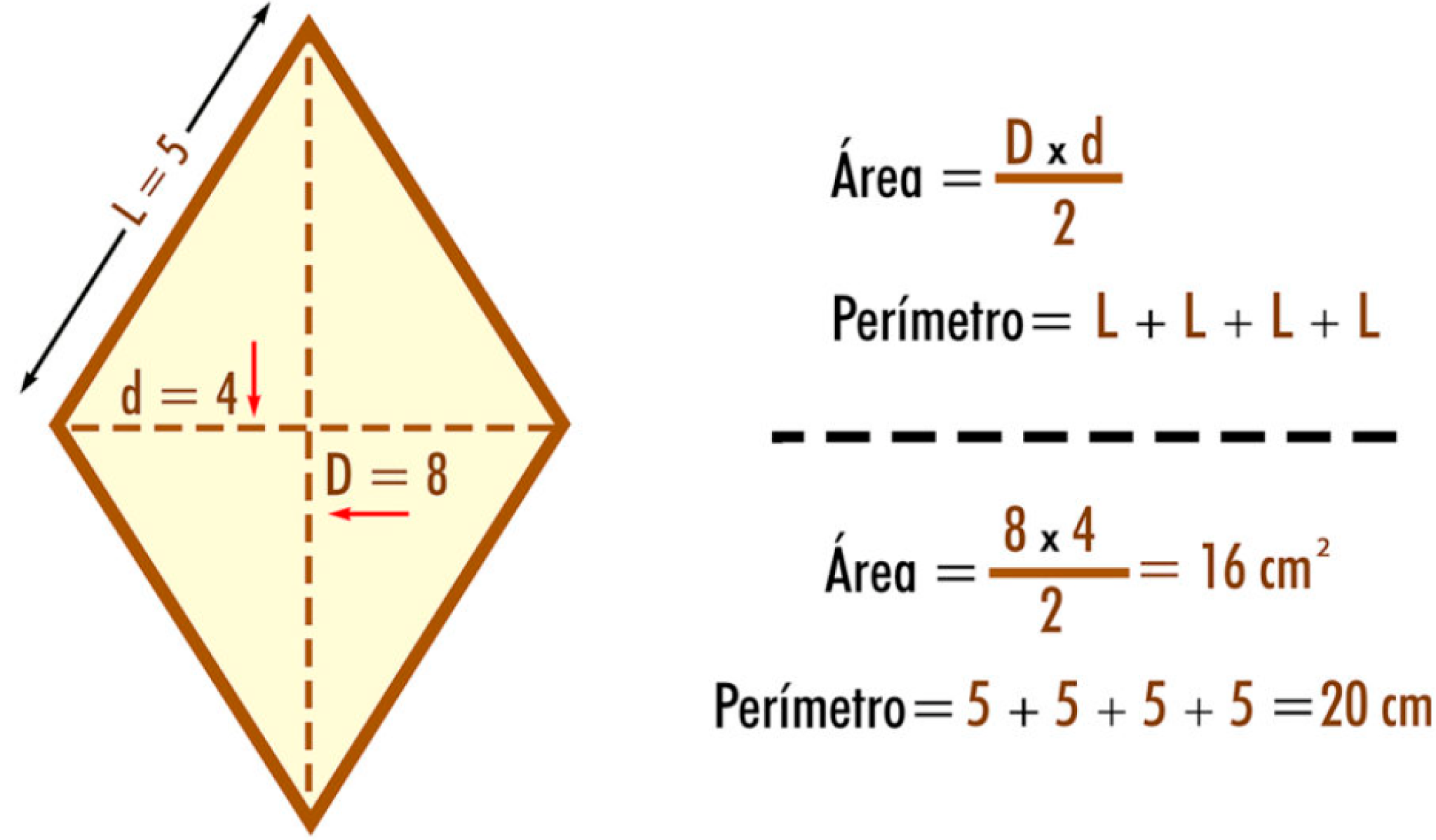
Area = (Diagonale Maggiore × Diagonale Minore) / 2

In termini matematici, se indichiamo la diagonale maggiore con D e la diagonale minore con d, la formula diventa:

Area = (D × d) / 2

Questa formula è diretta e facile da applicare. Vediamo ora perché funziona.

Derivazione della Formula

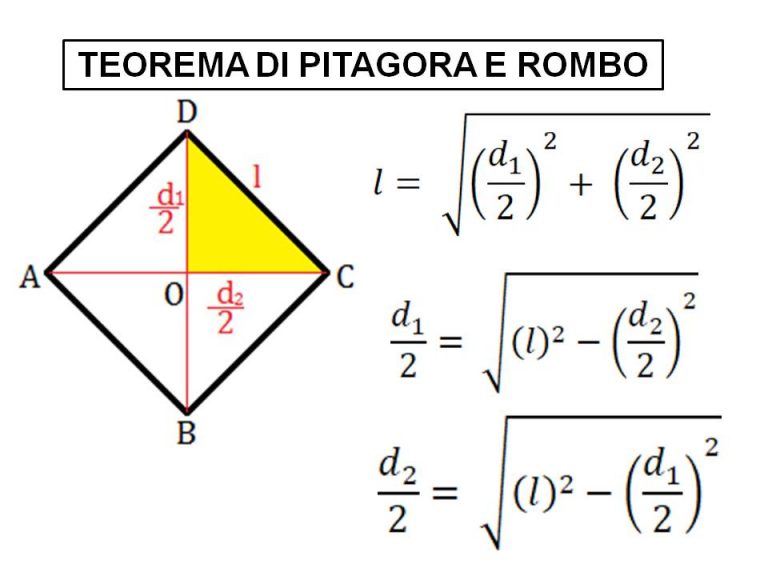
Possiamo derivare questa formula considerando il rombo come composto da quattro triangoli rettangoli congruenti. Ciascuno di questi triangoli ha una base pari alla metà della diagonale maggiore (D/2) e un'altezza pari alla metà della diagonale minore (d/2).

L'area di un singolo triangolo rettangolo è data da: (base × altezza) / 2. Quindi, l'area di uno dei nostri triangoli è: ((D/2) × (d/2)) / 2 = (D × d) / 8.

Poiché ci sono quattro triangoli congruenti, l'area totale del rombo è 4 volte l'area di un singolo triangolo: 4 × ((D × d) / 8) = (D × d) / 2. Ecco dimostrata la formula!

Esempi Pratici di Calcolo dell'Area

Per consolidare la comprensione, consideriamo alcuni esempi pratici:

Esempio 1:

Supponiamo di avere un rombo con una diagonale maggiore di 10 cm e una diagonale minore di 6 cm. Qual è la sua area?

Applicando la formula: Area = (10 cm × 6 cm) / 2 = 30 cm². Quindi, l'area del rombo è di 30 centimetri quadrati.

Esempio 2:

Un rombo ha una diagonale maggiore di 15 metri e una diagonale minore di 8 metri. Calcola l'area.

Usando la formula: Area = (15 m × 8 m) / 2 = 60 m². L'area di questo rombo è di 60 metri quadrati.

Esempio 3:

Immaginiamo di dover calcolare l'area di un aquilone a forma di rombo. Le aste che lo sostengono formano le diagonali. Se un'asta (diagonale maggiore) misura 1.2 metri e l'altra (diagonale minore) misura 0.7 metri, qual è l'area del tessuto necessario per costruirlo?

Area = (1.2 m × 0.7 m) / 2 = 0.42 m². Dunque, servono 0.42 metri quadrati di tessuto.

Applicazioni nel Mondo Reale

La capacità di calcolare l'area di un rombo ha applicazioni pratiche in vari campi:

* Architettura e Design: Molti elementi architettonici e di design incorporano forme romboidali. Conoscere l'area è essenziale per il calcolo dei materiali necessari per la costruzione o la decorazione. Pensa alle piastrelle romboidali, ai mosaici o alle facciate di edifici. * Ingegneria: In ingegneria strutturale, la comprensione delle proprietà geometriche, inclusa l'area, di diverse forme è fondamentale per il calcolo delle forze e la stabilità delle strutture. * Gioielleria: Le gemme tagliate a forma di rombo richiedono calcoli precisi per massimizzare la brillantezza e l'utilizzo del materiale grezzo. L'area della superficie influisce sulla percezione della dimensione e del valore della gemma. * Artigianato e Hobbistica: Nella realizzazione di aquiloni, origami, patchwork e altri progetti creativi, la conoscenza dell'area del rombo è utile per la pianificazione e il taglio dei materiali. * Cartografia e Geodesia: Anche se non direttamente, la comprensione delle figure geometriche è alla base di molti calcoli legati alla rappresentazione della superficie terrestre e alla misurazione delle distanze.

Un Esempio Concreto: Il Calcolo del Materiale per un Pavimento

Consideriamo un esempio più dettagliato: un architetto sta progettando un pavimento con piastrelle a forma di rombo. Ogni piastrella ha una diagonale maggiore di 30 cm e una diagonale minore di 20 cm. L'area totale del pavimento da coprire è di 15 metri quadrati. Quante piastrelle sono necessarie?

1. Calcola l'area di una piastrella: Area = (30 cm × 20 cm) / 2 = 300 cm²

2. Converti l'area totale del pavimento in centimetri quadrati: 15 m² = 15 × 10,000 cm² = 150,000 cm²

3. Dividi l'area totale del pavimento per l'area di una piastrella: 150,000 cm² / 300 cm² = 500 piastrelle

Pertanto, l'architetto avrà bisogno di 500 piastrelle per coprire l'intero pavimento.

Conclusioni e Suggerimenti

Il calcolo dell'area di un rombo conoscendo le sue diagonali è un processo semplice ed efficiente, grazie alla formula Area = (D × d) / 2. La comprensione delle proprietà geometriche del rombo, in particolare la perpendicolarità delle diagonali, è fondamentale per apprezzare la validità di questa formula.

Suggerimenti utili:

* Assicurati sempre che le unità di misura delle diagonali siano le stesse prima di effettuare il calcolo. Se una diagonale è in centimetri e l'altra in metri, converti una delle due per evitare errori. * Ricorda che la formula funziona solo se conosci le lunghezze delle diagonali. Se hai altre informazioni, come la lunghezza di un lato e un angolo, dovrai utilizzare metodi diversi per calcolare l'area. * Pratica con diversi esempi per familiarizzare con la formula e applicarla correttamente.

Speriamo che questo articolo ti abbia fornito una comprensione chiara e completa di come calcolare l'area di un rombo utilizzando le sue diagonali. Ora sei equipaggiato per affrontare problemi geometrici che coinvolgono questa affascinante figura! Metti in pratica le tue nuove conoscenze e non esitare a esplorare altre proprietà e applicazioni del rombo.