Come Si Calcola L'altezza Di Una Piramide

Capire come calcolare l'altezza di una piramide è un concetto fondamentale in geometria. Sebbene possa sembrare complesso a prima vista, la formula e il procedimento sono abbastanza accessibili una volta compresi i principi base. Questo articolo mira a fornire una guida chiara e dettagliata su come affrontare questo calcolo, esplorando diversi scenari e fornendo esempi pratici.

Comprendere la Geometria di Base della Piramide

Prima di immergerci nei calcoli, è cruciale avere una solida comprensione della geometria di una piramide. Una piramide è un solido geometrico formato collegando una base poligonale a un punto, detto apice. La base può essere un triangolo, un quadrato, un pentagono o qualsiasi altro poligono. L'altezza della piramide è la distanza perpendicolare dall'apice al centro della base. È importante non confondere l'altezza della piramide con l'apotema, che è l'altezza di una delle facce triangolari laterali.

Definizioni Chiave

Per poter calcolare l'altezza di una piramide, è essenziale definire alcuni termini chiave:

Base (B): Il poligono che forma la base della piramide.
Area della Base (Ab): L'area della superficie del poligono di base. Il calcolo di questa area varia a seconda della forma della base.
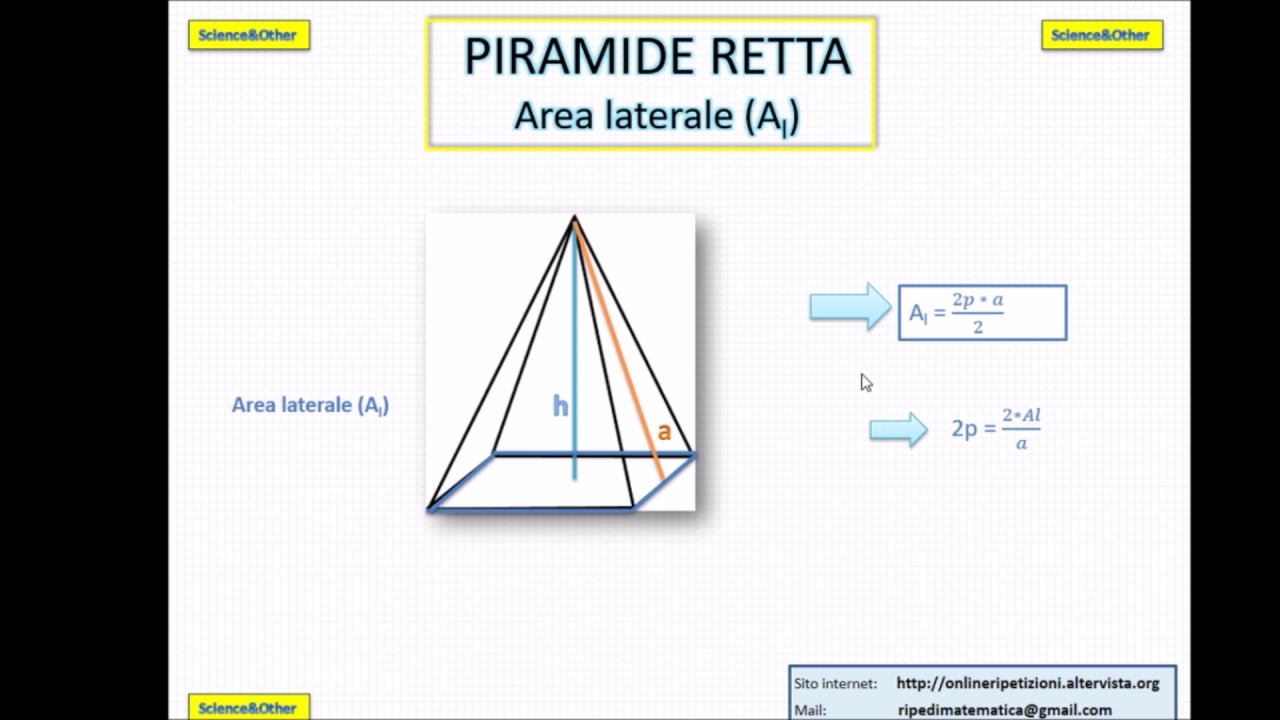
Apotema (a): L'altezza di una faccia laterale triangolare della piramide.
Altezza (h): La distanza perpendicolare dall'apice al centro della base. Questa è la grandezza che vogliamo calcolare.
Lato della Base (l): La lunghezza di un lato del poligono di base.
Volume (V): Lo spazio tridimensionale racchiuso dalla piramide.

Metodi per Calcolare l'Altezza di una Piramide

Esistono diversi metodi per calcolare l'altezza di una piramide, a seconda delle informazioni disponibili. I metodi più comuni includono l'utilizzo del volume, l'utilizzo dell'apotema e del lato della base (in particolare per piramidi a base quadrata o triangolare), e l'utilizzo del teorema di Pitagora.

Calcolo dell'Altezza Usando il Volume

Il metodo più diretto per calcolare l'altezza di una piramide è utilizzare la formula del volume. La formula per il volume di una piramide è:

V = (1/3) * Ab * h

Dove:

V è il volume della piramide
Ab è l'area della base
h è l'altezza della piramide

Se conosciamo il volume (V) e l'area della base (Ab), possiamo riorganizzare la formula per risolvere per l'altezza (h):

h = (3 * V) / Ab

Esempio: Supponiamo di avere una piramide con un volume di 150 cm³ e una base quadrata con un'area di 25 cm². L'altezza della piramide sarebbe:

h = (3 * 150) / 25 = 450 / 25 = 18 cm

Quindi, l'altezza della piramide è di 18 cm.

Calcolo dell'Altezza Usando l'Apotema e il Lato della Base (Piramidi a Base Quadrata)

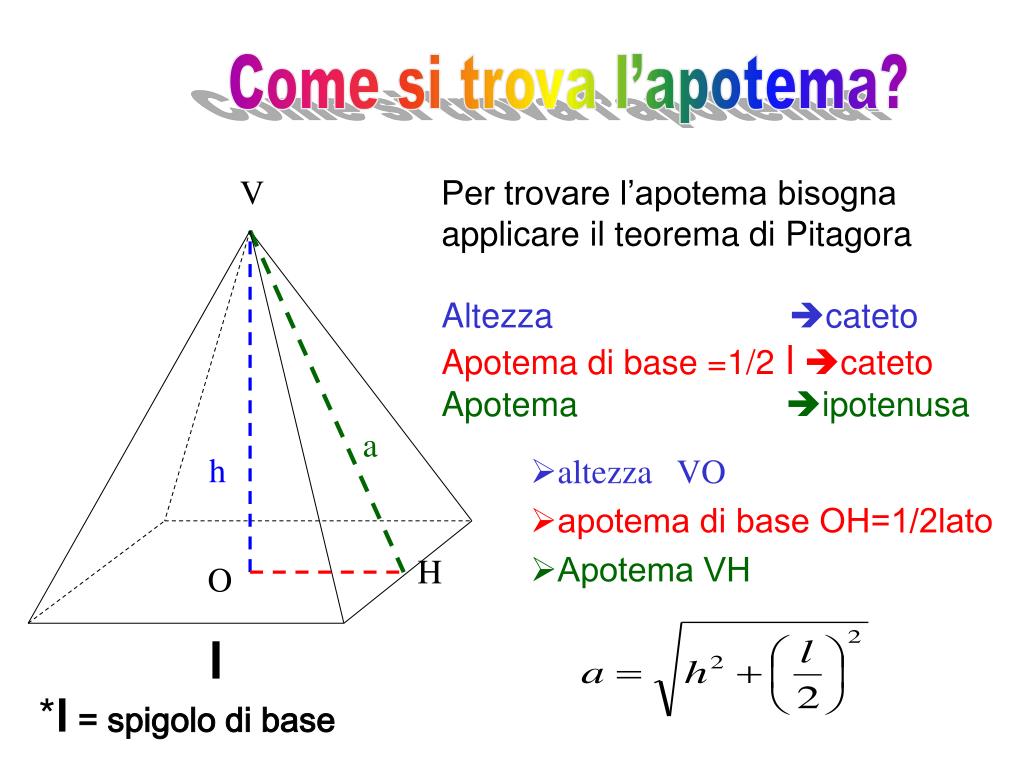
Questo metodo è specifico per le piramidi a base quadrata. Si basa sulla relazione tra l'apotema (a), il lato della base (l) e l'altezza (h) attraverso il teorema di Pitagora. Immaginiamo un triangolo rettangolo formato dall'altezza della piramide, metà del lato della base e l'apotema. L'apotema è l'ipotenusa di questo triangolo, mentre l'altezza e metà del lato della base sono i cateti. Pertanto, possiamo scrivere:

a² = h² + (l/2)²

Riorganizzando la formula per risolvere per l'altezza (h):

h = √(a² - (l/2)²)

Esempio: Consideriamo una piramide a base quadrata con un apotema di 13 cm e un lato della base di 10 cm. L'altezza della piramide sarebbe:

h = √(13² - (10/2)²) = √(169 - 25) = √144 = 12 cm

Quindi, l'altezza della piramide è di 12 cm.

Calcolo dell'Altezza Usando l'Apotema e il Lato della Base (Piramidi a Base Triangolare Equilatera)

Per le piramidi a base triangolare equilatera, il procedimento è simile, ma è necessario calcolare la distanza dal centro del triangolo equilatero al suo vertice. Questa distanza è pari a (l * √3)/3, dove l è il lato del triangolo. Quindi, l'altezza si calcola usando il teorema di Pitagora:

a² = h² + ((l * √3)/3)²

Riorganizzando la formula per risolvere per l'altezza (h):

h = √(a² - ((l * √3)/3)²)

Esempio: Consideriamo una piramide a base triangolare equilatera con un apotema di 8 cm e un lato della base di 6 cm. L'altezza della piramide sarebbe:

h = √(8² - ((6 * √3)/3)²) = √(64 - (2√3)²) = √(64 - 12) = √52 ≈ 7.21 cm

Quindi, l'altezza della piramide è di circa 7.21 cm.

Utilizzo del Teorema di Pitagora in Scenari Generali

Il teorema di Pitagora (a² + b² = c²) può essere utilizzato in vari scenari per calcolare l'altezza di una piramide, a condizione che si conoscano le lunghezze di due lati di un triangolo rettangolo che include l'altezza come uno dei lati. Questo metodo è particolarmente utile quando si conoscono le lunghezze di uno spigolo laterale della piramide e la distanza dal centro della base al vertice più vicino.

Esempio: Immaginiamo una piramide la cui base è un rettangolo. Conosciamo la lunghezza di uno spigolo laterale (s) e le dimensioni del rettangolo di base (lunghezza L e larghezza W). La distanza dal centro del rettangolo a uno dei vertici si calcola come la metà della diagonale del rettangolo, ovvero √((L/2)² + (W/2)²). Se conosciamo "s" e la distanza dal centro della base al vertice, possiamo usare il teorema di Pitagora per calcolare l'altezza:

s² = h² + ((L/2)² + (W/2)²)

h = √(s² - ((L/2)² + (W/2)²))

Esempi Reali e Dati

Il calcolo dell'altezza di una piramide non è solo un esercizio teorico. Ha applicazioni pratiche in architettura, ingegneria e archeologia. Ad esempio, gli ingegneri utilizzano questi calcoli per progettare strutture piramidali stabili e resistenti. Gli archeologi possono utilizzare le misurazioni di una piramide antica per stimarne il volume originale e quindi dedurre informazioni sulla sua costruzione e sul lavoro necessario per realizzarla.

Le piramidi egizie sono un esempio classico. La Grande Piramide di Giza, originariamente alta circa 146.6 metri, offre un esempio concreto di come i principi geometrici sono stati applicati in un progetto di costruzione monumentale. Calcolare l'altezza di questa piramide, date le sue dimensioni di base e l'angolo delle facce, è un esercizio interessante che dimostra la potenza dei concetti geometrici discussi.

Considerazioni Pratiche e Errori Comuni

Quando si calcola l'altezza di una piramide, è fondamentale prestare attenzione alle unità di misura. Assicurarsi che tutte le misure siano nella stessa unità (ad esempio, centimetri, metri, pollici) per evitare errori nei calcoli. Un errore comune è confondere l'altezza della piramide con l'apotema. È cruciale identificare correttamente quale lunghezza è fornita nel problema.

Un altro errore comune è l'uso errato della formula dell'area della base. Assicurarsi di utilizzare la formula corretta per calcolare l'area della base, a seconda della forma del poligono di base (quadrato, triangolo, pentagono, ecc.).

Conclusione

Calcolare l'altezza di una piramide è un'abilità fondamentale in geometria, con applicazioni pratiche in vari campi. Comprendendo i concetti base, le formule e i metodi discussi in questo articolo, sarai in grado di affrontare con sicurezza questo tipo di problema. Ricorda sempre di identificare le informazioni disponibili, scegliere il metodo appropriato e prestare attenzione alle unità di misura. Esercitati con diversi esempi per consolidare la tua comprensione e non aver paura di consultare risorse aggiuntive se necessario.