Come Si Calcola La Superficie Laterale Di Una Piramide

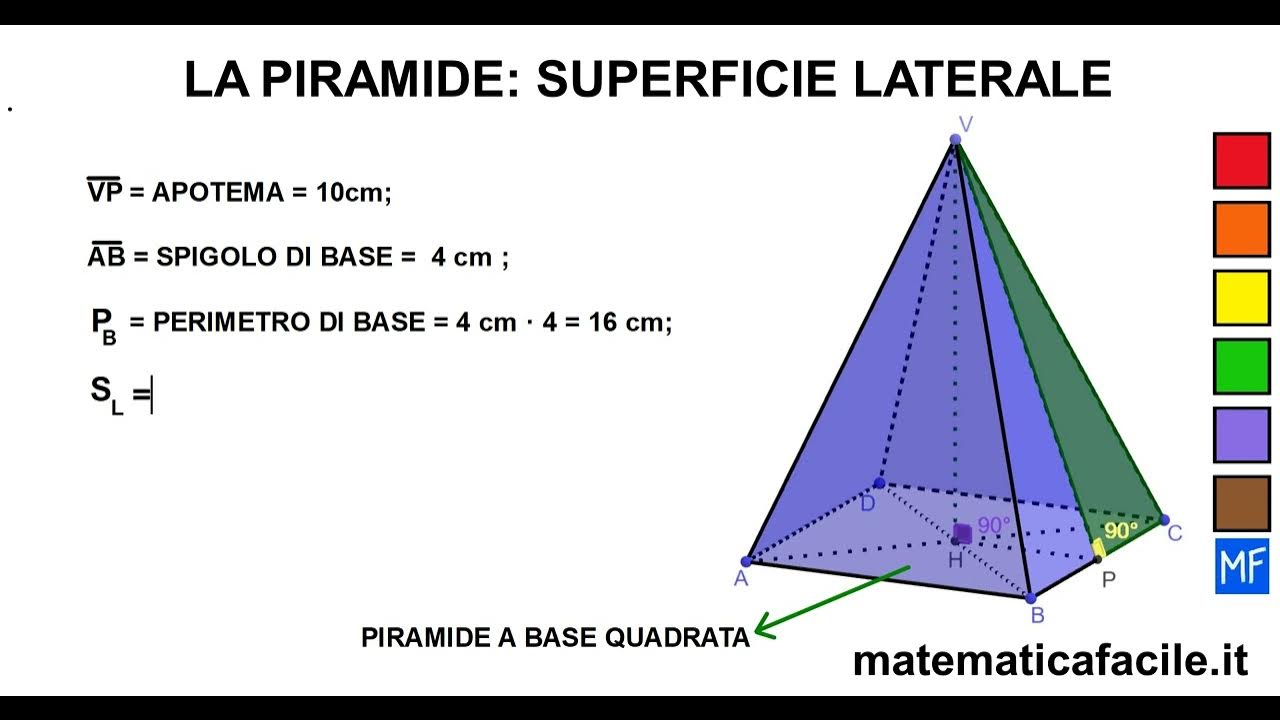
Calcolare la superficie laterale di una piramide è un concetto fondamentale nella geometria solida. Che tu stia studiando per un esame, progettando un tetto o semplicemente esplorando le forme geometriche, comprendere come si determina questa superficie è cruciale. Questo articolo ti guiderà attraverso il processo, fornendo una spiegazione dettagliata, esempi pratici e consigli utili.

Concetti Fondamentali: Di cosa abbiamo bisogno?

Prima di immergerci nei calcoli specifici, è essenziale avere una solida comprensione dei concetti di base. La superficie laterale di una piramide si riferisce alla somma delle aree di tutte le sue facce laterali, escludendo l'area della base.

Definizione di Piramide

Una piramide è un poliedro formato collegando un punto, chiamato apice o vertice, a tutti i vertici di un poligono (la base). Le facce laterali sono sempre triangoli.

Elementi Chiave

Per calcolare la superficie laterale, avrai bisogno di conoscere i seguenti elementi:

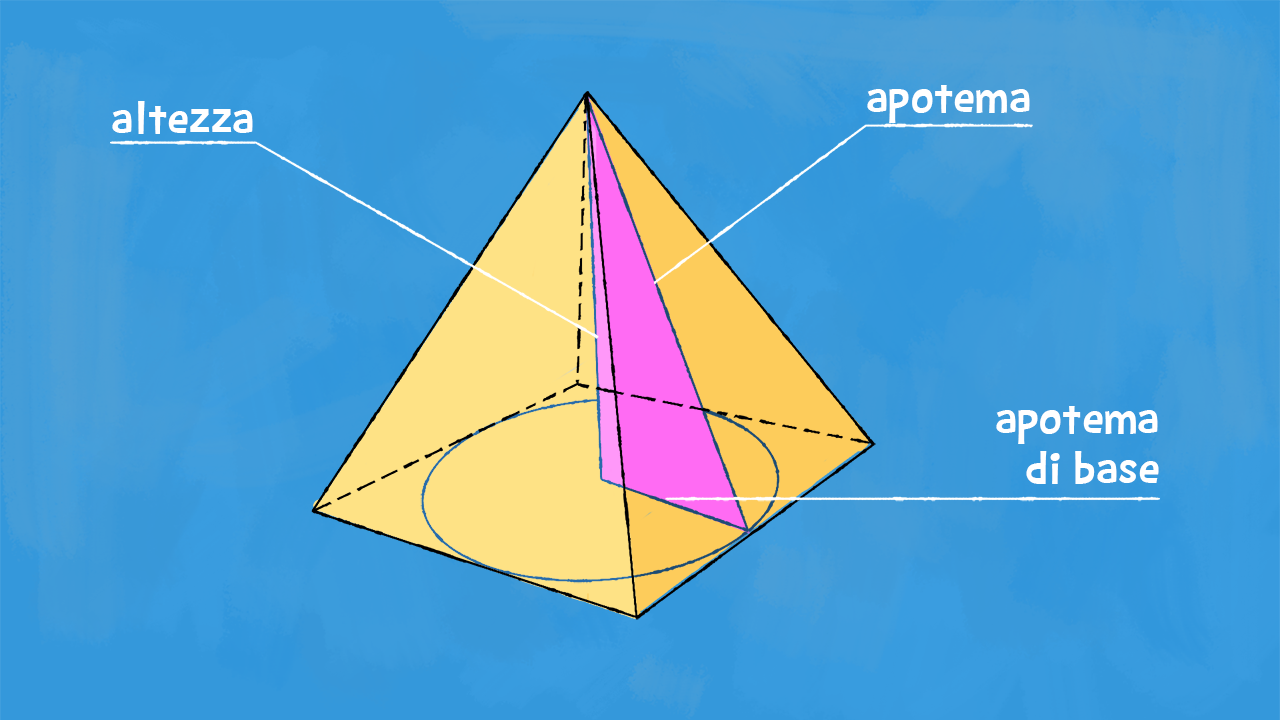
Apotema della piramide (a): L'altezza di una delle facce laterali, misurata dal vertice della piramide al punto medio di un lato della base.
Perimetro della base (P): La somma delle lunghezze di tutti i lati della base.
Area della base (Ab): L'area del poligono che forma la base della piramide. (Non necessaria per calcolare la superficie laterale, ma utile per trovare la superficie totale.)

La Formula Magica: Come si Calcola

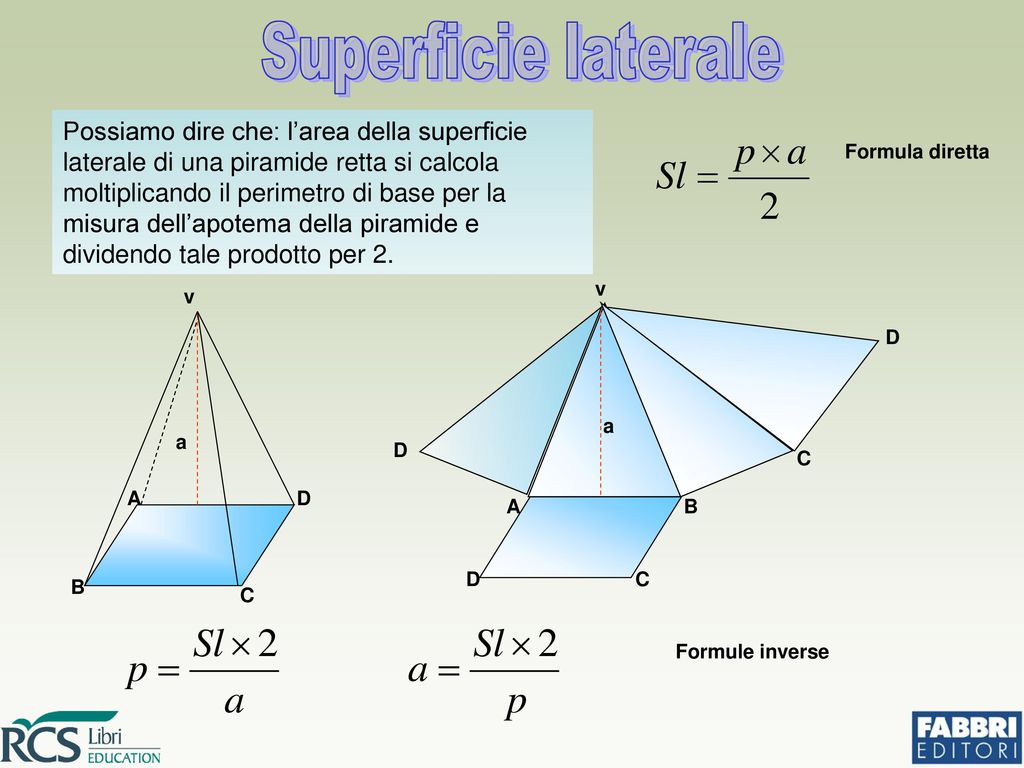
La formula generale per calcolare la superficie laterale (Sl) di una piramide è piuttosto semplice:

Sl = (P * a) / 2

Dove:

Sl = Superficie laterale
P = Perimetro della base
a = Apotema della piramide

Spiegazione Dettagliata della Formula

Questa formula deriva dal fatto che ogni faccia laterale è un triangolo. L'area di un triangolo è (base * altezza) / 2. In questo caso, la base del triangolo è un lato del poligono di base della piramide e l'altezza è l'apotema della piramide. Sommando le aree di tutti questi triangoli (che sono tutti uguali se la piramide è retta e la base è un poligono regolare), otteniamo la formula sopra.

Esempi Pratici: Mettiamoci al Lavoro

Per rendere il concetto ancora più chiaro, consideriamo alcuni esempi pratici.

Esempio 1: Piramide a Base Quadrata

Immagina una piramide con una base quadrata di lato 6 cm e un'apotema di 5 cm.

Calcola il perimetro della base (P): Poiché la base è un quadrato, P = 4 * lato = 4 * 6 cm = 24 cm.
Applica la formula: Sl = (P * a) / 2 = (24 cm * 5 cm) / 2 = 60 cm².

Quindi, la superficie laterale della piramide è di 60 cm².

Esempio 2: Piramide a Base Triangolare (Tetraedro Regolare)

Consideriamo un tetraedro regolare (una piramide con tutte le facce triangolari equilatere) con un lato di base di 4 cm e un'apotema di 3.5 cm.

Calcola il perimetro della base (P): Poiché la base è un triangolo equilatero, P = 3 * lato = 3 * 4 cm = 12 cm.
Applica la formula: Sl = (P * a) / 2 = (12 cm * 3.5 cm) / 2 = 21 cm².

Quindi, la superficie laterale del tetraedro regolare è di 21 cm².

Esempio 3: Piramide con Base Esagonale

Supponiamo di avere una piramide con una base esagonale regolare di lato 5 cm e un apotema di 8 cm.

Calcola il perimetro della base (P): Poiché la base è un esagono regolare, P = 6 * lato = 6 * 5 cm = 30 cm.
Applica la formula: Sl = (P * a) / 2 = (30 cm * 8 cm) / 2 = 120 cm².

La superficie laterale di questa piramide è 120 cm².

Piramide Obliqua: Una Sfida Aggiuntiva

Finora abbiamo considerato piramidi rette, in cui l'apice si trova direttamente sopra il centro della base. Ma cosa succede se la piramide è obliqua? In questo caso, le facce laterali non saranno tutte uguali e avranno apotemi diversi.

Per calcolare la superficie laterale di una piramide obliqua, è necessario calcolare l'area di ogni faccia laterale individualmente e poi sommare tutte le aree.

Sl (Piramide Obliqua) = Area Triangolo 1 + Area Triangolo 2 + Area Triangolo 3 + ...

Questo richiede di conoscere la lunghezza di ogni lato della base e l'apotema di ciascuna faccia laterale.

Applicazioni nel Mondo Reale: Dove Incontriamo le Piramidi

Le piramidi non sono solo figure geometriche astratte; si trovano in molte applicazioni del mondo reale:

Architettura: Le piramidi sono state utilizzate come strutture monumentali per secoli, dalle piramidi egizie alle piramidi Maya e Azteche. Le piramidi moderne possono essere trovate in edifici come la piramide del Louvre a Parigi.
Tetti: Alcuni tetti hanno una forma piramidale, soprattutto nelle strutture religiose o nei gazebo. Calcolare la superficie laterale è fondamentale per stimare i materiali necessari per la copertura.
Packaging: Alcune confezioni di prodotti alimentari o cosmetici possono avere una forma piramidale, offrendo un design accattivante e ottimizzando lo spazio.
Geometria Descrittiva e Grafica: La comprensione delle proprietà delle piramidi è essenziale per la rappresentazione grafica di oggetti tridimensionali.

Consigli Utili: Evitare Errori Comuni

Ecco alcuni consigli per evitare errori comuni nel calcolo della superficie laterale di una piramide:

Confondere l'apotema della piramide con l'apotema della base: Sono due concetti diversi. L'apotema della piramide è l'altezza di una faccia laterale, mentre l'apotema della base è la distanza dal centro della base al punto medio di un lato della base.
Dimenticare di dividere per 2: La formula per l'area di un triangolo è (base * altezza) / 2. Non dimenticare di dividere per 2 quando calcoli l'area di ciascuna faccia laterale.
Utilizzare unità di misura coerenti: Assicurati che tutte le misure (lato della base, apotema) siano espresse nella stessa unità di misura (ad esempio, centimetri o metri).
Considerare la piramide obliqua: Se la piramide è obliqua, non puoi usare la formula semplice Sl = (P * a) / 2. Devi calcolare l'area di ogni faccia laterale individualmente.

Conclusione: Padronanza della Superficie Laterale

Calcolare la superficie laterale di una piramide è una competenza essenziale nella geometria. Con una solida comprensione dei concetti di base, della formula e dei passaggi necessari, sarai in grado di risolvere facilmente una varietà di problemi. Ricorda di prestare attenzione alle diverse tipologie di piramidi (rette e oblique) e di utilizzare unità di misura coerenti. Con la pratica, diventerai un maestro nel calcolo della superficie laterale delle piramidi.

Ora che hai appreso i fondamenti, prova a risolvere alcuni esercizi. Sfida te stesso con piramidi di diverse forme e dimensioni. Più ti eserciti, più diventerai sicuro delle tue capacità. Buona fortuna!