Come Si Calcola La Diagonale Del Quadrato

Capita a tutti, prima o poi, di trovarsi di fronte a un quadrato e di aver bisogno di calcolarne la diagonale. Magari stai ristrutturando casa, progettando un mobile, o semplicemente aiutando tuo figlio con i compiti di geometria. La buona notizia è che calcolare la diagonale di un quadrato è più semplice di quanto possa sembrare. Cercheremo di rendere questo processo il più chiaro e accessibile possibile.

In questo articolo, esploreremo il calcolo della diagonale di un quadrato, partendo dalle basi e arrivando a metodi più rapidi e intuitivi. Niente formule astruse o gergo tecnico incomprensibile. Solo spiegazioni semplici e dirette, pensate per chiunque.

Perché Dovresti Sapere Come Calcolare la Diagonale di un Quadrato?

Potresti pensare che calcolare la diagonale di un quadrato sia un'abilità puramente teorica, utile solo a scuola. In realtà, conoscere questo concetto può avere applicazioni pratiche nella vita di tutti i giorni. Ecco alcuni esempi:

• Progettazione e Costruzione: Se stai costruendo un mobile o ristrutturando una stanza, potresti aver bisogno di calcolare la diagonale per assicurarti che gli angoli siano retti e che gli elementi siano allineati correttamente. Immagina di dover tagliare un pezzo di legno a forma di triangolo rettangolo per rinforzare l'angolo di un mobile; la diagonale del quadrato ti aiuterebbe a determinare la lunghezza dell'ipotenusa.
• Giardinaggio e Paesaggistica: Quando progetti un giardino, potresti voler creare aiuole quadrate o posizionare elementi decorativi in modo simmetrico. Calcolare la diagonale ti aiuta a determinare le distanze corrette e a garantire un aspetto armonioso.
• Design Grafico e Arte: Anche nel mondo dell'arte e del design, la geometria gioca un ruolo importante. Conoscere le proprietà dei quadrati e delle loro diagonali può aiutarti a creare composizioni equilibrate e visivamente accattivanti.
• Navigazione e Orientamento: Se stai usando una mappa o un sistema di navigazione, potresti aver bisogno di calcolare la distanza in linea d'aria tra due punti. In alcuni casi, questa distanza può essere approssimata con la diagonale di un quadrato.

Questi sono solo alcuni esempi, ma dimostrano come la geometria, e in particolare la conoscenza del quadrato e della sua diagonale, possa essere utile in una varietà di contesti.

Le Basi: Cos'è un Quadrato e Cos'è una Diagonale?

Prima di addentrarci nel calcolo, ripassiamo brevemente le definizioni di quadrato e diagonale:

• Quadrato: Un quadrato è un quadrilatero (una figura geometrica con quattro lati) che ha tutti e quattro i lati uguali e tutti e quattro gli angoli retti (angoli di 90 gradi).
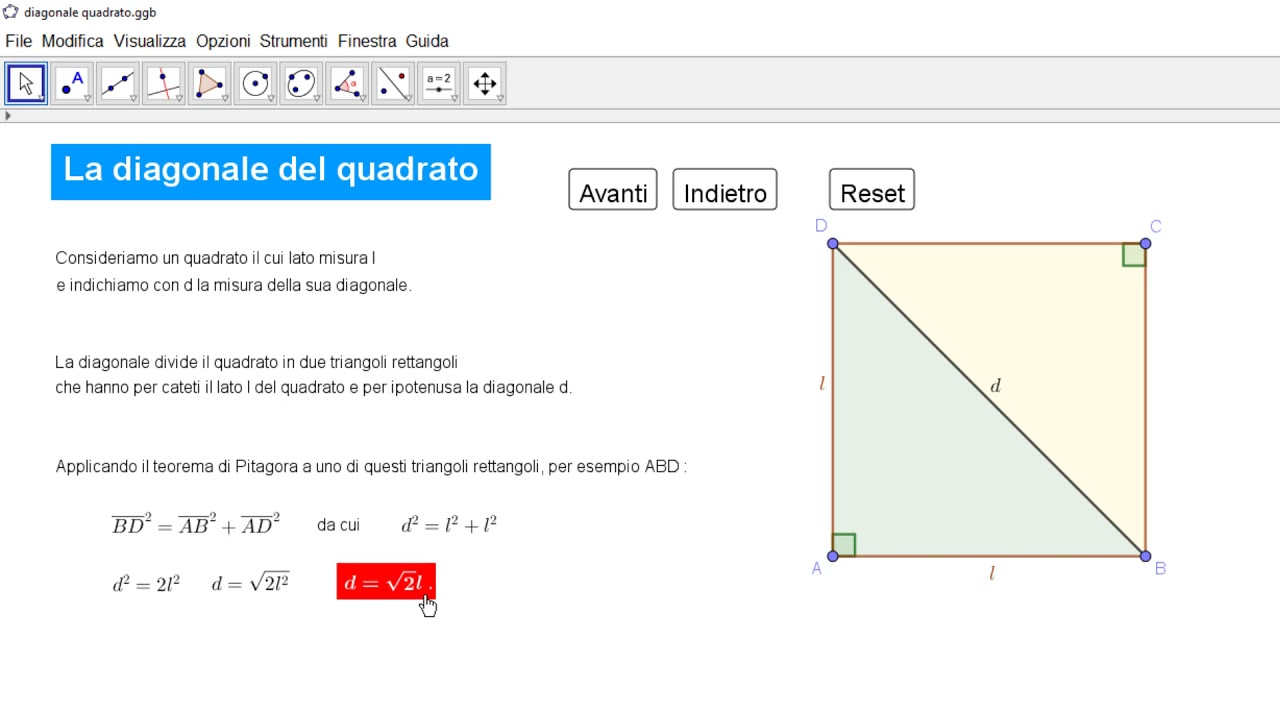
• Diagonale: Una diagonale è un segmento di retta che congiunge due vertici non consecutivi di un poligono. In un quadrato, ci sono due diagonali, entrambe di uguale lunghezza.

La diagonale di un quadrato lo divide in due triangoli rettangoli isosceli. Questo è un concetto chiave che ci aiuterà a capire come calcolarla.

Il Teorema di Pitagora: La Chiave per Calcolare la Diagonale

Il Teorema di Pitagora è un pilastro della geometria e ci fornisce lo strumento fondamentale per calcolare la diagonale del quadrato. Il teorema afferma che in un triangolo rettangolo, il quadrato dell'ipotenusa (il lato opposto all'angolo retto) è uguale alla somma dei quadrati degli altri due lati (i cateti). In formula:

a² + b² = c²

Dove:

• a e b sono le lunghezze dei cateti
• c è la lunghezza dell'ipotenusa

Nel caso del quadrato, come abbiamo detto, la diagonale lo divide in due triangoli rettangoli isosceli. I lati del quadrato diventano i cateti del triangolo rettangolo, e la diagonale diventa l'ipotenusa. Quindi, possiamo riscrivere il Teorema di Pitagora in questo modo:

lato² + lato² = diagonale²

Dove "lato" è la lunghezza di un lato del quadrato e "diagonale" è la lunghezza della diagonale.

Calcoliamo la Diagonale Passo Dopo Passo

Ora che abbiamo il Teorema di Pitagora, possiamo calcolare la diagonale del quadrato. Ecco i passaggi:

1. Conosci la lunghezza del lato: Questo è il primo passo fondamentale. Devi sapere quanto misura un lato del quadrato.
2. Applica il Teorema di Pitagora: Usa la formula: lato² + lato² = diagonale²
3. Semplifica l'equazione: Poiché lato² + lato² = 2 * lato², possiamo scrivere: 2 * lato² = diagonale²
4. Estrai la radice quadrata: Per trovare la diagonale, devi estrarre la radice quadrata di entrambi i lati dell'equazione: √(2 * lato²) = √(diagonale²)
5. Semplifica la radice: La radice quadrata di diagonale² è semplicemente diagonale. La radice quadrata di 2 * lato² può essere semplificata come lato * √2.

Quindi, la formula finale per calcolare la diagonale di un quadrato è:

diagonale = lato * √2

Dove √2 (radice quadrata di 2) è approssimativamente uguale a 1.4142.

Esempio Pratico

Supponiamo di avere un quadrato con un lato di 5 cm. Quanto misura la sua diagonale?

Usiamo la formula:

diagonale = lato * √2

diagonale = 5 cm * 1.4142

diagonale ≈ 7.07 cm

Quindi, la diagonale del quadrato misura circa 7.07 cm.

Un Metodo Più Rapido: La Scorciatoia di √2

Come abbiamo visto, la formula per calcolare la diagonale di un quadrato è diagonale = lato * √2. Questo significa che la diagonale di un quadrato è sempre √2 volte la lunghezza del suo lato. Conoscere questo rapporto costante ti permette di calcolare la diagonale in modo molto più rapido.

Invece di applicare il Teorema di Pitagora ogni volta, puoi semplicemente moltiplicare la lunghezza del lato per √2 (o la sua approssimazione 1.4142). Questo metodo è particolarmente utile quando devi calcolare la diagonale di molti quadrati diversi.

Esempio Comparativo

Proviamo a calcolare la diagonale di un quadrato con lato di 10 cm usando entrambi i metodi:

Metodo 1: Teorema di Pitagora

lato² + lato² = diagonale²

10² + 10² = diagonale²

100 + 100 = diagonale²

200 = diagonale²

diagonale = √200 ≈ 14.14 cm

Metodo 2: Scorciatoia di √2

diagonale = lato * √2

diagonale = 10 cm * 1.4142

diagonale ≈ 14.14 cm

Come puoi vedere, entrambi i metodi portano allo stesso risultato, ma la scorciatoia di √2 è decisamente più veloce.

Cosa Fare Se Conosci la Diagonale e Vuoi Trovare il Lato?

A volte, potresti trovarti nella situazione opposta: conosci la lunghezza della diagonale di un quadrato e vuoi calcolare la lunghezza del suo lato. In questo caso, possiamo semplicemente ricavare il lato dalla formula che abbiamo già:

diagonale = lato * √2

Dividendo entrambi i lati dell'equazione per √2, otteniamo:

lato = diagonale / √2

Quindi, per trovare il lato di un quadrato conoscendo la diagonale, devi dividere la lunghezza della diagonale per √2 (o la sua approssimazione 1.4142).

Esempio:

Supponiamo di avere un quadrato con una diagonale di 8 cm. Quanto misura il suo lato?

Usiamo la formula:

lato = diagonale / √2

lato = 8 cm / 1.4142

lato ≈ 5.66 cm

Quindi, il lato del quadrato misura circa 5.66 cm.

Errori Comuni da Evitare

Anche se il calcolo della diagonale di un quadrato è relativamente semplice, ci sono alcuni errori comuni che è bene evitare:

• Confondere il lato con la diagonale: Assicurati di utilizzare la lunghezza del lato del quadrato nella formula, e non la lunghezza della diagonale.
• Dimenticare il Teorema di Pitagora: Se non ricordi la formula diretta, puoi sempre ricorrere al Teorema di Pitagora.
• Arrotondare troppo presto: Se stai usando un'approssimazione di √2, cerca di arrotondare il risultato finale solo alla fine del calcolo, per evitare errori di approssimazione.
• Usare unità di misura diverse: Assicurati che tutte le lunghezze siano espresse nella stessa unità di misura (ad esempio, tutti in centimetri o tutti in metri).

Oltre la Formula: Comprendere il Concetto

Anche se imparare la formula diagonale = lato * √2 è utile, è ancora più importante capire il concetto che sta alla base. Comprendere il Teorema di Pitagora e il rapporto tra il lato e la diagonale di un quadrato ti permetterà di risolvere problemi più complessi e di applicare questi concetti in contesti diversi.

La geometria non è solo un insieme di formule da memorizzare, ma un modo di pensare e di risolvere problemi. Cerca di visualizzare le figure geometriche e di capire le loro proprietà. Questo ti aiuterà a sviluppare un intuito geometrico che ti sarà utile in molte situazioni.

Conclusione

Calcolare la diagonale di un quadrato è un'abilità utile e accessibile a tutti. Abbiamo visto come utilizzare il Teorema di Pitagora per derivare la formula, e come sfruttare la scorciatoia di √2 per calcoli più rapidi. Ricorda che la chiave è capire il concetto che sta alla base, piuttosto che memorizzare semplicemente la formula.

Ora, prova a mettere in pratica quello che hai imparato. Prendi un oggetto quadrato che hai a portata di mano, misurane il lato e calcolane la diagonale. Oppure, immagina di dover progettare un giardino quadrato e di dover calcolare la lunghezza della sua diagonale per posizionare un elemento decorativo. Più ti eserciti, più diventerai sicuro e competente nel calcolo della diagonale del quadrato.

Qual è la prima applicazione pratica che ti viene in mente, ora che sai come calcolare la diagonale di un quadrato?