Come Si Calcola L Ipotenusa Di Un Triangolo Rettangolo

Ti sei mai trovato di fronte a un triangolo rettangolo e ti sei chiesto come calcolare quella linea obliqua, l'ipotenusa? Forse stavi aiutando tuo figlio con i compiti, oppure stavi cercando di capire le dimensioni di un tetto per un progetto di bricolage. Qualunque sia la ragione, non sei solo! Molte persone si sentono intimidite dalla matematica, ma calcolare l'ipotenusa di un triangolo rettangolo è più semplice di quanto pensi. In questa guida, ti sveleremo il segreto dietro questo calcolo, rendendolo accessibile e comprensibile a tutti.
Il Teorema di Pitagora: La Chiave per Calcolare l'Ipotenusa
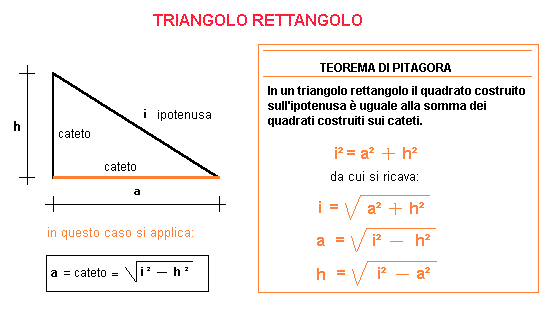
Il cuore di questo calcolo risiede nel Teorema di Pitagora, una delle pietre miliari della geometria. Questo teorema, attribuito al matematico greco Pitagora, stabilisce una relazione fondamentale tra i lati di un triangolo rettangolo. Ricorda, un triangolo rettangolo è un triangolo che ha un angolo di 90 gradi (un angolo retto).
La formula del Teorema di Pitagora è: a² + b² = c²
Dove:
- a e b sono le lunghezze dei cateti (i due lati che formano l'angolo retto).
- c è la lunghezza dell'ipotenusa (il lato opposto all'angolo retto, ed è il lato più lungo del triangolo rettangolo).
In parole semplici, il teorema dice che la somma dei quadrati dei cateti è uguale al quadrato dell'ipotenusa. Questo ci fornisce un metodo diretto per calcolare l'ipotenusa, conoscendo la lunghezza degli altri due lati.
Come Calcolare l'Ipotenusa: Passo dopo Passo
Ora che conosciamo il Teorema di Pitagora, vediamo come applicarlo concretamente per calcolare l'ipotenusa:
Passo 1: Identifica i Cateti
Innanzitutto, identifica chiaramente i cateti del tuo triangolo rettangolo. Ricorda, sono i due lati che formano l'angolo retto. Assicurati di conoscere le loro lunghezze.
Esempio: Supponiamo di avere un triangolo rettangolo con un cateto di lunghezza 3 cm (a = 3 cm) e un altro cateto di lunghezza 4 cm (b = 4 cm).
Passo 2: Calcola i Quadrati dei Cateti
Eleva al quadrato la lunghezza di ciascun cateto. Questo significa moltiplicare ogni lunghezza per se stessa.
Continuando con l'esempio:
- a² = 3 cm * 3 cm = 9 cm²
- b² = 4 cm * 4 cm = 16 cm²
Passo 3: Somma i Quadrati dei Cateti
Somma i risultati ottenuti nel passo precedente. Questa somma rappresenta il quadrato dell'ipotenusa (c²).
Ancora nel nostro esempio:
c² = 9 cm² + 16 cm² = 25 cm²
Passo 4: Calcola la Radice Quadrata
Per trovare la lunghezza dell'ipotenusa (c), devi calcolare la radice quadrata del risultato ottenuto al passo precedente. La radice quadrata di un numero è quel valore che, moltiplicato per se stesso, dà il numero originale.
Concludendo l'esempio:
c = √25 cm² = 5 cm
Pertanto, l'ipotenusa del triangolo rettangolo con cateti di 3 cm e 4 cm è di 5 cm.
Esempi Pratici per Comprendere Meglio
Per consolidare la tua comprensione, vediamo alcuni esempi aggiuntivi:
Esempio 1: Un triangolo rettangolo ha cateti di lunghezza 6 metri e 8 metri. Qual è la lunghezza dell'ipotenusa?
Soluzione:
- a = 6 m, b = 8 m
- a² = 36 m², b² = 64 m²
- c² = 36 m² + 64 m² = 100 m²
- c = √100 m² = 10 m
L'ipotenusa è lunga 10 metri.
Esempio 2: Un triangolo rettangolo ha un cateto di lunghezza 5 cm e un'ipotenusa di 13 cm. Qual è la lunghezza dell'altro cateto?
Soluzione: Qui dobbiamo manipolare leggermente la formula di Pitagora. Sappiamo che a² + b² = c², quindi b² = c² - a². Possiamo quindi ricavare b come la radice quadrata di (c² - a²).
- a = 5 cm, c = 13 cm
- a² = 25 cm², c² = 169 cm²
- b² = 169 cm² - 25 cm² = 144 cm²
- b = √144 cm² = 12 cm
L'altro cateto è lungo 12 cm.
Strumenti Utili per Calcolare l'Ipotenusa
Oggi, non è sempre necessario fare i calcoli a mano. Esistono numerosi strumenti online che possono semplificarti la vita:
- Calcolatrici scientifiche online: Molti siti web offrono calcolatrici scientifiche gratuite che possono calcolare radici quadrate e altri calcoli complessi.
- App per smartphone: Ci sono app dedicate al calcolo dell'ipotenusa, basta inserire i valori dei cateti e l'app farà il resto.
- Fogli di calcolo (Excel, Google Sheets): Puoi creare un semplice foglio di calcolo con la formula di Pitagora per automatizzare il calcolo.
Perché È Importante Sapere Come Calcolare l'Ipotenusa?
La capacità di calcolare l'ipotenusa di un triangolo rettangolo ha numerose applicazioni pratiche nella vita di tutti i giorni e in diversi campi professionali:
- Costruzioni: Gli architetti e gli ingegneri utilizzano il teorema di Pitagora per progettare edifici, ponti e altre strutture, assicurandosi che siano stabili e sicuri.
- Navigazione: I navigatori usano il teorema di Pitagora per calcolare distanze e rotte.
- Falegnameria e bricolage: Calcolare l'ipotenusa è essenziale per tagliare angoli precisi e costruire strutture dritte.
- Grafica e animazione: L'ipotenusa viene utilizzata per calcolare distanze e angoli in animazioni 2D e 3D.
- Sport: Calcolare distanze e traiettorie, ad esempio nel golf o nel biliardo.
Consigli Utili e Errori Comuni da Evitare
Ecco alcuni consigli per evitare errori comuni quando calcoli l'ipotenusa:
- Assicurati di lavorare con un triangolo rettangolo: Il teorema di Pitagora si applica solo ai triangoli rettangoli.
- Non confondere i cateti con l'ipotenusa: L'ipotenusa è sempre il lato opposto all'angolo retto ed è il lato più lungo.
- Utilizza le unità di misura corrette: Se i cateti sono misurati in centimetri, l'ipotenusa sarà misurata in centimetri.
- Non dimenticare di calcolare la radice quadrata: Dopo aver sommato i quadrati dei cateti, è fondamentale calcolare la radice quadrata per ottenere la lunghezza dell'ipotenusa.
- Controlla i tuoi calcoli: Rivedi i tuoi passaggi per assicurarti di non aver commesso errori di calcolo.
Calcolare l'ipotenusa di un triangolo rettangolo non deve essere un compito arduo. Con la comprensione del Teorema di Pitagora e la pratica, diventerai un esperto in men che non si dica. Ricorda, la matematica è uno strumento potente che può aiutarti a risolvere problemi in molti aspetti della tua vita. Non aver paura di affrontarla, e scoprirai che è più accessibile di quanto pensi!