Come Si Calcola L Altezza Del Rettangolo

Ti sei mai trovato davanti a un problema di geometria, bloccato nel tentativo di calcolare l'altezza di un rettangolo? Forse stai aiutando tuo figlio con i compiti, oppure ti serve per un progetto di bricolage, o magari sei semplicemente curioso di rispolverare le tue conoscenze matematiche. Qualunque sia il motivo, non preoccuparti: sei nel posto giusto! Calcolare l'altezza di un rettangolo è un'operazione piuttosto semplice, una volta compresi i concetti fondamentali. Questa guida ti accompagnerà passo dopo passo, con spiegazioni chiare, esempi pratici e consigli utili per affrontare qualsiasi situazione.

Comprendere i Fondamentali del Rettangolo

Prima di addentrarci nei calcoli, è importante avere ben chiari i concetti base. Un rettangolo è un quadrilatero (una figura geometrica con quattro lati) con le seguenti caratteristiche:

• Quattro angoli retti: Ogni angolo misura esattamente 90 gradi.
• Lati opposti uguali e paralleli: I lati che si trovano uno di fronte all'altro hanno la stessa lunghezza e non si incontrano mai.

I lati di un rettangolo vengono chiamati base (solitamente il lato orizzontale) e altezza (solitamente il lato verticale). L'area di un rettangolo rappresenta la superficie interna alla figura, mentre il perimetro è la somma delle lunghezze di tutti i suoi lati.

Ricorda: la base e l'altezza sono perpendicolari tra loro, ovvero formano un angolo retto.

Metodi per Calcolare l'Altezza del Rettangolo

Esistono diversi metodi per calcolare l'altezza di un rettangolo, a seconda delle informazioni che hai a disposizione. Vediamo i più comuni:

1. Conoscendo l'Area e la Base

Questo è il metodo più diretto e semplice. La formula per calcolare l'area di un rettangolo è:

Area = Base × Altezza

Se conosci l'area (A) e la base (b), puoi ricavare l'altezza (h) con la seguente formula:

Altezza = Area / Base

Esempio: Supponiamo di avere un rettangolo con un'area di 24 cm² e una base di 6 cm. Per trovare l'altezza, dividiamo l'area per la base: 24 cm² / 6 cm = 4 cm. Quindi, l'altezza del rettangolo è di 4 cm.

Consiglio: Assicurati di utilizzare le stesse unità di misura per l'area e la base. Se l'area è espressa in cm² e la base in metri, dovrai convertire una delle due misure prima di effettuare il calcolo.

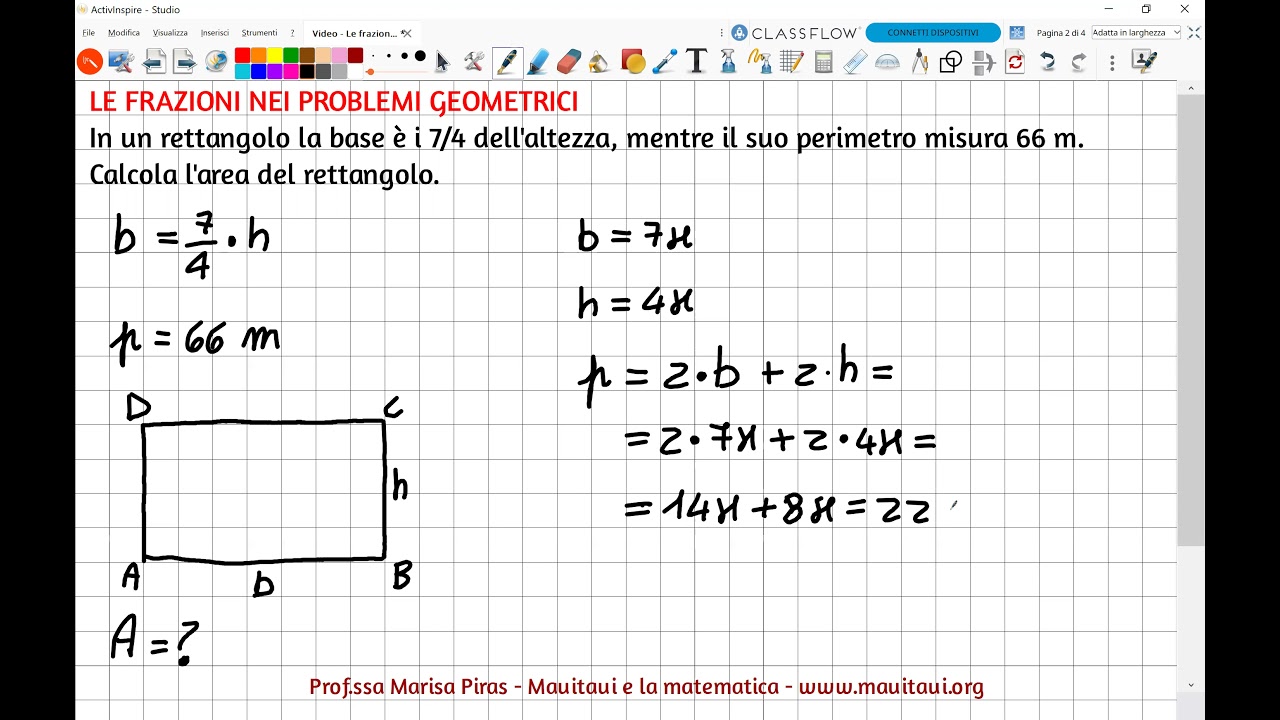
2. Conoscendo il Perimetro e la Base

Il perimetro di un rettangolo è la somma delle lunghezze di tutti i suoi lati. La formula per calcolarlo è:

Perimetro = 2 × (Base + Altezza)

Se conosci il perimetro (P) e la base (b), puoi ricavare l'altezza (h) con i seguenti passaggi:

1. Dividi il perimetro per 2: P / 2
2. Sottrai la base dal risultato ottenuto: (P / 2) - b

La formula finale è quindi:

Altezza = (Perimetro / 2) - Base

Esempio: Immaginiamo un rettangolo con un perimetro di 20 cm e una base di 7 cm. Per trovare l'altezza, seguiamo i passaggi:

• Dividiamo il perimetro per 2: 20 cm / 2 = 10 cm
• Sottraiamo la base dal risultato: 10 cm - 7 cm = 3 cm

Quindi, l'altezza del rettangolo è di 3 cm.

Attenzione: Ricorda che il perimetro è la somma di tutti i lati, quindi dividere per due serve a ottenere la somma di base e altezza.

3. Utilizzando il Teorema di Pitagora (Se conosci la Diagonale)

Se conosci la lunghezza della diagonale del rettangolo e la lunghezza della base, puoi utilizzare il teorema di Pitagora per calcolare l'altezza. La diagonale di un rettangolo divide quest'ultimo in due triangoli rettangoli. Il teorema di Pitagora afferma che in un triangolo rettangolo, il quadrato dell'ipotenusa (il lato opposto all'angolo retto) è uguale alla somma dei quadrati degli altri due lati (i cateti).

Nel nostro caso:

• La diagonale è l'ipotenusa.
• La base e l'altezza sono i cateti.

La formula del teorema di Pitagora è:

Diagonale² = Base² + Altezza²

Per ricavare l'altezza (h), dobbiamo riordinare la formula:

Altezza² = Diagonale² - Base²

Infine, estraiamo la radice quadrata di entrambi i lati per ottenere l'altezza:

Altezza = √(Diagonale² - Base²)

Esempio: Supponiamo di avere un rettangolo con una diagonale di 5 cm e una base di 4 cm. Per trovare l'altezza, seguiamo i passaggi:

• Eleviamo al quadrato la diagonale: 5 cm² = 25 cm²
• Eleviamo al quadrato la base: 4 cm² = 16 cm²
• Sottraiamo il quadrato della base dal quadrato della diagonale: 25 cm² - 16 cm² = 9 cm²
• Estraiamo la radice quadrata del risultato: √9 cm² = 3 cm

Quindi, l'altezza del rettangolo è di 3 cm.

Importante: Assicurati di utilizzare la calcolatrice per estrarre la radice quadrata, se necessario.

Consigli e Trucchi Utili

• Controlla sempre le unità di misura: Prima di effettuare qualsiasi calcolo, assicurati che tutte le misure siano espresse nella stessa unità.
• Disegna il rettangolo: Se hai difficoltà a visualizzare il problema, disegna un rettangolo e annota le informazioni che conosci. Questo ti aiuterà a capire meglio la situazione.
• Utilizza la calcolatrice: Non esitare a utilizzare una calcolatrice per semplificare i calcoli, soprattutto quando si tratta di estrarre radici quadrate o lavorare con numeri decimali.
• Verifica il risultato: Dopo aver calcolato l'altezza, verifica se il risultato è ragionevole. Ad esempio, l'altezza non può essere negativa o maggiore della diagonale.
• Esercitati: La pratica rende perfetti! Più ti eserciti a risolvere problemi di geometria, più diventerai bravo a calcolare l'altezza di un rettangolo (e non solo!).

Curiosità: Il rettangolo aureo, le cui dimensioni rispettano il rapporto aureo (circa 1.618), è considerato particolarmente armonioso e piacevole alla vista. È presente in molte opere d'arte e architettoniche.

In Conclusione

Calcolare l'altezza di un rettangolo non è affatto difficile, basta conoscere le formule giuste e applicarle correttamente. Con questa guida, hai imparato i metodi più comuni e hai ricevuto consigli utili per affrontare qualsiasi problema ti si presenti. Ora, armati di righello, calcolatrice e un po' di pazienza, e mettiti alla prova! Ricorda che la geometria, come qualsiasi altra disciplina, richiede pratica e dedizione. Ma con un po' di impegno, sarai in grado di risolvere qualsiasi sfida matematica!

Speriamo che questa guida ti sia stata utile. Se hai domande o dubbi, non esitare a chiedere! La matematica può essere divertente e gratificante, e siamo qui per aiutarti a scoprirlo.