Come Si Calcola Il Perimetro Di Un Triangolo Isoscele

Avete mai ammirato la perfetta simmetria di un triangolo isoscele? La sua forma elegante, con due lati uguali, si ritrova in natura, nell'architettura e persino nell'arte. Ma al di là della sua bellezza, la matematica ci offre gli strumenti per comprenderlo appieno, a partire dal calcolo del suo perimetro. Questa guida è pensata per tutti coloro che desiderano imparare a calcolare il perimetro di un triangolo isoscele: studenti, appassionati di geometria o semplicemente chi è curioso di scoprire i segreti di questa affascinante figura.
Cos'è un Triangolo Isoscele? Un Ripasso Fondamentale
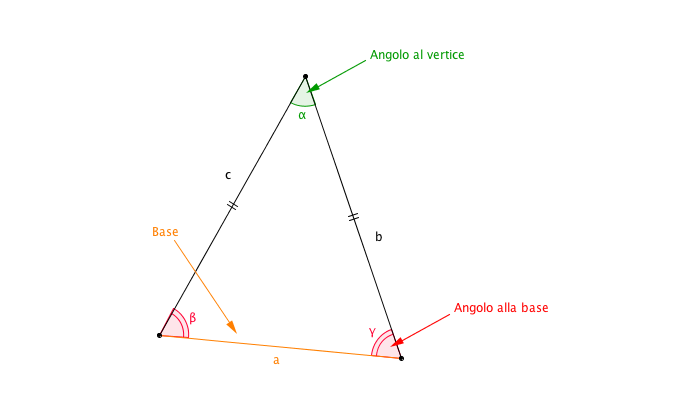
Prima di addentrarci nel calcolo del perimetro, è fondamentale definire cosa intendiamo per triangolo isoscele. Un triangolo isoscele è un triangolo che ha due lati di uguale lunghezza. Questi due lati uguali sono chiamati lati obliqui, mentre il terzo lato è detto base. Gli angoli opposti ai lati obliqui (gli angoli alla base) sono anch'essi uguali. Questa caratteristica di simmetria semplifica notevolmente i calcoli geometrici.
Differenza tra Triangolo Isoscele, Equilatero e Scaleno
È importante distinguere il triangolo isoscele da altri tipi di triangoli:
- Triangolo Equilatero: Ha tutti e tre i lati uguali e tutti gli angoli di 60 gradi. Di fatto, un triangolo equilatero è un caso speciale di triangolo isoscele.
- Triangolo Scaleno: Ha tutti e tre i lati di lunghezza diversa e tutti gli angoli diversi.
Calcolare il Perimetro: La Formula Base
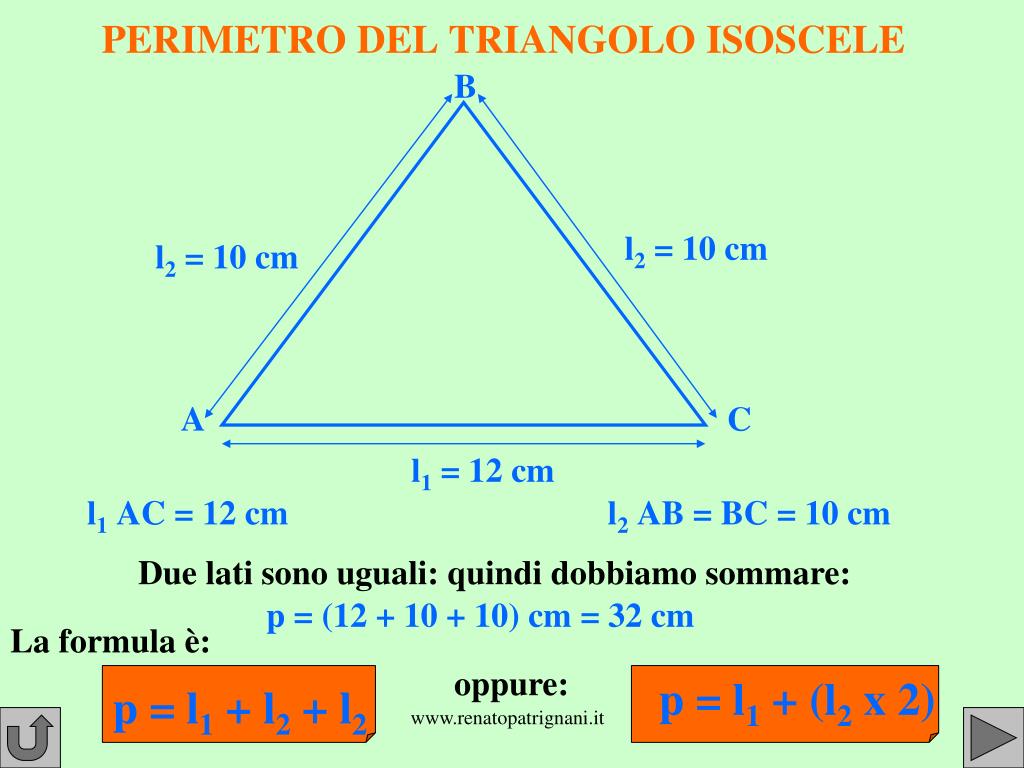
Il perimetro di qualsiasi poligono è semplicemente la somma della lunghezza di tutti i suoi lati. Nel caso di un triangolo isoscele, possiamo esprimerlo in modo più specifico. Sia l la lunghezza dei lati obliqui e b la lunghezza della base, allora la formula per calcolare il perimetro (P) è:
P = l + l + b oppure, più semplicemente, P = 2l + b
Questa formula è il punto di partenza per tutti i nostri calcoli. È essenziale memorizzarla e comprenderla a fondo.
Esempi Pratici per Comprendere Meglio
Per rendere il concetto più chiaro, vediamo alcuni esempi concreti:
Esempio 1: Conoscendo i Lati Obliqui e la Base
Supponiamo di avere un triangolo isoscele con lati obliqui di 8 cm ciascuno e una base di 5 cm. Applichiamo la formula:
P = (2 * 8 cm) + 5 cm = 16 cm + 5 cm = 21 cm
Il perimetro del triangolo è quindi di 21 cm.
Esempio 2: Conoscendo il Lato Obliquo e il Perimetro
Questa volta, immaginiamo di conoscere la lunghezza di un lato obliquo (l = 12 cm) e il perimetro (P = 35 cm). Dobbiamo trovare la lunghezza della base (b). Partiamo dalla formula:
P = 2l + b
Sostituiamo i valori noti:
35 cm = (2 * 12 cm) + b
35 cm = 24 cm + b
Ora isoliamo b:
b = 35 cm - 24 cm = 11 cm
La base del triangolo isoscele è di 11 cm.
Esempio 3: Applicazione nel Mondo Reale
Immaginate di dover costruire una cornice triangolare isoscele per una foto. Volete che i lati obliqui siano lunghi 20 cm e la base 15 cm. Quanto materiale vi serve in totale?
P = (2 * 20 cm) + 15 cm = 40 cm + 15 cm = 55 cm
Avrete bisogno di 55 cm di materiale per la cornice.
Quando le Cose si Complicano: Altezza e Teorema di Pitagora
In alcuni casi, potremmo non conoscere direttamente la lunghezza dei lati, ma avere informazioni sull'altezza del triangolo (la distanza perpendicolare dalla base al vertice opposto) e su una parte della base. In questi casi, possiamo utilizzare il Teorema di Pitagora per trovare la lunghezza dei lati obliqui.
Il Teorema di Pitagora
Il Teorema di Pitagora afferma che in un triangolo rettangolo (un triangolo con un angolo di 90 gradi), il quadrato dell'ipotenusa (il lato opposto all'angolo retto) è uguale alla somma dei quadrati degli altri due lati (i cateti). Matematicamente:
a2 + b2 = c2
Dove c è l'ipotenusa e a e b sono i cateti.
Applicare Pitagora al Triangolo Isoscele
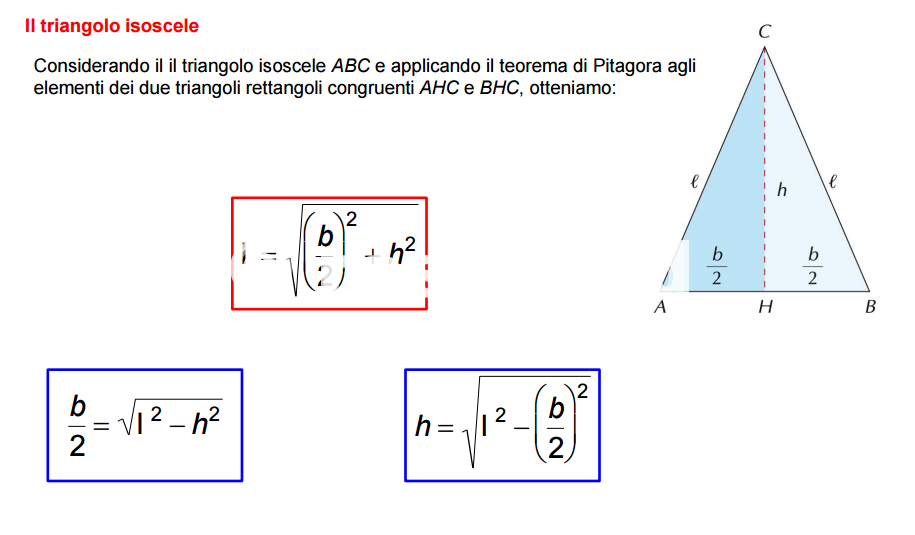
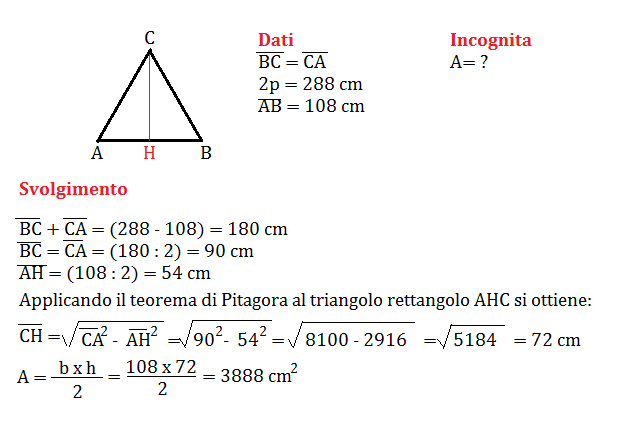
L'altezza di un triangolo isoscele divide la base a metà. Questo crea due triangoli rettangoli identici. L'altezza diventa uno dei cateti, metà della base diventa l'altro cateto, e il lato obliquo del triangolo isoscele diventa l'ipotenusa.
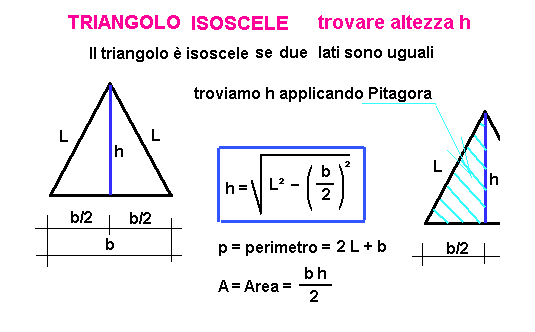
Se conosciamo l'altezza (h) e la metà della base (b/2), possiamo trovare il lato obliquo (l) usando il Teorema di Pitagora:
(b/2)2 + h2 = l2
Da qui, possiamo ricavare l: l = √( (b/2)2 + h2 )
Una volta trovato l, possiamo calcolare il perimetro come al solito: P = 2l + b.
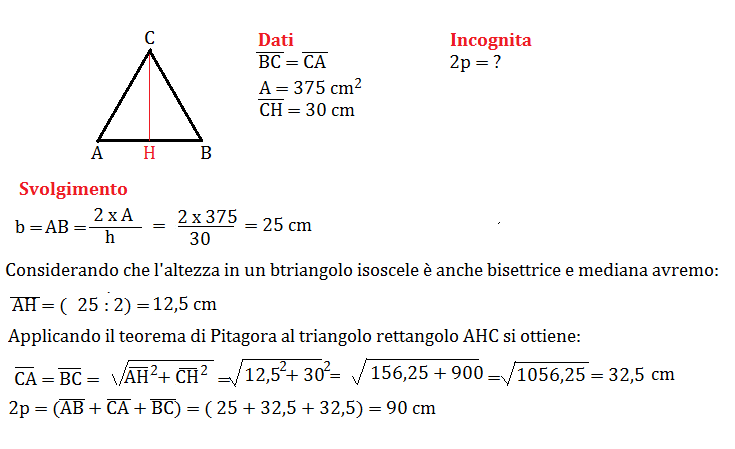
Esempio: Usando l'Altezza e la Base
Supponiamo di avere un triangolo isoscele con una base di 10 cm e un'altezza di 12 cm. Calcoliamo il lato obliquo:
l = √( (10 cm / 2)2 + (12 cm)2 ) = √( (5 cm)2 + (12 cm)2 ) = √( 25 cm2 + 144 cm2 ) = √169 cm2 = 13 cm
Ora possiamo calcolare il perimetro:
P = (2 * 13 cm) + 10 cm = 26 cm + 10 cm = 36 cm
Il perimetro del triangolo è di 36 cm.
Errori Comuni da Evitare
Durante il calcolo del perimetro di un triangolo isoscele, è importante evitare alcuni errori comuni:
- Confondere il triangolo isoscele con altri tipi di triangoli. Assicuratevi sempre di identificare correttamente i lati uguali e la base.
- Dimenticare di moltiplicare il lato obliquo per 2. La formula è P = 2l + b, non P = l + b.
- Fare errori di calcolo. Controllate sempre i vostri calcoli, soprattutto quando utilizzate il Teorema di Pitagora.
- Non utilizzare le unità di misura corrette. Assicuratevi che tutte le misure siano nella stessa unità (es. cm, metri, pollici) e che il risultato finale abbia l'unità di misura corretta.
Conclusione: Un Triangolo, Molte Possibilità
Calcolare il perimetro di un triangolo isoscele è un'abilità fondamentale in geometria. Abbiamo visto come la formula base P = 2l + b ci permette di trovare facilmente il perimetro conoscendo i lati. Abbiamo anche esplorato come utilizzare il Teorema di Pitagora quando abbiamo informazioni sull'altezza e sulla base. Con la pratica e la comprensione dei concetti fondamentali, sarete in grado di affrontare qualsiasi problema relativo ai triangoli isosceli con sicurezza e precisione. La geometria, dopotutto, non è solo una serie di formule, ma un modo per comprendere e apprezzare il mondo che ci circonda, dalla struttura di un tetto alla forma di una vela. Speriamo che questa guida vi sia stata utile e vi abbia fornito gli strumenti necessari per esplorare ulteriormente le meraviglie della geometria!