Come Si Calcola Il Perimetro Di Un Trapezio Rettangolo

Ciao! Se sei qui, probabilmente ti stai chiedendo "Come diavolo si calcola il perimetro di un trapezio rettangolo?". Non preoccuparti, non sei solo. Molti studenti (e anche qualche adulto!) si trovano di fronte a questo piccolo enigma geometrico. Ma la buona notizia è che, una volta compresi i concetti fondamentali, diventa molto più semplice. Cercheremo di rendere questo argomento accessibile a tutti, anche a chi si sente intimorito dalla matematica.

Prima di addentrarci nei calcoli veri e propri, proviamo a capire perché questo argomento è importante. Non si tratta solo di superare un compito in classe. La geometria, e in particolare la capacità di calcolare perimetri e aree, si applica in moltissimi contesti reali. Immagina di dover recintare un terreno con una forma irregolare, che assomiglia proprio a un trapezio rettangolo. Oppure, pensa a un falegname che deve costruire un tavolo con determinate dimensioni. Capire come calcolare il perimetro ti permette di stimare i materiali necessari, evitare sprechi e assicurarti che il tuo progetto abbia successo.

Cos'è un Trapezio Rettangolo?

Partiamo dalle basi. Un trapezio è un quadrilatero (una figura geometrica con quattro lati) con almeno due lati paralleli. Questi lati paralleli sono chiamati basi (una base maggiore e una base minore). Un trapezio rettangolo, in particolare, è un trapezio che ha due angoli retti (angoli di 90 gradi). Questo significa che uno dei lati non paralleli è perpendicolare alle basi, formando appunto un angolo retto.

Immagina un triangolo rettangolo a cui è stata tagliata la punta. Quello che resta è un trapezio rettangolo! Avere ben chiara questa immagine mentale ti aiuterà a visualizzare le proprietà e a ricordare le formule.

Elementi Chiave di un Trapezio Rettangolo:

Base Maggiore (B): Il lato parallelo più lungo.
Base Minore (b): Il lato parallelo più corto.
Altezza (h): Il lato perpendicolare alle basi (e quindi forma un angolo retto). È la distanza tra le due basi.
Lato Obliquo (l): Il lato non parallelo che non è perpendicolare alle basi.

Come Calcolare il Perimetro

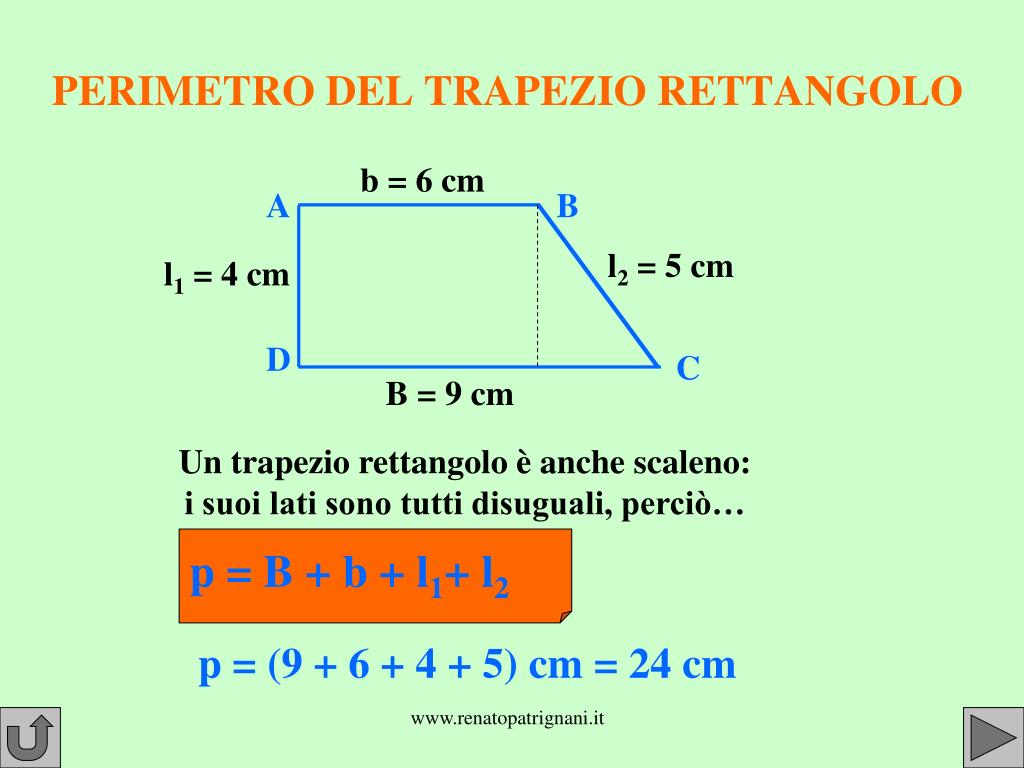
Il perimetro di qualsiasi figura geometrica è la somma della lunghezza di tutti i suoi lati. Quindi, per calcolare il perimetro di un trapezio rettangolo, dobbiamo sommare la lunghezza della base maggiore, della base minore, dell'altezza e del lato obliquo:

Perimetro (P) = B + b + h + l

Sembra semplice, vero? Il problema spesso è che non sempre conosciamo la lunghezza di tutti i lati. In particolare, la lunghezza del lato obliquo potrebbe non essere fornita direttamente.

Se Conosci Tutti i Lati:

Se il problema ti fornisce la lunghezza della base maggiore (B), della base minore (b), dell'altezza (h) e del lato obliquo (l), allora il calcolo del perimetro è estremamente semplice. Basta sommare questi valori.

Esempio: Se B = 10 cm, b = 6 cm, h = 4 cm, e l = 5 cm, allora P = 10 + 6 + 4 + 5 = 25 cm.

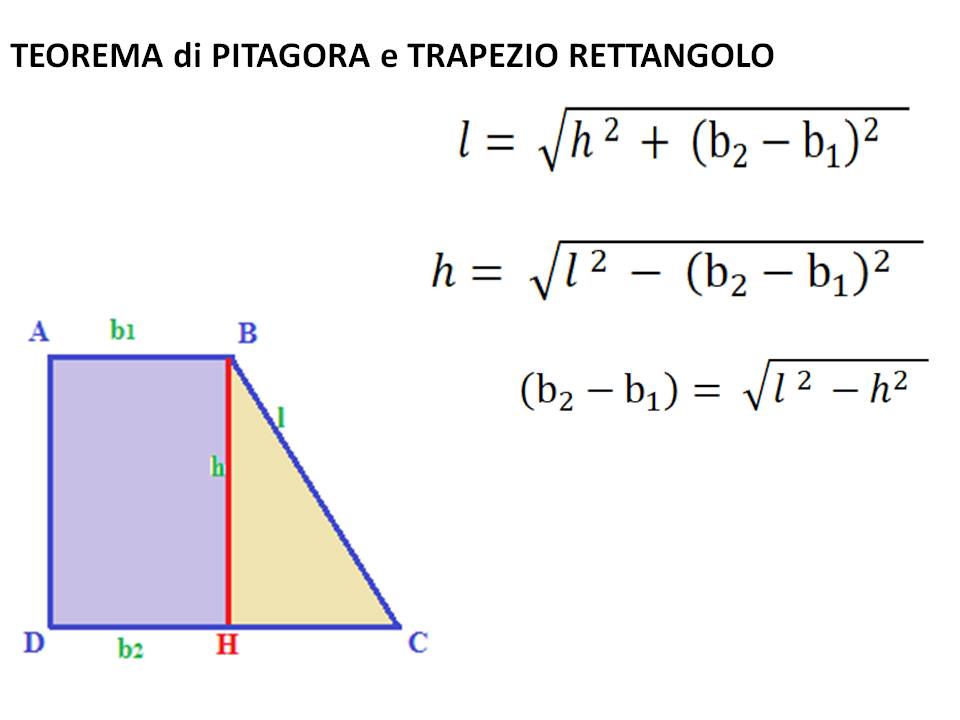
Se Non Conosci il Lato Obliquo: Teorema di Pitagora in Soccorso!

Qui entra in gioco il Teorema di Pitagora, un vero e proprio salvavita in geometria! Ricorda, il teorema di Pitagora afferma che in un triangolo rettangolo, il quadrato dell'ipotenusa (il lato opposto all'angolo retto) è uguale alla somma dei quadrati degli altri due lati (i cateti).

a² + b² = c²

Come possiamo applicare questo al nostro trapezio rettangolo? Immagina di tracciare una linea parallela all'altezza dal vertice della base minore fino alla base maggiore. Questa linea divide il trapezio rettangolo in un rettangolo e un triangolo rettangolo.

Il lato obliquo del trapezio rettangolo è l'ipotenusa del triangolo rettangolo che abbiamo creato. Uno dei cateti è l'altezza (h) del trapezio. L'altro cateto è la differenza tra la base maggiore (B) e la base minore (b): (B - b).

Ora possiamo applicare il Teorema di Pitagora per trovare il lato obliquo (l):

l² = h² + (B - b)²

Quindi, per trovare l, dobbiamo calcolare la radice quadrata di entrambi i lati dell'equazione:

l = √[h² + (B - b)²]

Una volta calcolato il lato obliquo (l), possiamo tornare alla formula originale per il perimetro: P = B + b + h + l.

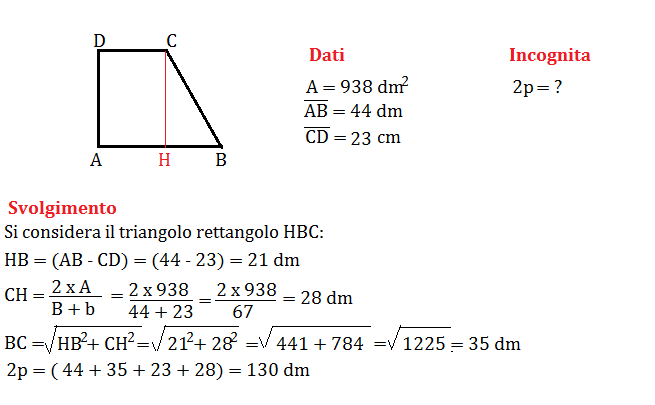
Esempio: Se B = 12 cm, b = 7 cm, e h = 5 cm, allora:

(B - b) = 12 - 7 = 5 cm
l² = 5² + 5² = 25 + 25 = 50
l = √50 ≈ 7.07 cm
P = 12 + 7 + 5 + 7.07 ≈ 31.07 cm

Un Approccio Alternativo

Alcuni preferiscono scomporre ulteriormente il problema. Invece di usare direttamente il Teorema di Pitagora, si può calcolare l'area del triangolo rettangolo e poi usare questa informazione (insieme all'altezza) per trovare il lato obliquo. Questo approccio è più lungo, ma può essere utile se hai difficoltà a visualizzare la relazione tra il triangolo e il trapezio.

Possibili Difficoltà e Come Superarle

Ecco alcune difficoltà comuni che gli studenti incontrano e come affrontarle:

Confondere i lati: Assicurati di identificare correttamente la base maggiore, la base minore, l'altezza e il lato obliquo. Disegna sempre un diagramma!
Dimenticare il Teorema di Pitagora: Il Teorema di Pitagora è fondamentale! Rivedilo se necessario. Ricorda che si applica solo ai triangoli rettangoli.
Errori di calcolo: Presta attenzione ai calcoli, soprattutto quando si elevano numeri al quadrato e si calcolano radici quadrate. Usa una calcolatrice se necessario.
Non capire la relazione tra le figure: Visualizza come il trapezio rettangolo può essere scomposto in un rettangolo e un triangolo rettangolo.

Controargomentazioni: Esistono Formule Più Complesse?

Potresti imbatterti in formule più complesse per il calcolo del perimetro del trapezio rettangolo. Queste formule spesso combinano direttamente il Teorema di Pitagora nella formula del perimetro, evitando un passaggio intermedio. Tuttavia, il metodo che abbiamo descritto è più intuitivo e ti permette di capire meglio da dove derivano i calcoli. Inoltre, ti aiuta a rafforzare la tua comprensione del Teorema di Pitagora, che è una competenza fondamentale in geometria.

Perché Dovresti Preoccuparti di Tutto Questo?

Come abbiamo detto all'inizio, la geometria non è solo teoria. Immagina di essere un architetto che progetta un edificio con finestre a forma di trapezio rettangolo. Oppure, pensa a un ingegnere che deve calcolare la quantità di materiale necessaria per costruire un ponte con una sezione trapezoidale. La capacità di calcolare il perimetro e l'area di queste figure è essenziale per il successo di questi progetti.

Anche in situazioni più quotidiane, questa conoscenza può essere utile. Ad esempio, potresti voler costruire un'aiuola nel tuo giardino con una forma particolare. Capire come calcolare il perimetro ti aiuterà a stimare la quantità di recinzione necessaria.

In Sintesi

Calcolare il perimetro di un trapezio rettangolo richiede di sommare la lunghezza di tutti i suoi lati. Se non conosci il lato obliquo, puoi usare il Teorema di Pitagora per calcolarlo, scomponendo il trapezio in un rettangolo e un triangolo rettangolo. Ricorda di disegnare un diagramma e di prestare attenzione ai calcoli. Con un po' di pratica, diventerai un esperto nel calcolo dei perimetri!

Spero che questa guida ti sia stata utile. Ora, prova a risolvere qualche esercizio da solo. La pratica è fondamentale per consolidare le tue conoscenze.

Sei pronto a mettere alla prova le tue nuove abilità? Cosa ne pensi di cercare online esercizi sul calcolo del perimetro di un trapezio rettangolo e provare a risolverli? Buon divertimento!