Come Si Calcola Il Perimetro Del Triangolo Rettangolo

Capita a tutti, ad un certo punto, di trovarsi di fronte a un problema di geometria. Magari stai aiutando tuo figlio con i compiti, oppure ti serve calcolare il materiale per una mensola triangolare da appendere in casa. E all'improvviso, ti blocchi: come si calcola il perimetro di un triangolo rettangolo? Niente panico! Questo articolo è qui per aiutarti a superare questo ostacolo in modo semplice e chiaro.

Sappiamo che la geometria può sembrare ostica, piena di formule e concetti astratti. Ma la verità è che si applica costantemente nella nostra vita quotidiana. Dal taglio di un pezzo di pizza alla progettazione di un tetto, i triangoli e le loro proprietà sono fondamentali. Imparare a calcolare il perimetro di un triangolo rettangolo, quindi, non è solo un esercizio scolastico, ma un'abilità pratica che può tornarti utile in molte situazioni.

Cos'è un Triangolo Rettangolo?

Prima di tuffarci nel calcolo del perimetro, ripassiamo brevemente cos'è un triangolo rettangolo. Un triangolo rettangolo è un triangolo che ha un angolo retto, ovvero un angolo di 90 gradi. I lati che formano l'angolo retto si chiamano cateti, mentre il lato opposto all'angolo retto si chiama ipotenusa. L'ipotenusa è sempre il lato più lungo del triangolo rettangolo.

Per intenderci, immagina un angolo di una stanza: quello è un angolo retto! Ora, traccia una linea retta dal pavimento al soffitto lungo un lato dell'angolo, e un'altra lungo l'altro lato. Se poi congiungi le due estremità superiori con una linea, hai creato un triangolo rettangolo!

Come Calcolare il Perimetro: Metodo Base

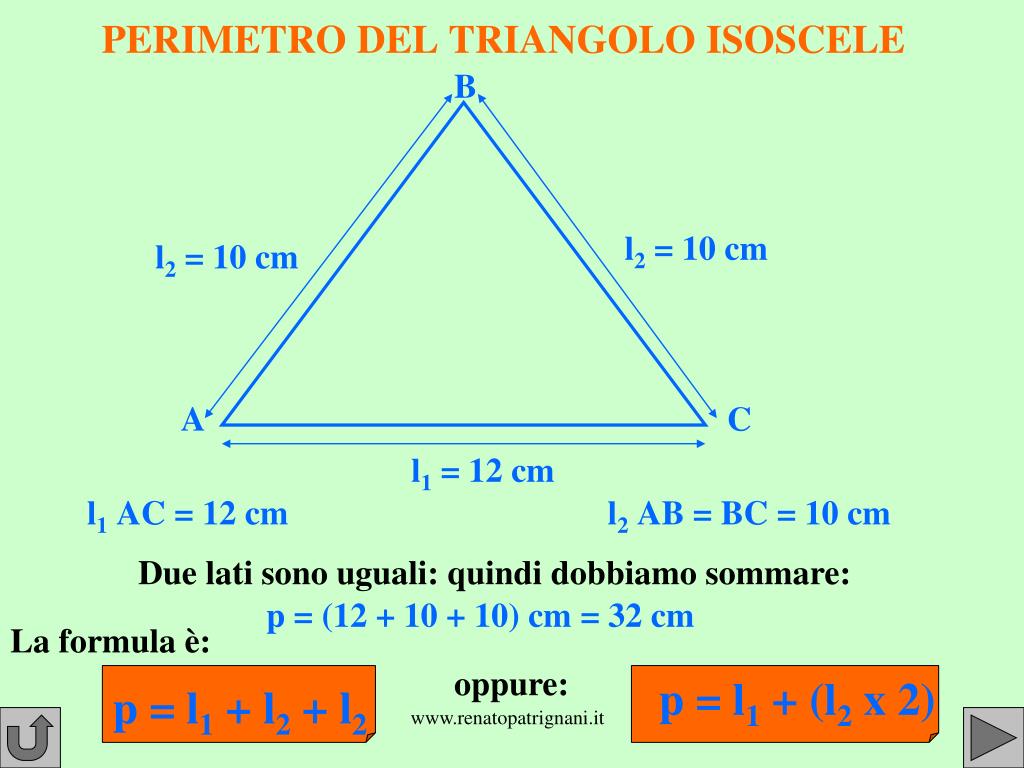
Il perimetro di qualsiasi figura geometrica, compreso il triangolo, è semplicemente la somma delle lunghezze di tutti i suoi lati. Quindi, per calcolare il perimetro di un triangolo rettangolo, abbiamo bisogno di conoscere la lunghezza dei due cateti e dell'ipotenusa. La formula è semplicissima:

Perimetro = cateto 1 + cateto 2 + ipotenusa

Esempio pratico: Supponiamo che un triangolo rettangolo abbia un cateto di 3 cm, un altro cateto di 4 cm e un'ipotenusa di 5 cm. Il suo perimetro sarà:

Perimetro = 3 cm + 4 cm + 5 cm = 12 cm

Semplice, no?

Il Teorema di Pitagora: Quando Manca l'Ipotenusa

Cosa succede se conosciamo solo la lunghezza dei due cateti, ma non quella dell'ipotenusa? Qui entra in gioco un amico prezioso: il Teorema di Pitagora.

Il Teorema di Pitagora afferma che, in un triangolo rettangolo, il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti. In termini matematici:

a² + b² = c²

Dove:

• a e b sono le lunghezze dei cateti
• c è la lunghezza dell'ipotenusa

Come usare il Teorema di Pitagora per trovare l'ipotenusa:

1. Eleva al quadrato la lunghezza di ciascun cateto.
2. Somma i risultati.
3. Calcola la radice quadrata della somma ottenuta. Questo sarà la lunghezza dell'ipotenusa!

Esempio pratico: Immagina di avere un triangolo rettangolo con un cateto di 6 cm e un altro di 8 cm. Vogliamo trovare l'ipotenusa.

1. 6² = 36
2. 8² = 64
3. 36 + 64 = 100
4. √100 = 10

Quindi, l'ipotenusa misura 10 cm. Ora possiamo calcolare il perimetro: 6 cm + 8 cm + 10 cm = 24 cm.

E se Manca un Cateto?

Il Teorema di Pitagora può essere utilizzato anche per trovare la lunghezza di un cateto se conosciamo l'ipotenusa e l'altro cateto. Basta manipolare un po' la formula:

a² = c² - b²

Dove:

• a è il cateto che vogliamo trovare
• b è l'altro cateto
• c è l'ipotenusa

Esempio pratico: Supponiamo di avere un triangolo rettangolo con un'ipotenusa di 13 cm e un cateto di 5 cm. Vogliamo trovare la lunghezza dell'altro cateto.

1. 13² = 169
2. 5² = 25
3. 169 - 25 = 144
4. √144 = 12

Quindi, l'altro cateto misura 12 cm. Il perimetro sarà: 5 cm + 12 cm + 13 cm = 30 cm.

Triangoli Rettangoli Speciali: Un Trucco per Velocizzare i Calcoli

Esistono alcuni tipi di triangoli rettangoli con rapporti fissi tra i lati, che possono semplificare i calcoli. I due più comuni sono:

• Triangolo 3-4-5: È il triangolo rettangolo con i lati che stanno nel rapporto 3:4:5 (es. 3 cm, 4 cm, 5 cm; 6 cm, 8 cm, 10 cm, ecc.). Se conosci la lunghezza di due lati che rientrano in questo rapporto, puoi dedurre la lunghezza del terzo senza usare il Teorema di Pitagora.
• Triangolo 45-45-90: È un triangolo rettangolo isoscele, ovvero con due lati (i cateti) uguali e due angoli di 45 gradi. In questo caso, l'ipotenusa è uguale alla lunghezza del cateto moltiplicata per √2.

Controindicazioni e Approcci Alternativi

Alcune persone potrebbero sostenere che, nell'era della tecnologia, imparare a calcolare il perimetro a mano sia inutile. In fondo, esistono calcolatrici online e app che fanno tutto il lavoro per noi. Questo è parzialmente vero, ma comprendere i principi di base della geometria ti permette di avere una visione più chiara del mondo che ti circonda e di risolvere problemi in modo più efficace, anche quando non hai accesso a un dispositivo elettronico.

Inoltre, a volte potrebbe essere più rapido fare un calcolo mentale veloce che cercare un'app e inserire i dati. La conoscenza è potere, e la capacità di risolvere problemi geometrici di base è un'abilità utile in molte situazioni.

Un approccio alternativo, soprattutto per chi trova difficoltà con le formule, è visualizzare il triangolo e ragionare intuitivamente. Disegnare il triangolo su un foglio di carta può aiutare a comprendere meglio le relazioni tra i lati e a trovare la soluzione.

Applicazioni Pratiche del Calcolo del Perimetro

Come abbiamo detto all'inizio, il calcolo del perimetro di un triangolo rettangolo non è solo un esercizio teorico. Ecco alcuni esempi di come può essere utile nella vita reale:

• Costruzione: Calcolare la quantità di materiale necessaria per costruire un tetto, una scala o una struttura triangolare.
• Giardinaggio: Progettare un'aiuola triangolare e calcolare la quantità di bordura necessaria.
• Fai da te: Costruire una mensola triangolare, un supporto per piante o un elemento decorativo.
• Navigazione: Utilizzare la trigonometria per calcolare distanze e angoli, che si basano sui principi dei triangoli rettangoli.

Questi sono solo alcuni esempi, ma le applicazioni sono infinite! Imparare a calcolare il perimetro di un triangolo rettangolo ti apre un mondo di possibilità e ti permette di affrontare con sicurezza molti problemi pratici.

In conclusione, calcolare il perimetro di un triangolo rettangolo è un'operazione semplice che richiede la conoscenza della lunghezza dei suoi lati. Se manca l'ipotenusa (o un cateto), puoi utilizzare il Teorema di Pitagora per calcolarla. Ricorda, la geometria non è un'entità astratta, ma uno strumento potente che può aiutarti a risolvere problemi reali. Quindi, non aver paura di sperimentare e di mettere in pratica quello che hai imparato!

Ora, prova a risolvere questo problema: hai un triangolo rettangolo con un cateto di 7 cm e un'ipotenusa di 25 cm. Qual è il suo perimetro? Metti alla prova le tue nuove competenze!