Come Capire Se Una Funzione è Crescente O Decrescente

Ti sei mai chiesto come capire se una funzione matematica sta salendo verso l'alto, come una montagna che conquistiamo passo dopo passo, o se sta scendendo verso il basso, come una discesa mozzafiato con gli sci? Capire se una funzione è crescente o decrescente è fondamentale in tantissimi ambiti, dalla fisica all'economia, e non è così difficile come sembra! Questo articolo è pensato per chiunque abbia una conoscenza base di matematica, anche solo a livello scolastico, e vuole imparare a identificare il comportamento crescente o decrescente di una funzione in modo semplice e intuitivo.

Comprendere le Definizioni Fondamentali

Prima di addentrarci nei metodi pratici, definiamo cosa intendiamo per funzione crescente e decrescente. Immagina una funzione come un percorso su una mappa.

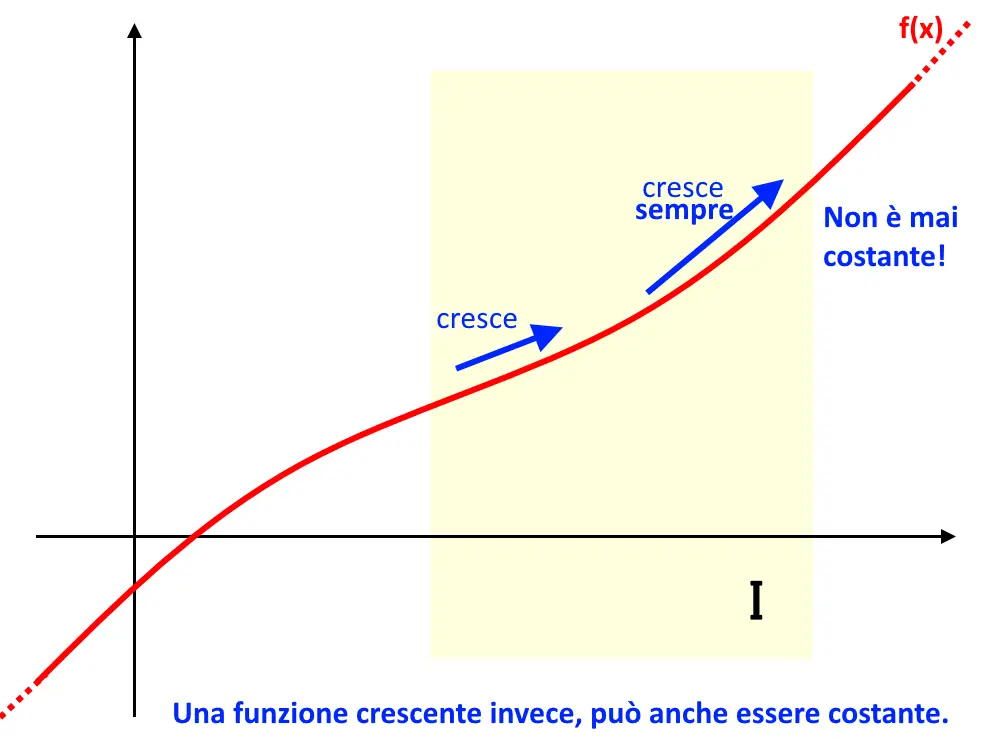
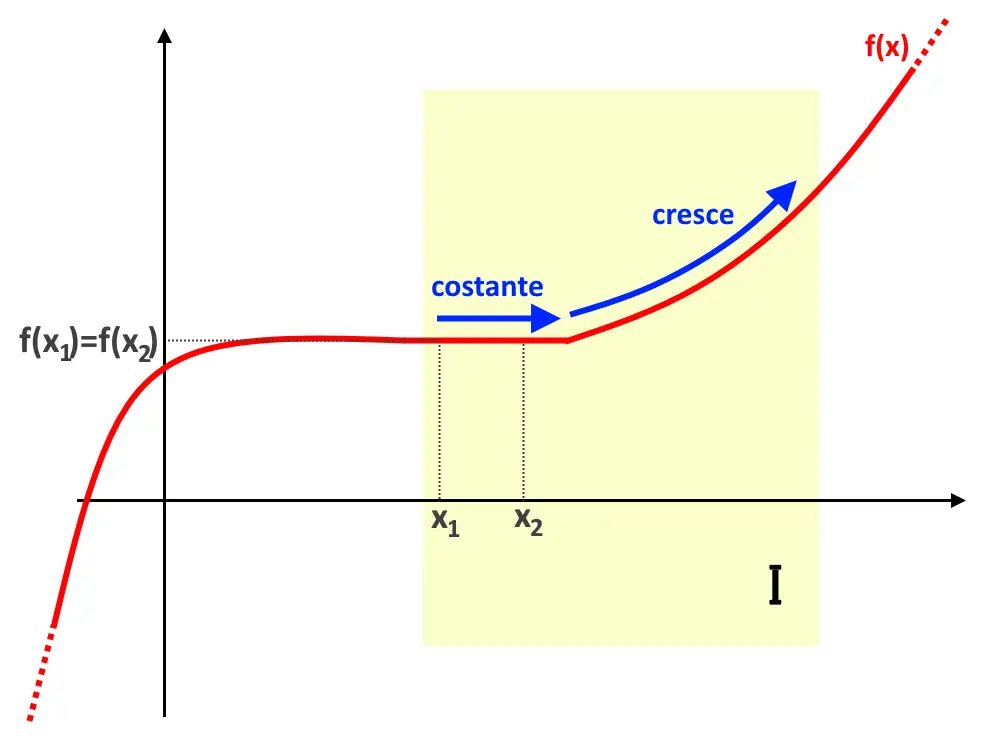
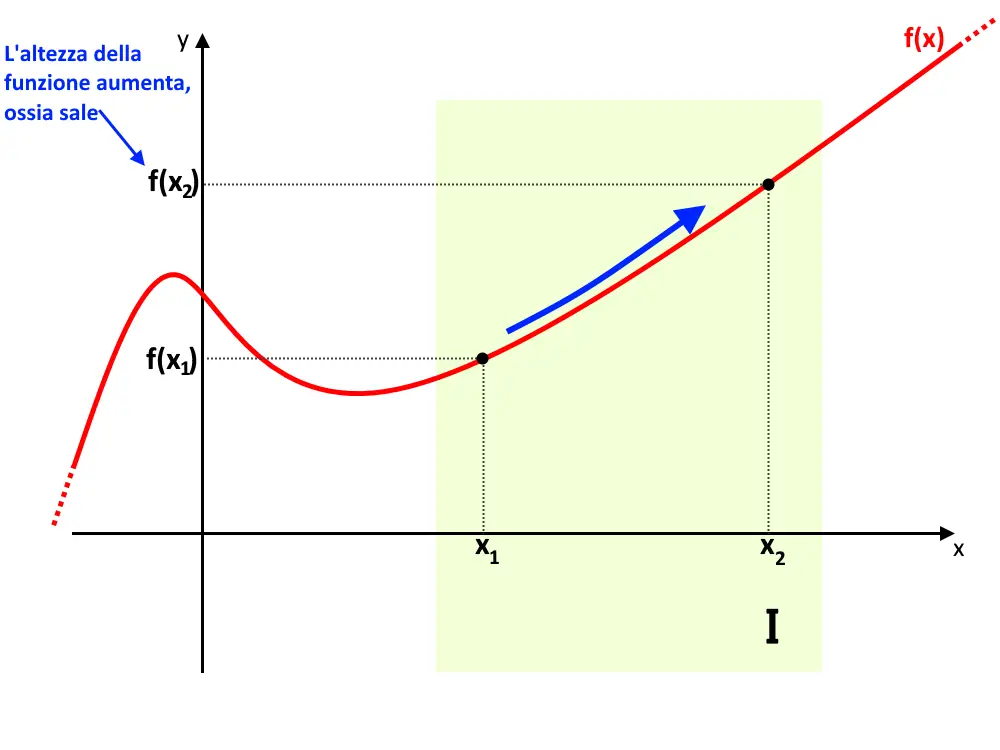
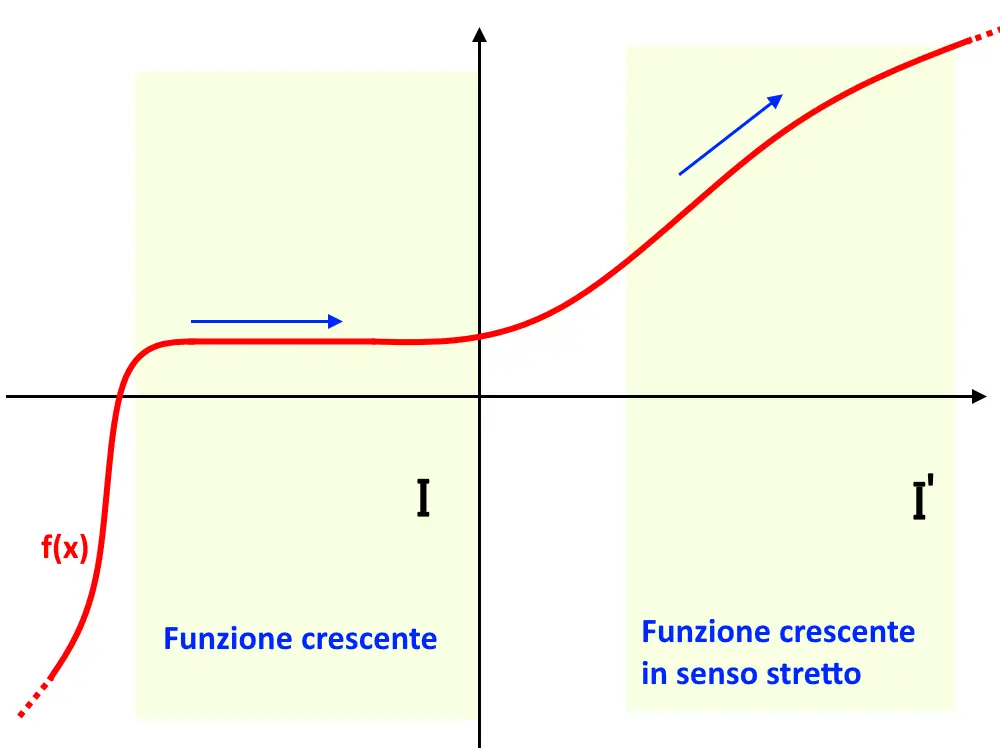
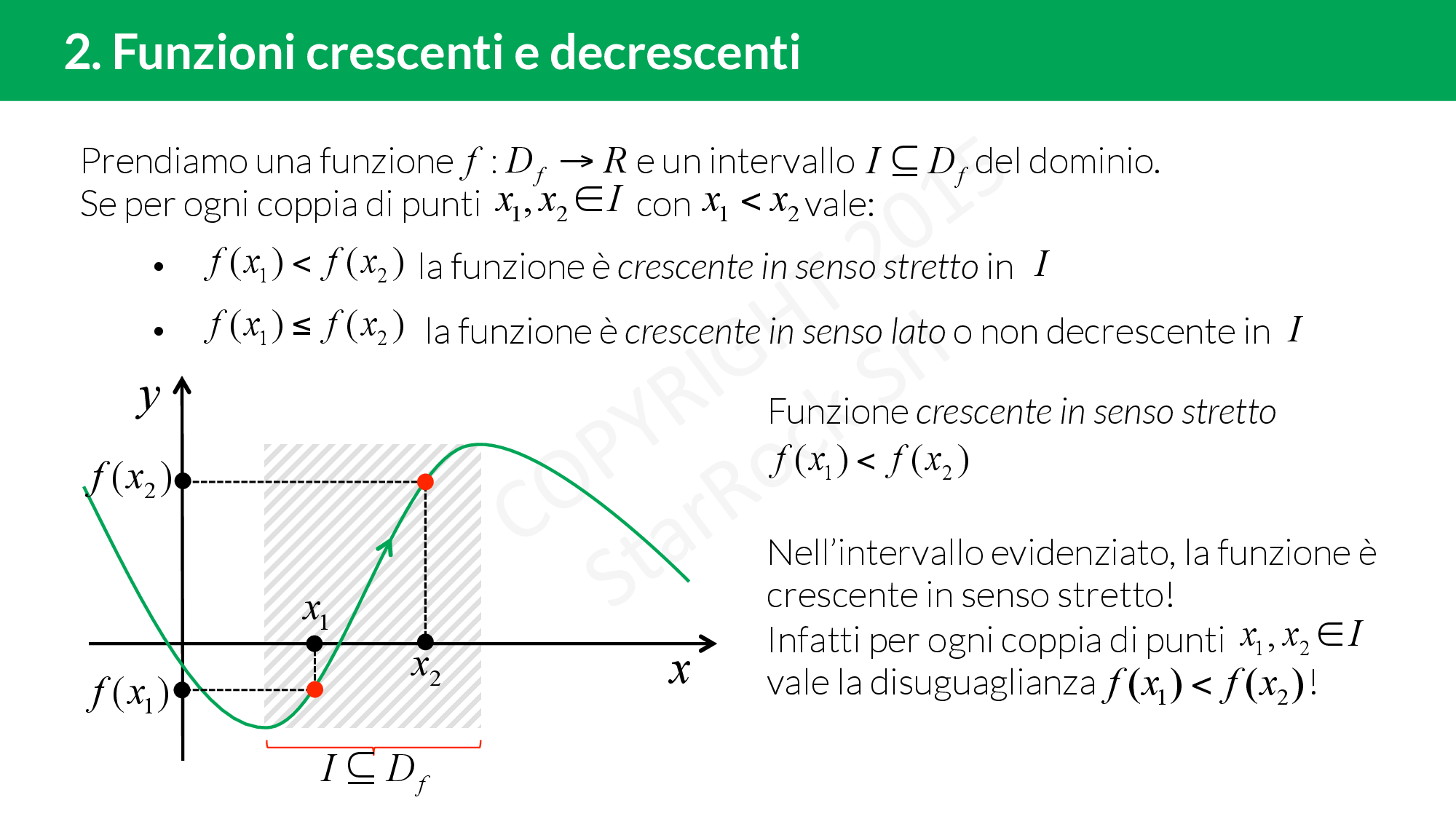
Funzione Crescente: Se, mentre ti sposti da sinistra a destra lungo il grafico della funzione, sali, allora la funzione è crescente. Formalmente, una funzione f(x) è crescente in un intervallo se per ogni x₁ e x₂ nell'intervallo, con x₁ < x₂, si ha f(x₁) ≤ f(x₂). Se f(x₁) < f(x₂), la funzione è strettamente crescente.
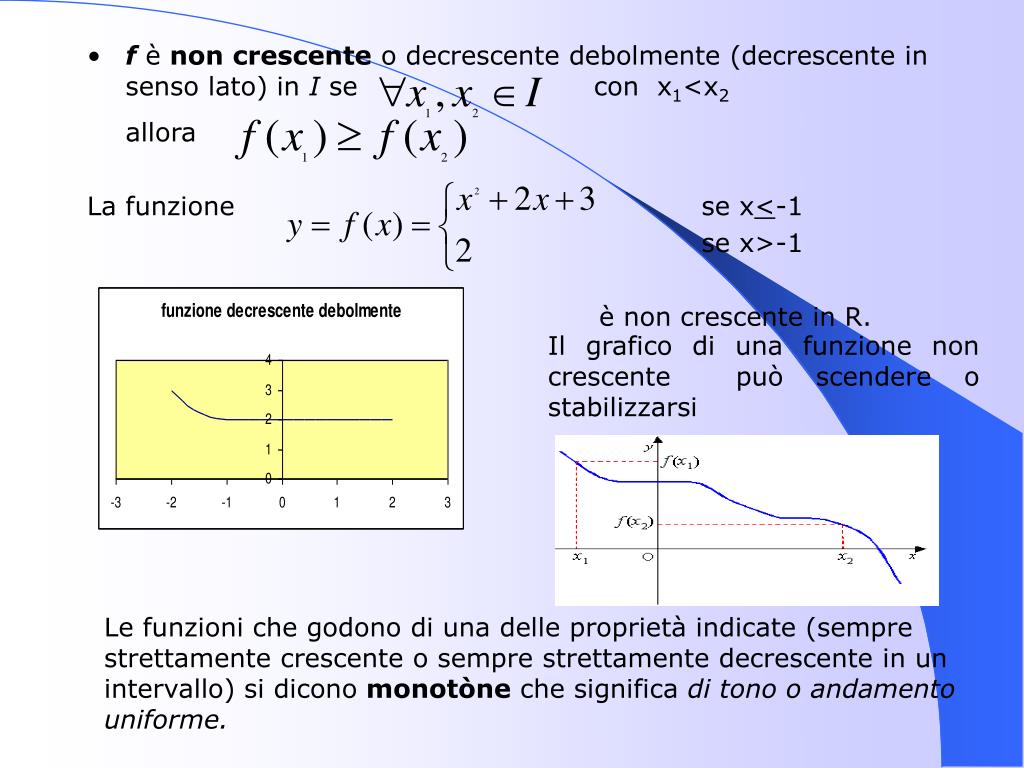
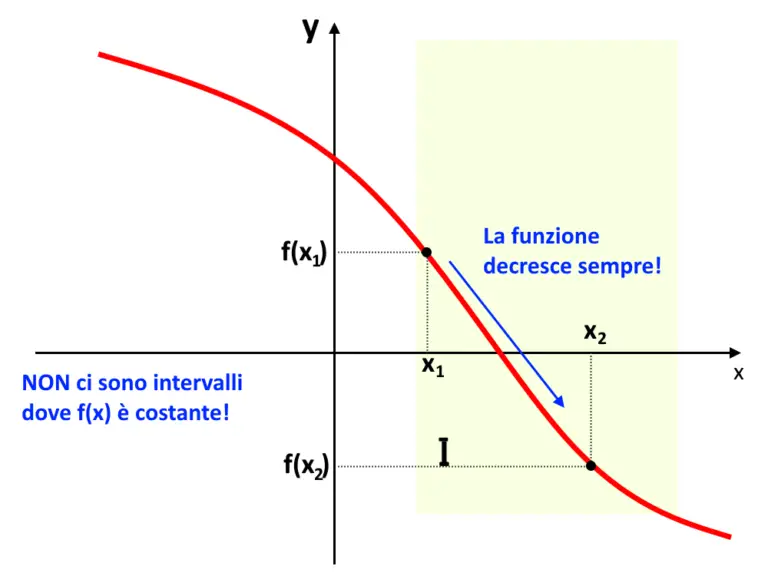
Funzione Decrescente: Se, mentre ti sposti da sinistra a destra lungo il grafico della funzione, scendi, allora la funzione è decrescente. Formalmente, una funzione f(x) è decrescente in un intervallo se per ogni x₁ e x₂ nell'intervallo, con x₁ < x₂, si ha f(x₁) ≥ f(x₂). Se f(x₁) > f(x₂), la funzione è strettamente decrescente.

In parole povere, crescente significa che "più vai avanti, più il valore della funzione aumenta (o rimane uguale)" e decrescente significa che "più vai avanti, più il valore della funzione diminuisce (o rimane uguale)".

Metodo Grafico: Un'Immagine Vale Più di Mille Parole

Il modo più intuitivo per capire se una funzione è crescente o decrescente è osservare il suo grafico.

Esempio: Disegna una retta che sale da sinistra a destra. Questa è una funzione crescente. Disegna una retta che scende da sinistra a destra. Questa è una funzione decrescente.

Analizza il grafico e individua gli intervalli in cui:

La funzione "sale": in questi intervalli è crescente.
La funzione "scende": in questi intervalli è decrescente.
La funzione è piatta (orizzontale): in questi intervalli è costante (né crescente né decrescente).

Questo metodo è particolarmente utile per funzioni complesse, dove l'analisi algebrica potrebbe essere più difficile. Tuttavia, il grafico deve essere accurato per poter trarre conclusioni corrette.

Metodo Analitico: Usare le Derivate a Nostro Vantaggio

Il metodo analitico si basa sull'utilizzo delle derivate. Se hai familiarità con il concetto di derivata, sai che rappresenta la pendenza della retta tangente al grafico della funzione in un determinato punto. Questa informazione è cruciale per determinare la crescita o decrescita di una funzione.

La Derivata Prima e la Monotonia

La derivata prima, indicata con f'(x), ci fornisce informazioni sulla pendenza della funzione in ogni punto.

f'(x) > 0: Se la derivata prima è positiva in un intervallo, significa che la retta tangente ha pendenza positiva, quindi la funzione è crescente in quell'intervallo.
f'(x) < 0: Se la derivata prima è negativa in un intervallo, significa che la retta tangente ha pendenza negativa, quindi la funzione è decrescente in quell'intervallo.
f'(x) = 0: Se la derivata prima è uguale a zero in un punto, significa che la retta tangente è orizzontale. Questo punto è un punto stazionario, che potrebbe essere un massimo locale, un minimo locale o un punto di flesso.

Come Applicare il Metodo Analitico:

Calcola la derivata prima f'(x) della funzione f(x).
Trova i punti critici: Risolvi l'equazione f'(x) = 0 per trovare i valori di x in cui la derivata prima è uguale a zero. Questi sono i punti critici.
Analizza il segno della derivata prima in intervalli: Dividi la retta reale in intervalli usando i punti critici. Scegli un valore di x all'interno di ciascun intervallo e calcola f'(x) in quel punto. Se f'(x) è positiva, la funzione è crescente in quell'intervallo; se f'(x) è negativa, la funzione è decrescente in quell'intervallo.

Esempio: Consideriamo la funzione f(x) = x². La derivata prima è f'(x) = 2x. Impostando f'(x) = 0, troviamo il punto critico x = 0. Ora, analizziamo il segno di f'(x) in due intervalli:

Per x < 0 (ad esempio, x = -1), f'(-1) = -2, quindi la funzione è decrescente.
Per x > 0 (ad esempio, x = 1), f'(1) = 2, quindi la funzione è crescente.

Questo conferma che la parabola f(x) = x² è decrescente per x < 0 e crescente per x > 0, con un minimo in x = 0.

Punti Critici e Loro Importanza

Come abbiamo accennato, i punti critici (dove f'(x) = 0 o f'(x) non esiste) sono fondamentali per determinare gli intervalli di crescita e decrescita di una funzione. Possono rappresentare:

Massimi Locali: La funzione passa da crescente a decrescente.
Minimi Locali: La funzione passa da decrescente a crescente.
Punti di Flesso: La funzione cambia la concavità (da concava verso l'alto a concava verso il basso o viceversa). In un punto di flesso la derivata seconda cambia segno.

L'analisi dei punti critici, insieme al segno della derivata prima, ci permette di disegnare un quadro completo del comportamento di una funzione.

Esercizi Pratici per Allenare l'Occhio (e la Mente!)

Ora che abbiamo visto la teoria, mettiamola in pratica! Prova a determinare gli intervalli di crescita e decrescita delle seguenti funzioni:

f(x) = x³ - 3x
f(x) = e^x
f(x) = sin(x) (in un intervallo di 2π)

Per ogni funzione, segui questi passaggi:

Calcola la derivata prima f'(x).
Trova i punti critici (f'(x) = 0).
Analizza il segno di f'(x) negli intervalli definiti dai punti critici.
Concludi determinando gli intervalli di crescita e decrescita.

Errori Comuni da Evitare

Ecco alcuni errori comuni che è importante evitare quando si analizza la crescita e decrescita di una funzione:

Confondere f(x) con f'(x): Ricorda che f(x) rappresenta il valore della funzione, mentre f'(x) rappresenta la sua pendenza.
Ignorare i punti in cui f'(x) non esiste: Questi punti possono essere importanti, soprattutto in funzioni con valori assoluti o radici.
Trarre conclusioni affrettate: È fondamentale analizzare il segno della derivata prima in tutti gli intervalli definiti dai punti critici.
Basarsi solo sul grafico senza confermare analiticamente: Il grafico può essere utile, ma è sempre meglio confermare i risultati con il metodo analitico.

Applicazioni Pratiche: Oltre la Matematica Pura

Capire se una funzione è crescente o decrescente non è solo un esercizio teorico. Ha applicazioni pratiche in molti campi:

Economia: Analizzare la crescita o decrescita dei profitti, dei costi o della domanda.
Fisica: Studiare il movimento di un oggetto, la variazione della temperatura o la velocità di una reazione chimica.
Ingegneria: Ottimizzare i processi, progettare strutture resistenti e controllare i sistemi.
Informatica: Analizzare l'efficienza degli algoritmi e la velocità di elaborazione.

Ad esempio, un'azienda potrebbe utilizzare l'analisi delle derivate per determinare il prezzo ottimale di un prodotto, massimizzando i profitti. Un ingegnere potrebbe usarla per calcolare la curvatura di un ponte, garantendone la stabilità.

Conclusione: Un'Abilità Fondamentale per il Successo

Speriamo che questo articolo ti abbia fornito gli strumenti necessari per capire se una funzione è crescente o decrescente. Ricorda, la chiave è praticare! Più esercizi farai, più diventerai abile nell'analizzare le funzioni e nel comprendere il loro comportamento. Questo tipo di analisi non solo rafforza la tua comprensione della matematica, ma ti fornisce anche una base solida per affrontare problemi in una vasta gamma di discipline. Quindi, prendi carta e penna, e inizia a esplorare il meraviglioso mondo delle funzioni!