Come Calcolare L'ipotenusa Di Un Triangolo Rettangolo Conoscendo I Cateti

Ti sei mai trovato di fronte a un problema geometrico in cui dovevi calcolare la lunghezza di un lato di un triangolo rettangolo? Magari stavi progettando un tetto, costruendo una rampa, o semplicemente aiutando tuo figlio con i compiti. Capita spesso! La geometria, a volte, può sembrare ostica, ma con gli strumenti giusti e un po' di pazienza, si rivela accessibile e, persino, affascinante.

Questo articolo è pensato per te, che magari hai dimenticato le basi della trigonometria o che semplicemente cerchi una guida chiara e concisa. Affronteremo insieme il Teorema di Pitagora, lo strumento fondamentale per calcolare l'ipotenusa di un triangolo rettangolo conoscendo la lunghezza dei suoi cateti. Non preoccuparti, non useremo formule complicate senza spiegazioni. Ti accompagnerò passo dopo passo, con esempi pratici e analogie intuitive.

Il Teorema di Pitagora: La Chiave per Risolvere il Problema

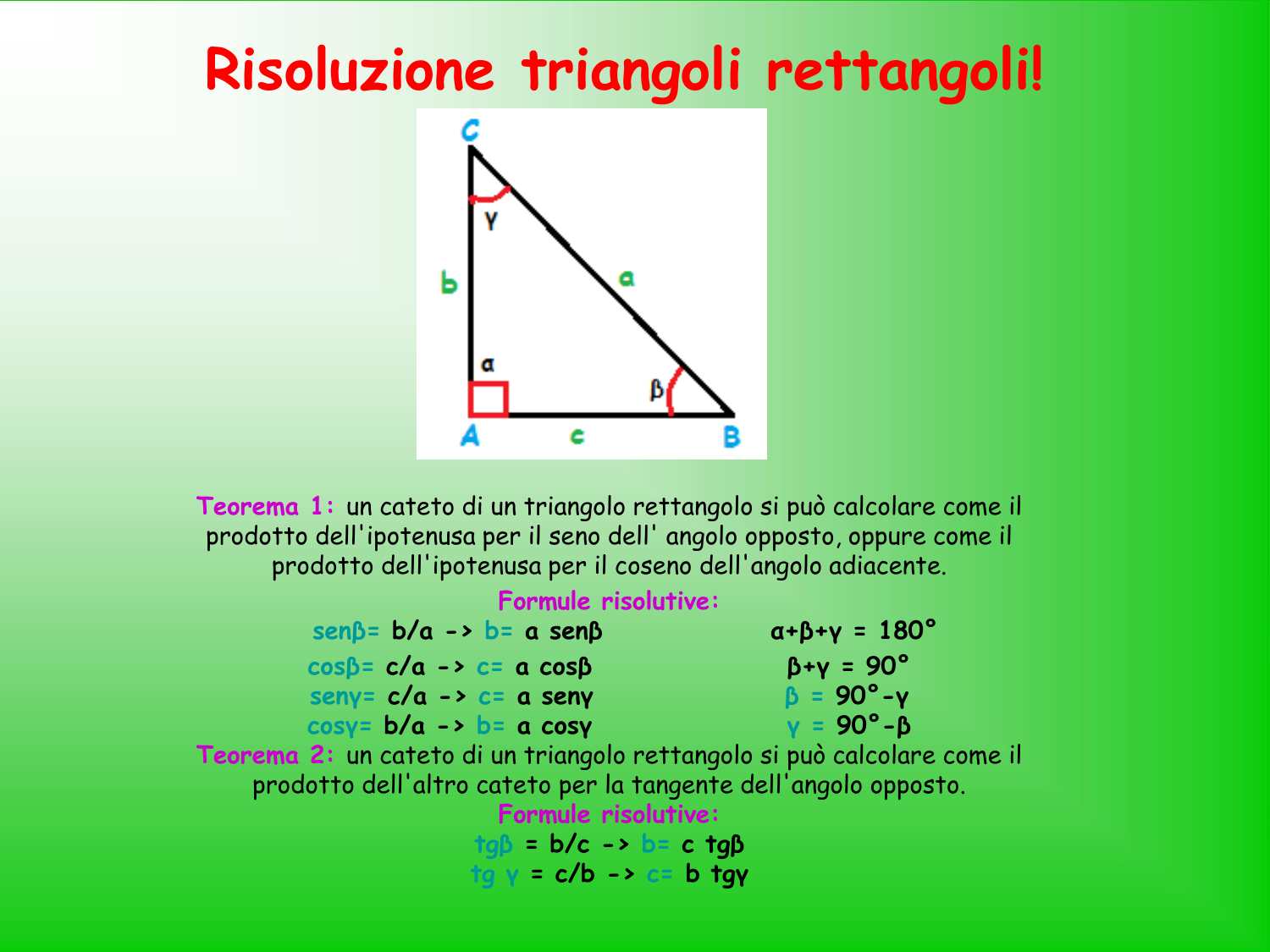
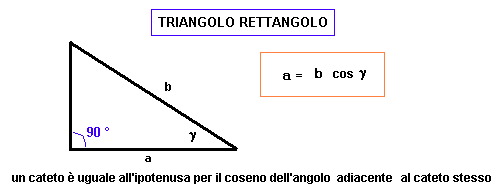
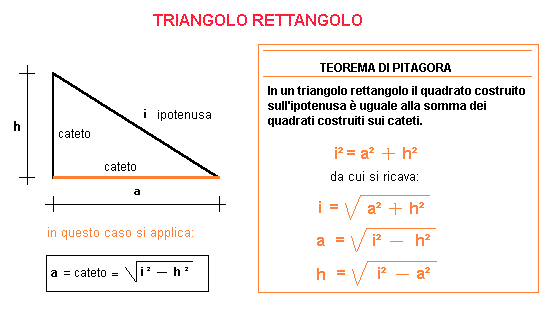
Il Teorema di Pitagora è una delle pietre miliari della geometria euclidea. Afferma che in un triangolo rettangolo, l'area del quadrato costruito sull'ipotenusa (il lato opposto all'angolo retto) è uguale alla somma delle aree dei quadrati costruiti sui cateti (i due lati che formano l'angolo retto).

Può sembrare complicato detto così, ma in realtà è molto semplice. Immagina di avere un triangolo rettangolo. Ora, disegna un quadrato su ciascun lato del triangolo. Il Teorema di Pitagora dice che se sommi l'area dei due quadrati più piccoli (quelli costruiti sui cateti), otterrai esattamente l'area del quadrato più grande (quello costruito sull'ipotenusa).

Matematicamente, questo si traduce nella seguente formula:

a² + b² = c²

Dove:

• a e b sono le lunghezze dei cateti.
• c è la lunghezza dell'ipotenusa.

Questa formula è il cuore di tutto il nostro ragionamento. Una volta che conosci le lunghezze dei cateti (a e b), puoi facilmente calcolare la lunghezza dell'ipotenusa (c).

Come Calcolare l'Ipotenusa: Passo Dopo Passo

Ora vediamo come applicare concretamente il Teorema di Pitagora per calcolare l'ipotenusa:

1. Identifica i cateti: Assicurati di conoscere la lunghezza di entrambi i cateti del triangolo rettangolo. Ricorda, i cateti sono i due lati che formano l'angolo retto.
2. Eleva al quadrato i cateti: Calcola il quadrato di ciascun cateto. Ad esempio, se un cateto è lungo 3 cm, il suo quadrato sarà 3 cm * 3 cm = 9 cm².
3. Somma i quadrati dei cateti: Somma i due risultati ottenuti al punto precedente. Questo ti darà la somma delle aree dei quadrati costruiti sui cateti.
4. Calcola la radice quadrata: Calcola la radice quadrata della somma ottenuta al punto precedente. Il risultato sarà la lunghezza dell'ipotenusa.

Esempio pratico:

Supponiamo di avere un triangolo rettangolo con i cateti che misurano 3 cm e 4 cm. Calcoliamo l'ipotenusa:

• a = 3 cm
• b = 4 cm
• a² = 3² = 9 cm²
• b² = 4² = 16 cm²
• a² + b² = 9 cm² + 16 cm² = 25 cm²
• c = √25 cm² = 5 cm

Quindi, l'ipotenusa del triangolo rettangolo è lunga 5 cm.

Un'Analogia per Comprendere Meglio

Immagina di dover attraversare un campo rettangolare. Potresti camminare lungo due lati del campo (i cateti), oppure potresti prendere la scorciatoia in diagonale (l'ipotenusa). Il Teorema di Pitagora ti dice esattamente quanto è più corta la scorciatoia rispetto al percorso lungo i due lati. In altre parole, ti permette di calcolare la distanza in linea retta tra due punti, anche se devi muoverti lungo due direzioni perpendicolari.

Applicazioni Reali del Teorema di Pitagora

Il Teorema di Pitagora non è solo un concetto astratto. Ha applicazioni pratiche in molti campi, tra cui:

• Costruzioni: Calcolare la lunghezza delle travi, l'inclinazione dei tetti, o la diagonale di un edificio.
• Navigazione: Determinare la distanza tra due punti sulla mappa, considerando la latitudine e la longitudine.
• Ingegneria: Progettare ponti, edifici, e altre strutture.
• Fisica: Calcolare la risultante di due vettori perpendicolari.
• Videogiochi e Grafica Computerizzata: Determinare le distanze e le posizioni degli oggetti nello spazio tridimensionale.

Come vedi, il Teorema di Pitagora è uno strumento versatile e potente che ci aiuta a risolvere problemi concreti in molti ambiti della vita.

Controindicazioni e Limiti del Teorema di Pitagora

È importante sottolineare che il Teorema di Pitagora si applica solo ai triangoli rettangoli. Non può essere utilizzato per calcolare i lati di triangoli acutangoli (con tutti gli angoli acuti) o ottusangoli (con un angolo ottuso). Per questi tipi di triangoli, è necessario utilizzare il teorema dei coseni o il teorema dei seni.

Alcuni potrebbero sostenere che l'apprendimento del Teorema di Pitagora è obsoleto nell'era delle calcolatrici e dei computer. Tuttavia, la comprensione dei principi fondamentali della geometria è essenziale per sviluppare il pensiero logico e la capacità di risolvere problemi. Anche se non dovrai mai calcolare manualmente l'ipotenusa di un triangolo, la conoscenza del Teorema di Pitagora ti aiuterà a comprendere meglio il mondo che ti circonda e ad affrontare sfide più complesse.

Strumenti Online per Verificare i Tuoi Calcoli

Se vuoi essere sicuro dei tuoi calcoli, puoi utilizzare uno dei tanti calcolatori online disponibili gratuitamente. Basta inserire le lunghezze dei cateti e il calcolatore ti fornirà immediatamente la lunghezza dell'ipotenusa. Questi strumenti sono utili per verificare i tuoi risultati e per velocizzare il processo di calcolo, ma non dovrebbero sostituire la comprensione del Teorema di Pitagora.

In Sintesi: Punti Chiave da Ricordare

Ricapitoliamo i punti chiave per calcolare l'ipotenusa di un triangolo rettangolo:

• Il Teorema di Pitagora afferma che a² + b² = c², dove a e b sono i cateti e c è l'ipotenusa.
• Eleva al quadrato la lunghezza di ciascun cateto.
• Somma i due risultati ottenuti.
• Calcola la radice quadrata della somma. Il risultato è la lunghezza dell'ipotenusa.
• Il Teorema di Pitagora si applica solo ai triangoli rettangoli.

Con un po' di pratica, sarai in grado di calcolare l'ipotenusa di un triangolo rettangolo in modo rapido e preciso. Ricorda, la chiave è la comprensione del Teorema di Pitagora e la sua applicazione pratica.

Spero che questa guida ti sia stata utile. Hai trovato facile da seguire la spiegazione? Prova ad applicare il Teorema di Pitagora ad un problema reale e vedrai come la geometria può essere uno strumento potente e divertente!