Come Calcolare L Altezza Di Un Rettangolo

Capita a tutti, prima o poi, di trovarsi di fronte a un problema di geometria che sembra insormontabile. Magari stai ristrutturando casa, devi incorniciare un quadro, oppure semplicemente aiutare tuo figlio con i compiti. E improvvisamente, eccolo lì: il rettangolo. Sembra una figura semplice, ma calcolare l'altezza, a volte, può diventare un vero rompicapo. Non preoccuparti, non sei solo! Questo articolo è pensato proprio per te, per guidarti passo dopo passo attraverso le varie situazioni in cui potresti aver bisogno di calcolare l'altezza di un rettangolo, rendendo il processo il più semplice e chiaro possibile.

Sappiamo che la matematica può intimidire, ma credici, con un po' di chiarezza e i giusti strumenti, sarai in grado di affrontare qualsiasi sfida geometrica ti si presenti. L'obiettivo qui è darti una comprensione pratica, non solo teorica, di come calcolare l'altezza di un rettangolo in diverse circostanze.

Comprendere le Basi del Rettangolo

Prima di tuffarci nei calcoli, facciamo un breve ripasso delle caratteristiche fondamentali del rettangolo:

• Quattro lati: Due lati sono uguali in lunghezza (le basi) e gli altri due sono uguali in lunghezza (le altezze).
• Quattro angoli retti: Ogni angolo del rettangolo misura 90 gradi.
• Area: Lo spazio racchiuso all'interno del rettangolo.
• Perimetro: La somma della lunghezza di tutti i lati.

Questi concetti base sono fondamentali per capire come calcolare l'altezza. Se anche solo uno di questi elementi ti risulta poco chiaro, prenditi un momento per rivederlo. Ti sarà d'aiuto!

Metodo 1: Conoscendo l'Area e la Base

Questo è il caso più comune. Se conosci l'area (A) e la base (b) del rettangolo, calcolare l'altezza (h) è semplicissimo. Ricorda che l'area di un rettangolo si calcola con la formula:

A = b * h

Per trovare l'altezza, basta dividere l'area per la base:

h = A / b

Esempio pratico: Immagina di dover tappezzare una parete rettangolare. Hai misurato l'area della parete, che è di 15 metri quadrati, e sai che la base (la larghezza) è di 3 metri. Quanto è alta la parete?

h = 15 m² / 3 m = 5 m

La parete è alta 5 metri. Facile, no?

Cosa fare se le unità di misura non sono coerenti?

Un errore comune è dimenticarsi di convertire le unità di misura. Se l'area è in metri quadrati (m²) e la base è in centimetri (cm), devi prima convertire tutto nella stessa unità di misura. Ad esempio, converti i centimetri in metri dividendo per 100.

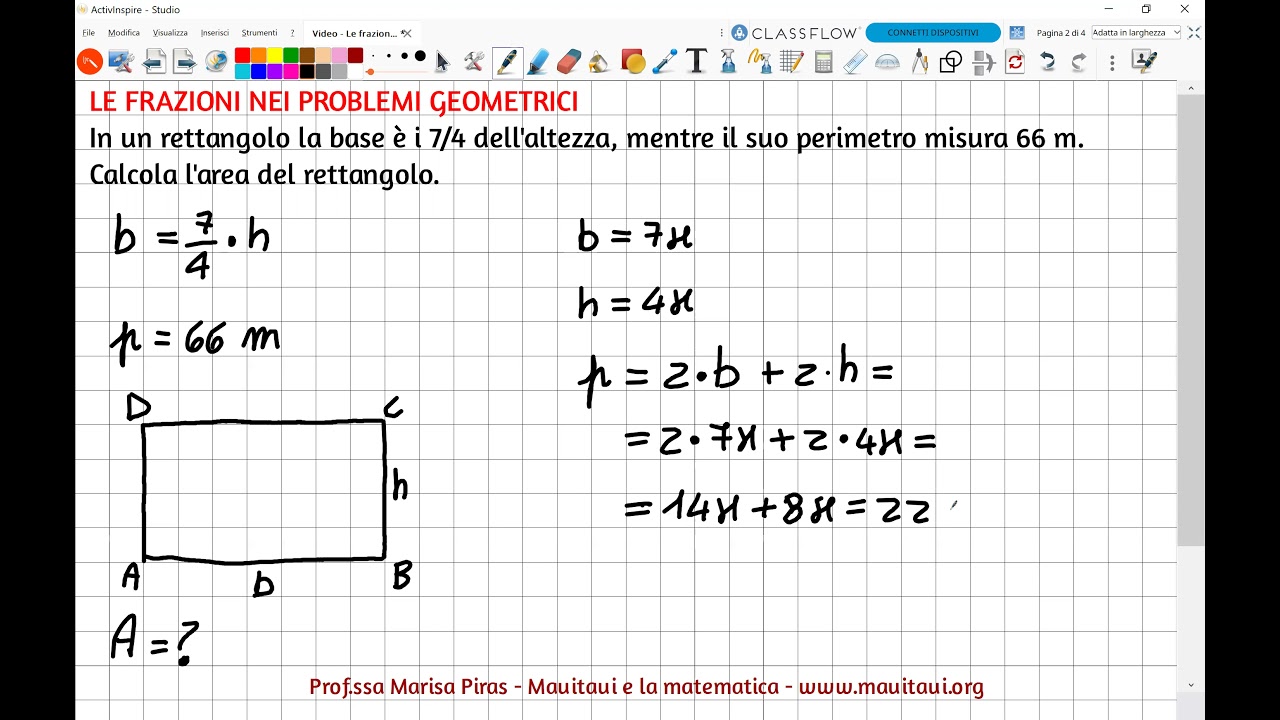
Metodo 2: Conoscendo il Perimetro e la Base

Un altro scenario possibile è conoscere il perimetro (P) e la base (b) del rettangolo. Il perimetro di un rettangolo si calcola con la formula:

P = 2 * (b + h)

Per trovare l'altezza, dobbiamo manipolare un po' la formula:

1. Dividi il perimetro per 2: P / 2 = b + h
2. Sottrai la base da entrambi i lati: h = (P / 2) - b

Esempio pratico: Hai un rettangolo con un perimetro di 20 centimetri e una base di 6 centimetri. Quanto è alta il rettangolo?

h = (20 cm / 2) - 6 cm = 10 cm - 6 cm = 4 cm

L'altezza del rettangolo è di 4 centimetri.

Un piccolo trucco: visualizzare il problema

A volte, visualizzare il problema può aiutarti a capire meglio la formula. Immagina di "aprire" il rettangolo e stenderlo in una linea retta. Il perimetro è la lunghezza di questa linea. Dividendo il perimetro per due, ottieni la somma della base e dell'altezza. Quindi, sottrarre la base ti darà l'altezza.

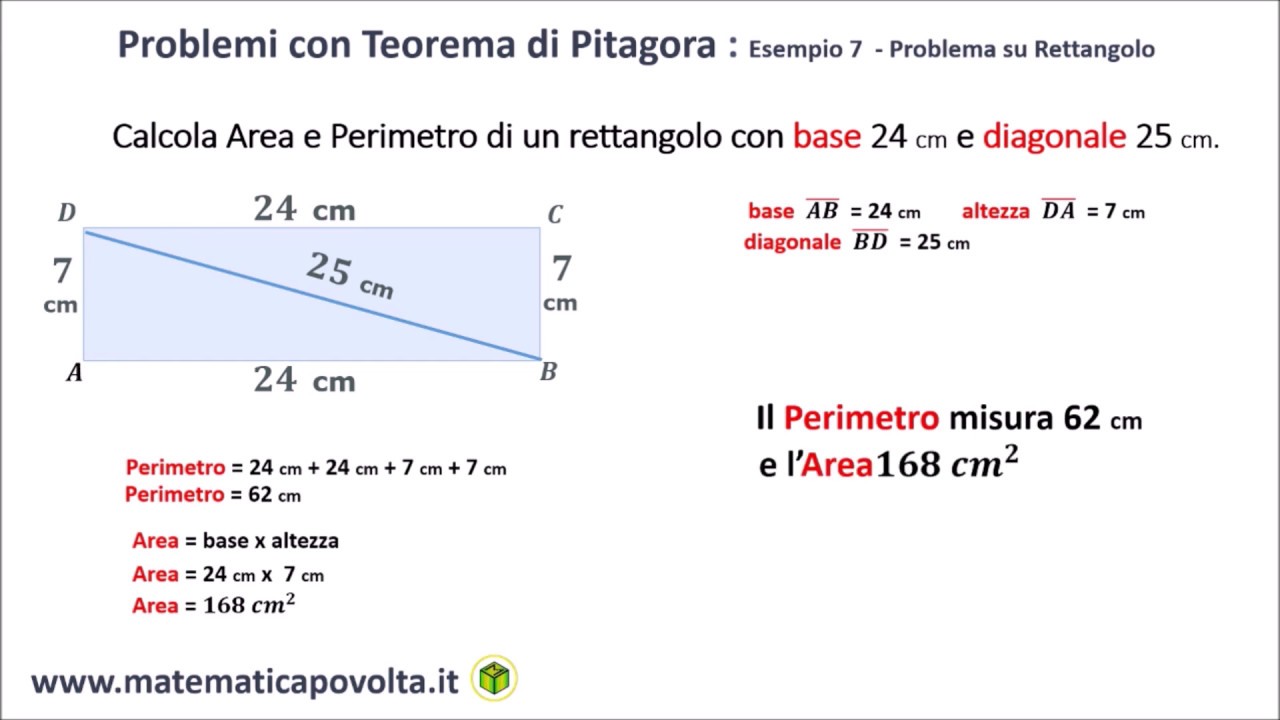
Metodo 3: Conoscendo la Diagonale e la Base (Teorema di Pitagora)

Se conosci la lunghezza della diagonale (d) e della base (b) del rettangolo, puoi utilizzare il teorema di Pitagora per calcolare l'altezza (h). Ricorda che il teorema di Pitagora afferma che in un triangolo rettangolo (e un rettangolo contiene due triangoli rettangoli!), il quadrato dell'ipotenusa (il lato più lungo, in questo caso la diagonale) è uguale alla somma dei quadrati degli altri due lati (la base e l'altezza).

d² = b² + h²

Per trovare l'altezza, dobbiamo riorganizzare la formula:

h² = d² - b²

h = √(d² - b²)

Esempio pratico: Un rettangolo ha una diagonale di 13 centimetri e una base di 12 centimetri. Quanto è alta il rettangolo?

h = √(13² cm² - 12² cm²) = √(169 cm² - 144 cm²) = √(25 cm²) = 5 cm

L'altezza del rettangolo è di 5 centimetri.

Attenzione ai quadrati!

Assicurati di calcolare correttamente i quadrati della diagonale e della base prima di sottrarli. Un errore comune è dimenticarsi di elevare al quadrato i numeri.

Affrontare le Difficoltà Comuni

Ecco alcune difficoltà che potresti incontrare e come superarle:

• Dimenticare le unità di misura: Scrivi sempre le unità di misura accanto ai numeri durante i calcoli. Questo ti aiuterà a evitare errori di conversione.
• Confondere le formule: Scrivi le formule su un foglio e tienile a portata di mano. Rivedile prima di iniziare a calcolare.
• Errori di calcolo: Controlla attentamente i tuoi calcoli. Se hai difficoltà, usa una calcolatrice.
• Paura della matematica: La matematica può sembrare difficile, ma con la pratica diventa più facile. Non arrenderti!

Il Lato Pratico: Perché è Importante Saper Calcolare l'Altezza di un Rettangolo?

Oltre ai compiti di scuola, la capacità di calcolare l'altezza di un rettangolo ha diverse applicazioni pratiche nella vita di tutti i giorni:

• Ristrutturazione e design d'interni: Calcolare la quantità di materiale necessario per pavimenti, pareti, tende, etc.
• Lavori di falegnameria: Costruire mobili, mensole, cornici, etc.
• Giardinaggio: Progettare aiuole, recinzioni, etc.
• Arte e artigianato: Creare opere d'arte, incorniciare quadri, etc.
• Risoluzione di problemi quotidiani: Organizzare lo spazio, calcolare le dimensioni di un pacco per la spedizione, etc.

Quindi, imparare a calcolare l'altezza di un rettangolo non è solo un esercizio matematico, ma un'abilità utile che può semplificarti la vita in molte situazioni.

Considerazioni Finali e Controargomentazioni

Alcuni potrebbero sostenere che, nell'era digitale, con calcolatrici e app a portata di mano, imparare a calcolare manualmente l'altezza di un rettangolo sia obsoleto. Non siamo d'accordo! Comprendere i principi matematici alla base di queste figure geometriche rafforza il pensiero logico, la capacità di problem-solving e la comprensione del mondo che ci circonda. Inoltre, avere questa conoscenza di base ti rende meno dipendente dalla tecnologia e più autonomo nel risolvere problemi pratici.

Un altro controargomento potrebbe essere che esistono software CAD (Computer-Aided Design) che possono calcolare automaticamente le dimensioni di un rettangolo. Questo è vero, ma questi software sono spesso complessi e costosi. Per calcoli semplici, la conoscenza delle formule di base è più che sufficiente.

Speriamo che questa guida ti abbia fornito gli strumenti e la fiducia necessari per affrontare qualsiasi problema legato al calcolo dell'altezza di un rettangolo. Ricorda, la chiave è la pratica. Più esercizi farai, più diventerai bravo. E non aver paura di chiedere aiuto se ti blocchi! Ci sono molte risorse online e offline a tua disposizione.

Ora, prova a mettere in pratica quello che hai imparato. Hai in mente qualche progetto in cui potresti applicare queste conoscenze? Qual è la prossima sfida geometrica che vuoi affrontare?