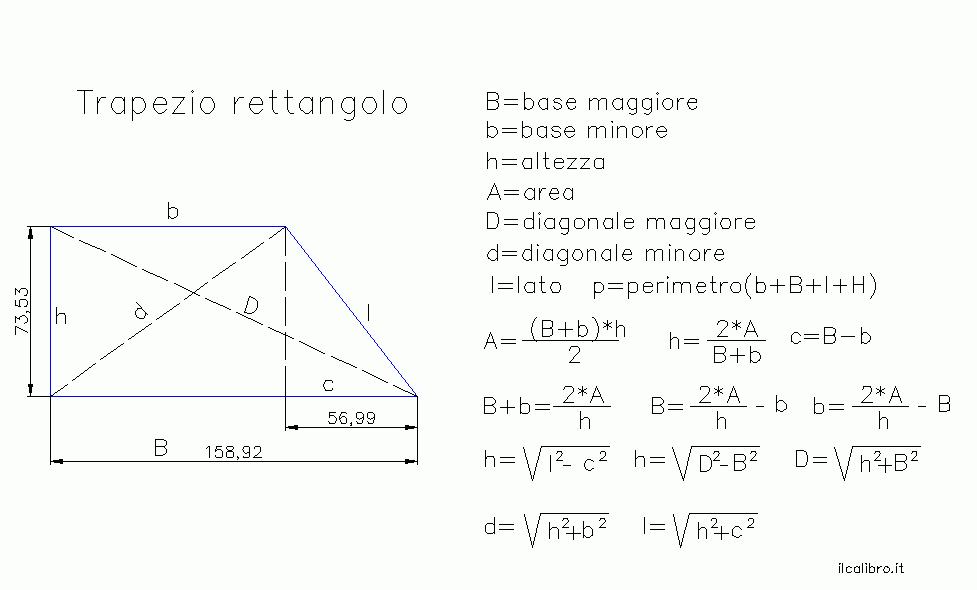Come Calcolare Il Perimetro Di Un Trapezio Rettangolo

Il trapezio rettangolo, una figura geometrica con caratteristiche ben definite, si presenta frequentemente in diversi ambiti, dalla geometria pura all'architettura. Comprenderne le proprietà, incluso come calcolare il suo perimetro, è fondamentale per risolvere problemi pratici e teorici. Questo articolo si propone di spiegare, in modo chiaro e dettagliato, come calcolare il perimetro di un trapezio rettangolo, fornendo tutti gli strumenti necessari per affrontare questa sfida.

Cos'è un Trapezio Rettangolo?

Prima di addentrarci nel calcolo del perimetro, è essenziale definire cos'è un trapezio rettangolo. Un trapezio rettangolo è un quadrilatero con le seguenti caratteristiche:

• Possiede due lati paralleli, chiamati basi (una maggiore e una minore).
• Ha due angoli retti (90 gradi) adiacenti alla stessa base. Questo significa che uno dei lati non paralleli è perpendicolare alle basi.
• Gli altri due lati non paralleli sono chiamati lati obliqui. Uno di questi è perpendicolare alle basi (e quindi coincide con l'altezza), mentre l'altro è obliquo.

Queste caratteristiche distintive rendono il trapezio rettangolo una figura geometrica particolarmente interessante e, allo stesso tempo, relativamente semplice da analizzare.

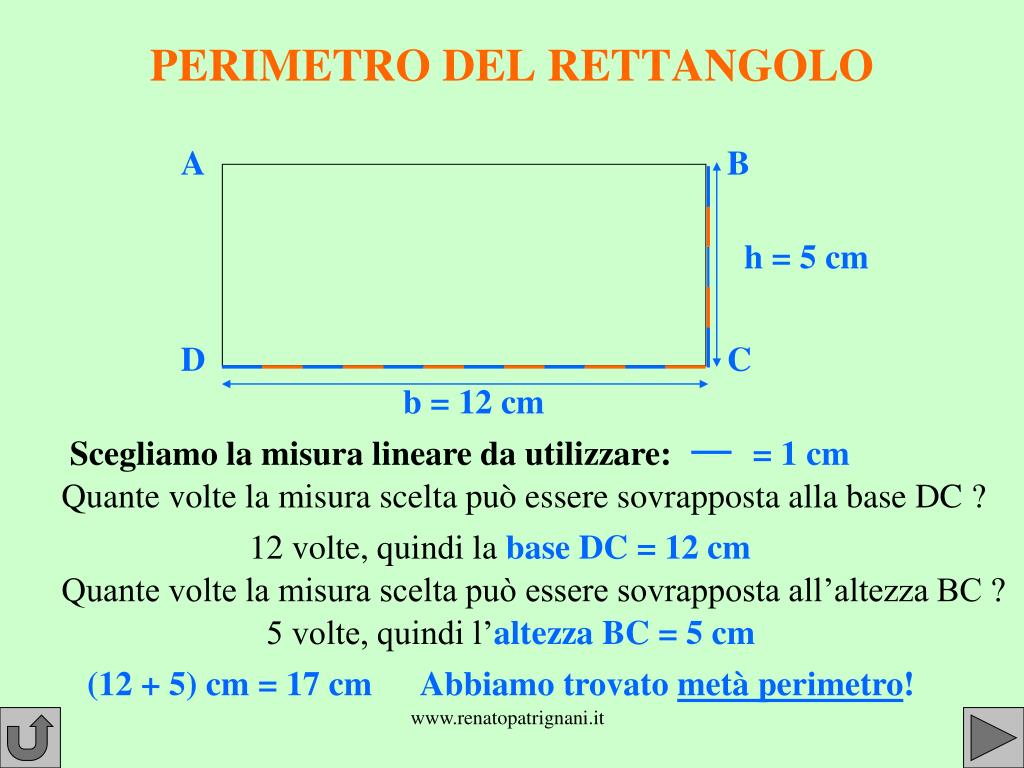
Comprendere il Perimetro

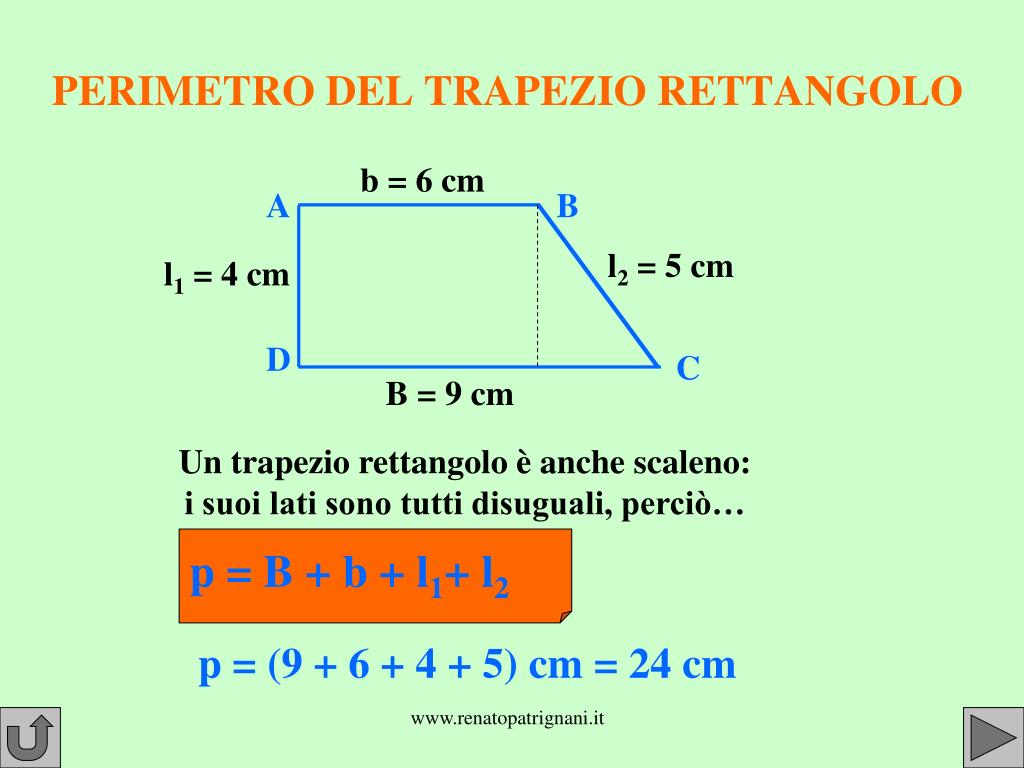
Il perimetro di qualsiasi figura geometrica bidimensionale è la somma della lunghezza di tutti i suoi lati. Nel caso del trapezio rettangolo, il perimetro è quindi dato dalla somma della base maggiore, della base minore, dell'altezza (che coincide con uno dei lati non paralleli) e del lato obliquo.

In termini matematici, possiamo scrivere:

Perimetro (P) = Base Maggiore (B) + Base Minore (b) + Altezza (h) + Lato Obliquo (l)

La sfida principale nel calcolo del perimetro di un trapezio rettangolo risiede spesso nel determinare la lunghezza del lato obliquo, che non è sempre fornita direttamente.

Come Calcolare il Lato Obliquo

Il lato obliquo può essere calcolato in diversi modi, a seconda delle informazioni disponibili. Il metodo più comune sfrutta il Teorema di Pitagora.

Applicazione del Teorema di Pitagora

Il Teorema di Pitagora afferma che in un triangolo rettangolo, il quadrato dell'ipotenusa (il lato opposto all'angolo retto) è uguale alla somma dei quadrati dei cateti (gli altri due lati).

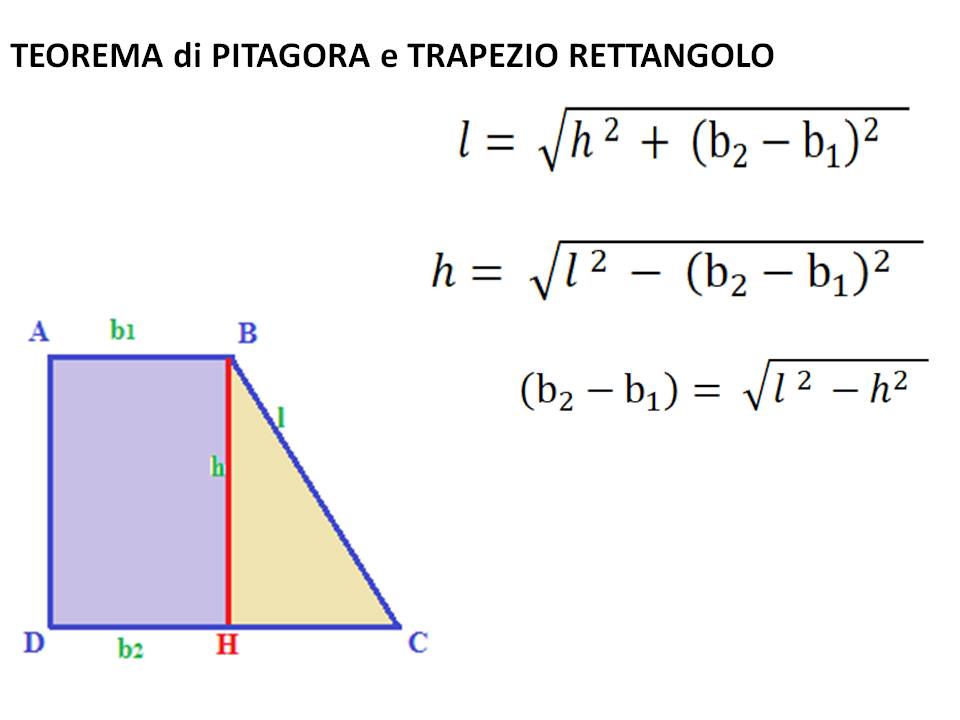
Nel nostro caso, possiamo formare un triangolo rettangolo "aggiungendo" idealmente una linea perpendicolare dalla base minore alla base maggiore. Questa linea rappresenta l'altezza del trapezio. La differenza tra la base maggiore e la base minore (B - b) costituisce uno dei cateti, l'altezza (h) è l'altro cateto, e il lato obliquo (l) è l'ipotenusa.

Quindi, applicando il Teorema di Pitagora, otteniamo:

l² = h² + (B - b)²

Per trovare la lunghezza del lato obliquo (l), basta calcolare la radice quadrata di entrambi i lati dell'equazione:

l = √(h² + (B - b)²)

Una volta calcolato il lato obliquo, possiamo facilmente calcolare il perimetro del trapezio rettangolo utilizzando la formula precedentemente illustrata.

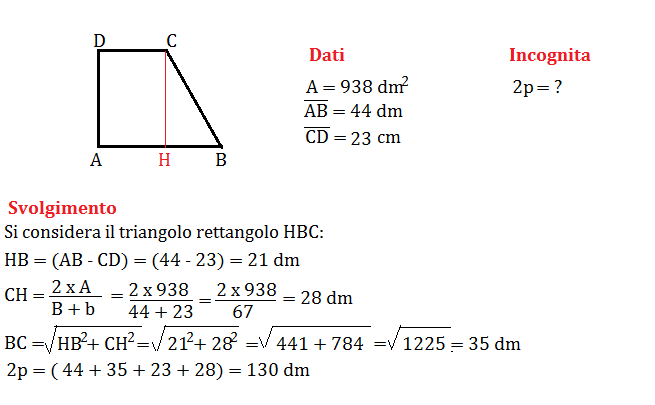
Esempio Pratico

Supponiamo di avere un trapezio rettangolo con le seguenti misure:

• Base Maggiore (B) = 10 cm
• Base Minore (b) = 6 cm
• Altezza (h) = 4 cm

Per calcolare il lato obliquo (l), applichiamo il Teorema di Pitagora:

l = √(4² + (10 - 6)²)

l = √(16 + 16)

l = √32

l ≈ 5.66 cm

Ora possiamo calcolare il perimetro:

P = 10 cm + 6 cm + 4 cm + 5.66 cm

P ≈ 25.66 cm

Pertanto, il perimetro del trapezio rettangolo è approssimativamente 25.66 cm.

Casi Particolari e Informazioni Alternative

In alcuni casi, potrebbero essere fornite informazioni diverse per calcolare il lato obliquo. Ad esempio:

• Angolo di inclinazione del lato obliquo: Se si conosce l'angolo che il lato obliquo forma con la base maggiore, si possono utilizzare le funzioni trigonometriche (seno, coseno, tangente) per calcolare la lunghezza del lato obliquo. In questo caso, la differenza tra le basi (B-b) rappresenta il cateto adiacente all'angolo, e l'altezza (h) rappresenta il cateto opposto.
• Area del trapezio: Se si conosce l'area del trapezio, si può utilizzare la formula dell'area (Area = ((B + b) * h) / 2) per ricavare l'altezza, nel caso in cui non sia fornita. Successivamente, si può procedere con il calcolo del lato obliquo tramite il Teorema di Pitagora.

È importante analizzare attentamente le informazioni fornite nel problema e scegliere il metodo più appropriato per calcolare il lato obliquo.

Applicazioni Reali

La comprensione del calcolo del perimetro del trapezio rettangolo trova applicazione in diversi contesti reali, tra cui:

• Architettura e Ingegneria: Nel progettare tetti, ponti, o altre strutture, è fondamentale calcolare con precisione le dimensioni e i perimetri delle diverse componenti, inclusi i trapezi rettangoli che possono far parte del design.
• Topografia: Nella misurazione di terreni con forme irregolari, il trapezio rettangolo può essere utilizzato per approssimare porzioni di terreno e calcolarne il perimetro, ad esempio per la recinzione.
• Design e Artigianato: Nella creazione di oggetti di design o artigianali, come cornici, mobili, o elementi decorativi, la conoscenza del perimetro del trapezio rettangolo è essenziale per garantire la corretta dimensione e proporzione degli elementi.
• Geometria Descrittiva e Disegno Tecnico: La rappresentazione e la manipolazione di figure geometriche come il trapezio rettangolo sono competenze fondamentali in queste discipline.

Conclusione

Calcolare il perimetro di un trapezio rettangolo è un'operazione relativamente semplice una volta compresi i concetti fondamentali e le proprietà di questa figura geometrica. La chiave è saper individuare le informazioni disponibili e scegliere il metodo più appropriato per calcolare la lunghezza del lato obliquo, sfruttando il Teorema di Pitagora o altre relazioni geometriche e trigonometriche.

Ricorda: La pratica rende perfetti! Esercitati con diversi esempi e problemi per consolidare la tua comprensione e acquisire maggiore sicurezza nel calcolo del perimetro del trapezio rettangolo.

Ora tocca a te! Prova a risolvere alcuni esercizi online o a creare tu stesso dei problemi. La comprensione della geometria è un tassello fondamentale per lo sviluppo del pensiero logico e della capacità di problem solving.