Come Calcolare Il Lato Obliquo Di Un Trapezio Isoscele

Il trapezio isoscele è una figura geometrica affascinante, un quadrilatero con una coppia di lati paralleli (le basi) e i due lati non paralleli (i lati obliqui) congruenti, ovvero della stessa lunghezza. Calcolare la lunghezza del lato obliquo di un trapezio isoscele è un problema comune in geometria, e la sua soluzione richiede la comprensione di alcuni concetti chiave e l'applicazione di formule specifiche. Questa guida dettagliata ti accompagnerà passo dopo passo attraverso i metodi più comuni per affrontare questo calcolo.

Comprendere il Trapezio Isoscele: Elementi Chiave

Prima di addentrarci nei calcoli, è fondamentale avere ben chiari gli elementi che definiscono un trapezio isoscele:

• Base maggiore (B): Il lato parallelo più lungo.
• Base minore (b): Il lato parallelo più corto.
• Lati obliqui (l): I due lati non paralleli, congruenti tra loro.
• Altezza (h): La distanza perpendicolare tra le due basi.

La caratteristica cruciale del trapezio isoscele è la sua simmetria rispetto all'asse perpendicolare alle basi che passa per il punto medio di entrambe. Questa simmetria semplifica notevolmente i calcoli.

Metodi per Calcolare il Lato Obliquo

Esistono diversi approcci per calcolare la lunghezza del lato obliquo di un trapezio isoscele, a seconda delle informazioni disponibili. Ecco i metodi più comuni:

1. Conoscendo l'Altezza e le Basi

Questo è il metodo più frequentemente utilizzato. Sfrutta il teorema di Pitagora e la proprietà di simmetria del trapezio isoscele. Il processo è il seguente:

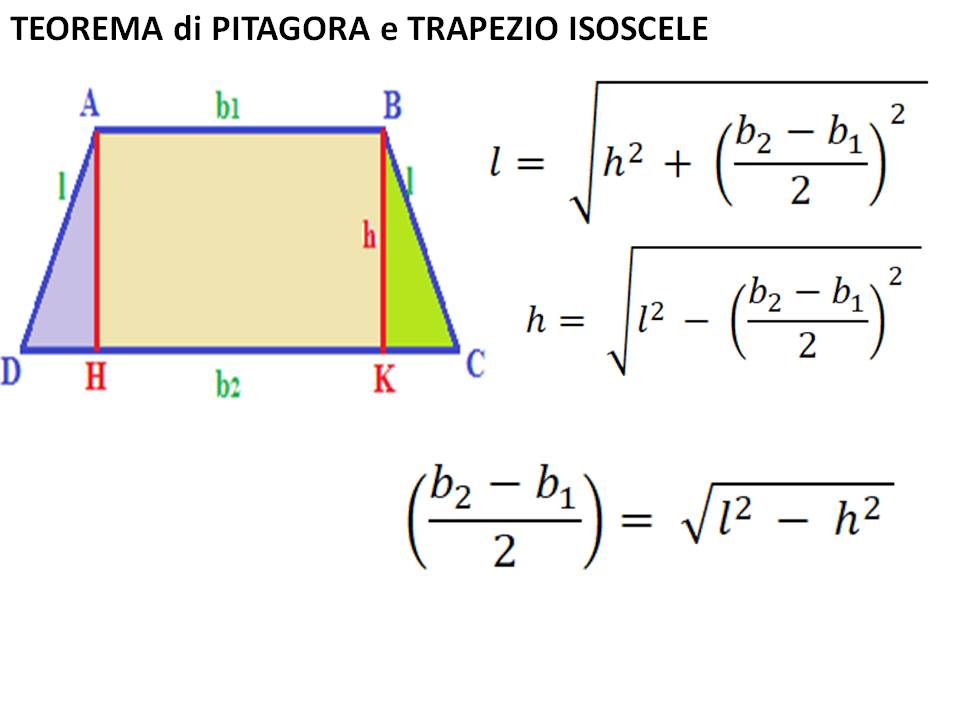
1. Calcolare la proiezione del lato obliquo sulla base maggiore: La proiezione (p) si ottiene sottraendo la base minore dalla base maggiore e dividendo il risultato per due: p = (B - b) / 2. Questa operazione è resa possibile dalla simmetria del trapezio.
2. Applicare il teorema di Pitagora: Il lato obliquo (l) è l'ipotenusa di un triangolo rettangolo avente come cateti l'altezza (h) e la proiezione (p). Pertanto: l = √(h² + p²).

Esempio: Immagina un trapezio isoscele con base maggiore di 10 cm, base minore di 6 cm e altezza di 4 cm. La proiezione del lato obliquo è (10 - 6) / 2 = 2 cm. Il lato obliquo è quindi √(4² + 2²) = √20 ≈ 4.47 cm.

2. Conoscendo l'Area, l'Altezza e le Basi

Se conosci l'area del trapezio, l'altezza e le basi, puoi calcolare indirettamente il lato obliquo, anche se questo metodo richiede un passaggio aggiuntivo. L'area del trapezio è data da: A = ((B + b) / 2) * h. Questa formula non coinvolge direttamente il lato obliquo, ma ci permette di verificarne la coerenza con gli altri dati.

Dopo aver verificato la coerenza dei dati, si procede come nel metodo precedente, calcolando la proiezione e applicando il teorema di Pitagora.

Importante: Questo metodo è utile principalmente per verificare la correttezza dei dati. Se l'area fornita non corrisponde a quella calcolata con le basi e l'altezza, significa che c'è un errore nei dati di partenza.

3. Conoscendo gli Angoli alla Base e l'Altezza

In questo caso, utilizzeremo le funzioni trigonometriche. Ricorda che gli angoli alla base (gli angoli formati dal lato obliquo con la base maggiore) sono congruenti in un trapezio isoscele.

1. Utilizzare la tangente: La tangente di uno degli angoli alla base è uguale al rapporto tra l'altezza e la proiezione del lato obliquo: tan(α) = h / p, dove α è l'angolo alla base.
2. Calcolare la proiezione: Dalla formula precedente, possiamo ricavare la proiezione: p = h / tan(α).
3. Applicare il teorema di Pitagora: Come nel primo metodo, calcoliamo il lato obliquo: l = √(h² + p²).

In alternativa, se conosci il seno o il coseno dell'angolo, puoi utilizzare le seguenti relazioni:

• sin(α) = h / l => l = h / sin(α)
• cos(α) = p / l => l = p / cos(α)

Esempio: Supponiamo che l'altezza sia di 5 cm e l'angolo alla base sia di 60 gradi. La tangente di 60 gradi è √3 ≈ 1.732. La proiezione è quindi 5 / √3 ≈ 2.89 cm. Il lato obliquo è √(5² + 2.89²) ≈ 5.77 cm. In alternativa, l = 5 / sin(60°) = 5 / (√3/2) = 10/√3 ≈ 5.77 cm.

4. Conoscendo il Perimetro e le Basi

Se conosci il perimetro (P) e le lunghezze delle basi (B e b), puoi calcolare il lato obliquo facilmente, dato che il perimetro è la somma di tutti i lati: P = B + b + 2l.

Risolvendo per l, otteniamo: l = (P - B - b) / 2.

Esempio: Se il perimetro è 30 cm, la base maggiore è 10 cm e la base minore è 6 cm, il lato obliquo è (30 - 10 - 6) / 2 = 7 cm.

Esempio Pratico: Un Tetto a Forma di Trapezio

Immagina di dover calcolare la quantità di materiale necessario per rivestire una porzione di tetto a forma di trapezio isoscele. La base inferiore del tetto (la base maggiore del trapezio) è di 8 metri, la base superiore (la base minore) è di 5 metri, e l'altezza del tetto è di 3 metri. Dobbiamo calcolare la lunghezza dei lati obliqui per determinare l'area totale da rivestire.

Utilizziamo il primo metodo: calcoliamo la proiezione del lato obliquo: (8 - 5) / 2 = 1.5 metri. Applichiamo il teorema di Pitagora: √(3² + 1.5²) = √11.25 ≈ 3.35 metri. Quindi, ogni lato obliquo misura circa 3.35 metri.

Ora, possiamo calcolare l'area del trapezio: ((8 + 5) / 2) * 3 = 19.5 metri quadrati. Dovremmo considerare un extra per sovrapposizioni e tagli, quindi è consigliabile ordinare almeno 21 metri quadrati di materiale.

Consigli e Precauzioni

• Verifica i dati: Assicurati che i dati forniti siano coerenti e privi di errori. Ad esempio, la somma delle lunghezze delle basi deve essere inferiore al perimetro.
• Unità di misura: Utilizza sempre la stessa unità di misura per tutte le lunghezze.
• Approssimazioni: Se utilizzi la calcolatrice per calcolare radici quadrate o funzioni trigonometriche, presta attenzione alle approssimazioni. Arrotonda solo alla fine del calcolo per evitare errori cumulativi.
• Disegno: Disegna sempre un diagramma del trapezio per visualizzare meglio il problema e identificare le relazioni tra i lati e gli angoli.

Conclusioni

Calcolare il lato obliquo di un trapezio isoscele è un problema geometrico che può essere risolto utilizzando diversi approcci, a seconda delle informazioni disponibili. La chiave per il successo è comprendere le proprietà del trapezio isoscele, in particolare la sua simmetria, e applicare correttamente il teorema di Pitagora e le funzioni trigonometriche. Ricorda di verificare sempre i dati e di utilizzare un diagramma per visualizzare il problema.

Sperimenta con diversi esercizi e problemi per consolidare la tua comprensione. La geometria è una disciplina che si impara con la pratica!