Come Calcolare I Cateti Di Un Triangolo Rettangolo Conoscendo L'ipotenusa
Se ti trovi di fronte a un problema di geometria che ti chiede di calcolare i cateti di un triangolo rettangolo, conoscendo solamente l'ipotenusa, non disperare! Molti studenti si sentono persi in queste situazioni, soprattutto perché sembra che manchino informazioni cruciali. Ma con gli strumenti giusti e un po' di logica, la soluzione è a portata di mano. Capisco perfettamente la frustrazione di sentirsi bloccati, soprattutto quando si tratta di matematica. L'obiettivo di questo articolo è proprio quello di guidarti passo passo, rendendo il processo il più chiaro e semplice possibile.
Perché è importante saper calcolare i cateti?
La geometria, e in particolare i triangoli rettangoli, non sono solo un esercizio teorico. Hanno applicazioni pratiche in molti campi, dalla costruzione all'ingegneria, dalla navigazione all'arte. Pensa ad esempio a un architetto che deve progettare una rampa, o a un ingegnere che deve calcolare la forza esercitata su un elemento strutturale. In tutti questi casi, la conoscenza delle relazioni tra i lati di un triangolo rettangolo può essere fondamentale. Saper risolvere questi problemi non solo ti aiuta a superare gli esami, ma ti fornisce anche competenze utili nella vita reale.
Il problema: Cosa ci manca?
Normalmente, per risolvere un triangolo rettangolo, abbiamo bisogno di conoscere almeno due lati, o un lato e un angolo acuto. Conoscendo solo l'ipotenusa, ci manca un'informazione cruciale: la lunghezza di uno dei cateti o, in alternativa, l'ampiezza di uno degli angoli acuti. Questo significa che dobbiamo trovare un modo per "creare" questa informazione mancante.
Metodi per Calcolare i Cateti
Esistono diversi approcci per risolvere questo problema. La scelta del metodo dipende spesso dalle informazioni aggiuntive che potresti avere o dalla specifica formulazione del problema. Esploreremo i metodi più comuni, cercando di capire i loro punti di forza e le loro limitazioni.
1. Conoscere un Angolo Acuto
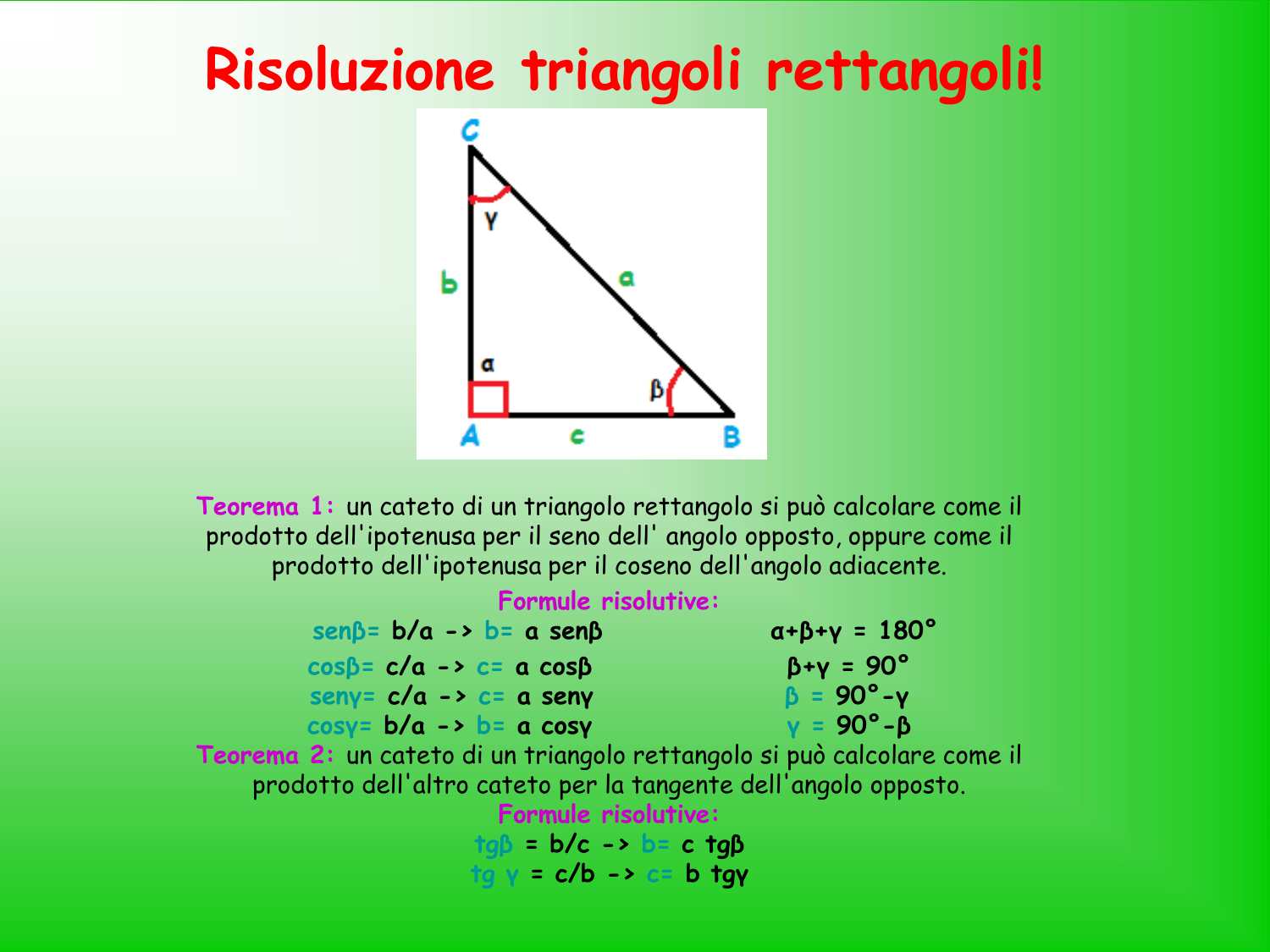
Questo è lo scenario più semplice. Se conosci l'ampiezza di uno degli angoli acuti (diverso da 90°), puoi utilizzare le funzioni trigonometriche seno e coseno.
Ricorda le definizioni:
- Seno (sin): cateto opposto / ipotenusa
- Coseno (cos): cateto adiacente / ipotenusa
Quindi:
- Se conosci l'angolo α, il cateto opposto ad α è: cateto_opposto = ipotenusa * sin(α)
- Se conosci l'angolo α, il cateto adiacente ad α è: cateto_adiacente = ipotenusa * cos(α)
Esempio:
Ipotenusa = 10 cm, Angolo α = 30°
- Cateto opposto = 10 cm * sin(30°) = 10 cm * 0.5 = 5 cm
- Cateto adiacente = 10 cm * cos(30°) = 10 cm * 0.866 = 8.66 cm (circa)
2. Conoscere un'Altra Relazione tra i Cateti
A volte, il problema può darti un'informazione indiretta sulla relazione tra i cateti. Ad esempio, potresti sapere che un cateto è il doppio dell'altro, oppure che la loro somma è un certo valore.
Esempio 1: Un cateto è il doppio dell'altro
Ipotenusa = 5, Cateto A = 2 * Cateto B
Usiamo il Teorema di Pitagora: A² + B² = ipotenusa²
Sostituiamo A con 2B: (2B)² + B² = 5²
4B² + B² = 25
5B² = 25
B² = 5
B = √5
A = 2 * √5
Esempio 2: La somma dei cateti è un certo valore
Ipotenusa = 13, A + B = 17
In questo caso, possiamo esprimere un cateto in funzione dell'altro: A = 17 - B
Sostituiamo nel Teorema di Pitagora: (17 - B)² + B² = 13²
289 - 34B + B² + B² = 169
2B² - 34B + 120 = 0
B² - 17B + 60 = 0
Risolviamo l'equazione di secondo grado per trovare i valori possibili di B. Poi, calcoliamo A usando A = 17 - B.
Ricorda che un'equazione di secondo grado può avere due soluzioni, una soluzione o nessuna soluzione. Dobbiamo controllare se le soluzioni ottenute sono fisicamente accettabili (cioè, se sono numeri positivi e se la loro somma è uguale al valore dato).
3. Triangoli Rettangoli Speciali
Esistono alcuni triangoli rettangoli con rapporti specifici tra i lati che sono utili da memorizzare:
- Triangolo 30-60-90: I lati sono in rapporto 1 : √3 : 2 (il lato più corto è metà dell'ipotenusa, il lato intermedio è √3 volte il lato più corto).
- Triangolo 45-45-90: È un triangolo rettangolo isoscele. I cateti sono uguali e l'ipotenusa è √2 volte la lunghezza di un cateto.
Se il tuo triangolo rientra in una di queste categorie, puoi calcolare i cateti molto rapidamente.
Esempio: Triangolo 45-45-90, ipotenusa = 7
Cateto = ipotenusa / √2 = 7 / √2 = (7√2) / 2
4. Proiezioni dei Cateti sull'Ipotenusa (Teoremi di Euclide)
I Teoremi di Euclide stabiliscono delle relazioni tra i cateti, l'ipotenusa e le proiezioni dei cateti sull'ipotenusa.
- Primo Teorema di Euclide: In un triangolo rettangolo, il quadrato costruito su un cateto è equivalente al rettangolo che ha per lati l'ipotenusa e la proiezione del cateto stesso sull'ipotenusa.
- Secondo Teorema di Euclide: In un triangolo rettangolo, il quadrato costruito sull'altezza relativa all'ipotenusa è equivalente al rettangolo che ha per lati le proiezioni dei cateti sull'ipotenusa.
Anche se questi teoremi possono sembrare complicati, in realtà possono essere utili se conosci la proiezione di uno dei cateti sull'ipotenusa.
Esempio: Ipotenusa = 25, Proiezione del cateto A sull'ipotenusa = 9
Usiamo il Primo Teorema di Euclide: A² = ipotenusa * proiezione
A² = 25 * 9
A² = 225
A = 15
Ora possiamo usare il Teorema di Pitagora per trovare B: B² = ipotenusa² - A² = 25² - 15² = 625 - 225 = 400
B = 20
Cosa fare se il problema sembra impossibile?
A volte, i problemi di geometria possono sembrare appositamente progettati per confonderti. Ecco alcuni suggerimenti:
- Disegna un diagramma: Un disegno chiaro e preciso può aiutarti a visualizzare il problema e a identificare le relazioni tra i lati e gli angoli.
- Scrivi tutte le informazioni che hai: Anche se alcune informazioni sembrano irrilevanti, potrebbero esserti utili in seguito.
- Cerca triangoli simili: Se ci sono altri triangoli nel diagramma, potrebbero essere simili al triangolo rettangolo che stai cercando di risolvere. I triangoli simili hanno angoli uguali e lati proporzionali.
- Usa la tua intuizione: Non aver paura di sperimentare diverse strategie. A volte, la soluzione arriva quando meno te lo aspetti.
- Chiedi aiuto: Se sei bloccato, non esitare a chiedere aiuto a un insegnante, a un tutor o a un compagno di classe.
Un consiglio importante
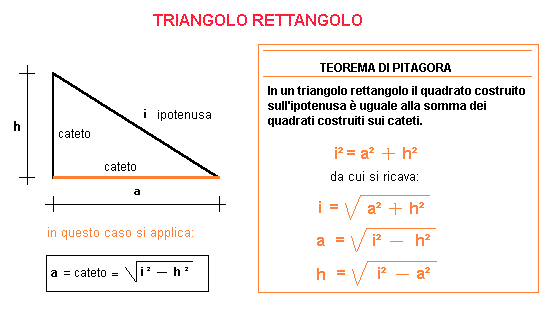
Ricorda sempre il Teorema di Pitagora: A² + B² = C², dove A e B sono i cateti e C è l'ipotenusa. Questo teorema è la pietra angolare della geometria del triangolo rettangolo e può esserti utile in molte situazioni.
Affrontare le Obiezioni: "È solo teoria!"
Alcuni potrebbero pensare che la trigonometria e la geometria siano solo esercizi teorici senza alcuna utilità pratica. Non è affatto vero! Come accennato all'inizio, queste conoscenze sono fondamentali in molti campi professionali e nella vita quotidiana. Dalla semplice costruzione di una libreria al calcolo della distanza da un punto all'altro usando un GPS, i principi geometrici sono costantemente applicati.
Ricorda: La pratica rende perfetti!
Più esercizi fai, più facile diventerà risolvere i problemi di geometria. Non scoraggiarti se all'inizio trovi difficoltà. Con la pratica, svilupperai una maggiore comprensione dei concetti e una maggiore sicurezza nelle tue capacità.
Spero che questa guida ti sia stata utile. Ora, prova a mettere in pratica quello che hai imparato risolvendo alcuni esercizi. Qual è il prossimo problema di geometria che affronterai?