Colori Dei Regoli Da 1 A 10

Ciao! Ti sei mai chiesto cosa si nasconde dietro i colori dei regoli? Magari li hai visti a scuola, usati dai tuoi figli o nipoti, e ti sei chiesto perché ognuno ha un colore specifico. Non sono semplici bastoncini colorati, ma potenti strumenti che aiutano a comprendere la matematica in modo visuale e intuitivo. Molti bambini (e anche adulti!) faticano con i concetti astratti come numeri e operazioni. I regoli di Cuisenaire, con i loro colori distinti, offrono un ponte tangibile tra l'idea e la realtà.

Perché Usare i Regoli di Cuisenaire?

Prima di addentrarci nei colori specifici, cerchiamo di capire perché questi strumenti sono così efficaci. Molti metodi tradizionali di insegnamento della matematica si concentrano sull'apprendimento a memoria e sull'esecuzione di algoritmi, spesso senza una vera comprensione del "perché" dietro le operazioni. I regoli offrono un'alternativa più coinvolgente e profonda:

Visualizzazione Concreta: Trasformano concetti astratti in qualcosa di visibile e manipolabile.
Apprendimento Attivo: Incoraggiano gli studenti a esplorare e sperimentare, scoprendo le relazioni matematiche da soli.
Comprensione Profonda: Aiutano a costruire una solida base per concetti matematici più avanzati.

Immagina di dover spiegare a un bambino la frazione 1/2. Potresti disegnarla su una lavagna, ma sarebbe molto più efficace mostrare un regolo arancione (che rappresenta il 10) e confrontarlo con un regolo giallo (che rappresenta il 5). Il bambino vedrebbe immediatamente che il regolo giallo è esattamente la metà del regolo arancione. Questa esperienza diretta rende il concetto molto più memorabile e significativo.

I Colori dei Regoli: Un Sistema Ragionato

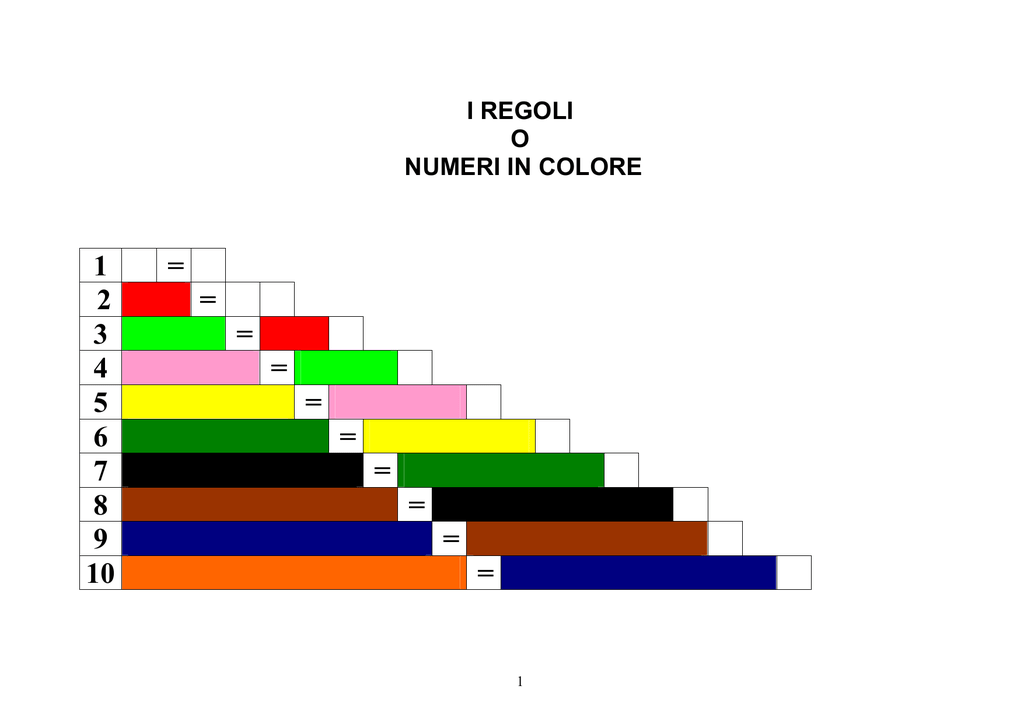
Ogni regolo di Cuisenaire ha una lunghezza specifica, che corrisponde a un numero da 1 a 10, e un colore ben preciso. Questi colori non sono scelti a caso, ma seguono un sistema logico che aiuta a memorizzare le relazioni tra i numeri. Ecco una panoramica:

La Scala Cromatica e le Famiglie di Colori

I regoli sono organizzati in "famiglie" di colori, basate sulle loro relazioni numeriche. Questa organizzazione non è casuale e aiuta la memorizzazione e la comprensione delle relazioni tra i numeri.

Bianco (1): È l'unità di misura, il punto di partenza.
Rosso (2): È il primo numero pari e rappresenta la base della "famiglia" dei pari.
Verde Chiaro (3): Inizia la "famiglia" dei multipli di 3.
Rosa (4): Appartiene alla famiglia del rosso (2x2).
Giallo (5): Rappresenta la metà di 10 ed è un punto di riferimento importante.
Verde Scuro (6): È un multiplo sia di 2 che di 3, quindi appartiene ad entrambe le famiglie.
Nero (7): È un numero primo e non ha relazioni semplici con gli altri.
Marrone (8): Appartiene alla famiglia del rosso (2x2x2).
Blu (9): Appartiene alla famiglia del verde chiaro (3x3).
Arancione (10): Rappresenta la base del sistema decimale.

Come puoi vedere, i colori non sono casuali. I multipli di un numero tendono ad avere colori simili. Ad esempio, il rosa (4) e il marrone (8) sono entrambi tonalità derivate dal rosso, proprio come il 4 e l'8 sono multipli di 2. Questo sistema cromatico aiuta a rafforzare la comprensione delle relazioni numeriche.

Descrizione Dettagliata dei Colori e del Loro Significato

Regolo Bianco (1): Il più piccolo, rappresenta l'unità. È il mattone fondamentale con cui si costruiscono tutti gli altri numeri. Viene spesso utilizzato per misurare gli altri regoli e per comprendere concetti come la scomposizione dei numeri.
Regolo Rosso (2): Il doppio dell'unità. Introduce il concetto di "paio" e viene utilizzato per esplorare la divisibilità per 2.
Regolo Verde Chiaro (3): Introduce la "terna" e il concetto di multiplo. È utile per iniziare a lavorare con le tabelline del 3.
Regolo Rosa (4): Il doppio del rosso (2x2). Mostra come si possono combinare numeri per crearne altri più grandi.
Regolo Giallo (5): Rappresenta la metà del regolo arancione (10). È un punto di riferimento importante per comprendere le frazioni e le percentuali.
Regolo Verde Scuro (6): Unisce le caratteristiche del regolo rosso (2) e del regolo verde chiaro (3). Aiuta a comprendere i concetti di minimo comune multiplo e massimo comun divisore.
Regolo Nero (7): Un numero primo, difficile da scomporre. Introduce l'idea che non tutti i numeri sono facilmente divisibili.
Regolo Marrone (8): Il doppio del rosa (4) e il quadruplo del rosso (2). Rafforza la comprensione delle potenze del 2.
Regolo Blu (9): Il triplo del verde chiaro (3). Introduce il concetto di quadrato (3x3).
Regolo Arancione (10): La base del nostro sistema numerico. Rappresenta la "decina" e viene utilizzato per lavorare con i numeri a due cifre.

Ad esempio, per spiegare l'addizione 3 + 2, si può affiancare il regolo verde chiaro (3) al regolo rosso (2) e poi cercare un unico regolo che abbia la stessa lunghezza. Si troverà il regolo giallo (5), dimostrando visivamente che 3 + 2 = 5.

Contrarietà e Critiche: I Regoli Funzionano Davvero?

Nonostante i numerosi vantaggi, alcuni educatori esprimono riserve sull'uso esclusivo dei regoli. Alcuni sostengono che potrebbero diventare una "stampella" e impedire agli studenti di sviluppare competenze di calcolo mentale e astratto. Altri ritengono che richiedano troppo tempo per essere implementati in classe. È importante sottolineare che i regoli non sono una panacea e dovrebbero essere utilizzati come uno strumento tra tanti, integrati con altri metodi di insegnamento. L'obiettivo finale è aiutare gli studenti a interiorizzare i concetti matematici e a sviluppare la capacità di risolvere problemi in modo autonomo, non a dipendere esclusivamente dai regoli.

Inoltre, è cruciale che gli insegnanti siano adeguatamente formati sull'uso efficace dei regoli, altrimenti il loro potenziale potrebbe non essere sfruttato appieno. Un uso improprio potrebbe, infatti, confondere gli studenti anziché aiutarli.

Soluzioni e Strategie Pratiche

Come possiamo superare queste critiche e massimizzare i benefici dei regoli? Ecco alcune strategie:

Integrazione con Altri Metodi: Utilizzare i regoli come punto di partenza per poi introdurre gradualmente metodi più astratti.
Variazione delle Attività: Proporre attività diverse che stimolino la creatività e il pensiero critico.
Formazione degli Insegnanti: Assicurarsi che gli insegnanti abbiano una solida comprensione dei principi matematici sottostanti e delle tecniche di insegnamento efficaci.
Valutazione Continua: Monitorare i progressi degli studenti e adattare l'approccio di conseguenza.

Ad esempio, dopo aver utilizzato i regoli per introdurre il concetto di frazione, si può passare a utilizzare rappresentazioni grafiche e poi a risolvere problemi più complessi con carta e penna. L'importante è costruire una transizione graduale dal concreto all'astratto.

L'Impatto Reale: Storie di Successo

Molti insegnanti hanno testimoniato l'impatto positivo dei regoli sui loro studenti. Bambini che prima faticavano con la matematica, improvvisamente iniziano a comprendere i concetti e a mostrare entusiasmo. I regoli rendono l'apprendimento più accessibile e divertente, soprattutto per gli studenti con difficoltà di apprendimento o con stili di apprendimento visivi e cinestetici.

Ho sentito di una bambina che non riusciva a capire il concetto di divisione. Dopo aver iniziato a usare i regoli, è stata in grado di visualizzare il processo di divisione come una sorta di "suddivisione" dei regoli in gruppi uguali. Questo le ha permesso di superare le sue difficoltà e di sviluppare una maggiore fiducia nelle sue capacità matematiche.

Conclusione: Un Invito all'Azione

I regoli di Cuisenaire sono molto più che semplici giocattoli colorati. Sono potenti strumenti che possono trasformare il modo in cui i bambini imparano la matematica. Offrono un approccio concreto, visivo e coinvolgente che può aiutare a superare le difficoltà e a costruire una solida base per il futuro. Nonostante alcune critiche, i benefici dei regoli sono innegabili, soprattutto se utilizzati in modo efficace e integrati con altri metodi di insegnamento.

Ora ti invito a riflettere: come potresti utilizzare i regoli per aiutare i tuoi figli, nipoti o studenti a comprendere meglio la matematica? Hai mai provato a usarli tu stesso per visualizzare un concetto matematico che ti sembrava difficile? Prova, sperimenta e scopri il potere dei regoli!