Colore Dei Regoli Da 1 A 10

Capita spesso, soprattutto a chi si avvicina al mondo della matematica e dell'insegnamento ai bambini, di sentir parlare dei Regoli di Cuisenaire. Ma di cosa si tratta esattamente? E perché i loro colori sono così importanti? Comprendere l'importanza del colore dei regoli da 1 a 10 è fondamentale per sbloccare il loro pieno potenziale didattico. Molti genitori e insegnanti si trovano di fronte alla sfida di rendere la matematica più accessibile e concreta per i bambini, e i regoli di Cuisenaire rappresentano un'ottima soluzione.

Cosa sono i Regoli di Cuisenaire?

I Regoli di Cuisenaire sono un materiale didattico composto da barrette di legno colorate di lunghezza variabile. Ogni lunghezza corrisponde a un numero da 1 a 10. L'inventore di questo strumento, Georges Cuisenaire, era un insegnante belga che si accorse di come i bambini potessero comprendere meglio i concetti matematici astratti manipolando oggetti concreti.

Come funzionano?

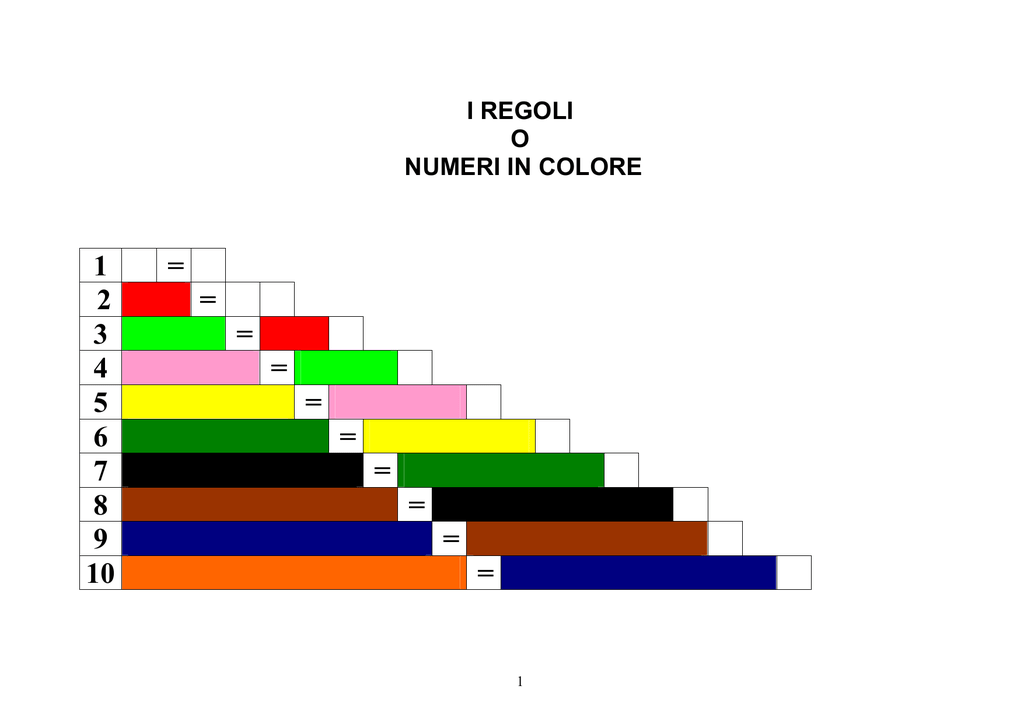
Ogni colore rappresenta una lunghezza specifica, e quindi un numero:

Bianco (1): Il regolo più piccolo, rappresenta l'unità.
Rosso (2): Lungo il doppio del bianco.
Verde chiaro (3): Lungo il triplo del bianco.
Rosa (4): Lungo quattro volte il bianco.
Giallo (5): Lungo cinque volte il bianco.
Verde scuro (6): Lungo sei volte il bianco.
Nero (7): Lungo sette volte il bianco.
Marrone (8): Lungo otto volte il bianco.
Blu (9): Lungo nove volte il bianco.
Arancione (10): Il regolo più lungo, lungo dieci volte il bianco.

L'uso dei regoli permette ai bambini di visualizzare e manipolare concretamente le relazioni tra i numeri, facilitando la comprensione delle operazioni aritmetiche di base (addizione, sottrazione, moltiplicazione, divisione) e concetti più avanzati come le frazioni e l'algebra.

L'importanza dei Colori

I colori non sono scelti a caso. Dietro la loro selezione c'è una logica precisa, pensata per facilitare la memorizzazione e l'uso dei regoli. Non si tratta solo di estetica, ma di una strategia didattica accuratamente studiata.

La relazione tra i colori e le lunghezze dei regoli permette ai bambini di:

Associare facilmente il colore al numero: Questo rende l'apprendimento più intuitivo e meno mnemonico.
Visualizzare le relazioni tra i numeri: Ad esempio, combinando un regolo rosso (2) e un regolo verde chiaro (3) si ottiene un regolo giallo (5).
Sviluppare il pensiero logico-matematico: Attraverso la manipolazione e la sperimentazione con i regoli, i bambini imparano a risolvere problemi e a ragionare in modo astratto.

I colori, quindi, non sono solo decorativi, ma parte integrante del metodo. Aiutano i bambini a costruire un ponte tra il mondo concreto e il mondo astratto dei numeri.

Esempi di Utilizzo

Vediamo alcuni esempi pratici di come i regoli di Cuisenaire possono essere utilizzati per insegnare diversi concetti matematici:

Addizione: Per sommare 2 + 3, si prendono un regolo rosso (2) e un regolo verde chiaro (3). Si affiancano i due regoli e si cerca il regolo che ha la stessa lunghezza della combinazione. In questo caso, è il regolo giallo (5).
Sottrazione: Per sottrarre 5 - 2, si prende un regolo giallo (5) e si sovrappone un regolo rosso (2). La parte del regolo giallo che rimane scoperta corrisponde al regolo verde chiaro (3).
Moltiplicazione: Per moltiplicare 2 x 3, si prendono tre regoli rossi (2) e si affiancano. La lunghezza totale corrisponde a un regolo verde scuro (6).
Divisione: Per dividere 6 : 2, si prende un regolo verde scuro (6) e si cerca quanti regoli rossi (2) sono necessari per coprirlo completamente. In questo caso, sono necessari tre regoli rossi.
Frazioni: Per rappresentare 1/2, si prende un regolo rosso (2) e un regolo bianco (1). Il regolo bianco rappresenta la metà del regolo rosso.

Questi sono solo alcuni esempi. Le possibilità di utilizzo dei regoli sono molteplici e dipendono dalla creatività dell'insegnante e dalle esigenze degli studenti.

Affrontare le Critiche

Alcuni potrebbero obiettare che l'utilizzo dei regoli di Cuisenaire potrebbe rendere i bambini troppo dipendenti dal materiale concreto e ostacolare lo sviluppo del pensiero astratto. È una critica valida, ma è importante ricordare che i regoli sono un strumento di transizione. Il loro scopo è quello di aiutare i bambini a comprendere i concetti matematici in modo intuitivo e graduale. Una volta che i concetti sono stati interiorizzati, è importante incoraggiare i bambini a utilizzare strategie di calcolo più astratte.

Un altro punto di discussione potrebbe riguardare il costo dei regoli. Esistono alternative più economiche, come i regoli fatti in casa con cartoncino colorato. Tuttavia, i regoli di legno offrono una maggiore durata e resistenza, e la loro forma precisa facilita la manipolazione. L'investimento, quindi, può essere giustificato, soprattutto se i regoli vengono utilizzati in classe o da più bambini.

Soluzioni e Suggerimenti

Per sfruttare al meglio il potenziale dei regoli di Cuisenaire, ecco alcuni suggerimenti:

Iniziare con attività semplici: Presentare i regoli ai bambini gradualmente, iniziando con attività di esplorazione libera e di riconoscimento dei colori e delle lunghezze.
Utilizzare giochi e attività interattive: Rendere l'apprendimento divertente e coinvolgente attraverso giochi di costruzione, indovinelli matematici e sfide a squadre.
Collegare i regoli alla vita reale: Utilizzare i regoli per risolvere problemi pratici che si presentano nella vita di tutti i giorni, come misurare oggetti, dividere cibo o calcolare sconti.
Incoraggiare la creatività: Invitare i bambini a creare le proprie figure e i propri schemi con i regoli, stimolando la loro immaginazione e il loro pensiero divergente.
Adattare le attività alle esigenze individuali: Tenere conto dei diversi stili di apprendimento e dei ritmi di sviluppo di ciascun bambino.

È fondamentale che l'insegnante o il genitore assuma un ruolo di facilitatore, guidando i bambini nella scoperta e nell'esplorazione dei concetti matematici, senza fornire soluzioni predefinite.

Oltre la Matematica

Sebbene siano principalmente utilizzati per l'apprendimento della matematica, i regoli di Cuisenaire possono essere impiegati anche in altri ambiti, come:

Sviluppo delle capacità motorie: La manipolazione dei regoli aiuta a sviluppare la coordinazione occhio-mano e la motricità fine.
Sviluppo del linguaggio: I regoli possono essere utilizzati per descrivere forme, colori e relazioni spaziali, ampliando il vocabolario dei bambini.
Sviluppo della creatività: La possibilità di creare figure e schemi con i regoli stimola l'immaginazione e la capacità di problem solving.
Apprendimento delle lingue straniere: I colori dei regoli possono essere utilizzati per insegnare i nomi dei colori in altre lingue.

I regoli di Cuisenaire, quindi, non sono solo uno strumento per imparare la matematica, ma un vero e proprio strumento educativo a 360 gradi.

In definitiva, il colore dei regoli da 1 a 10 non è un dettaglio trascurabile, ma un elemento cruciale per facilitare l'apprendimento della matematica e lo sviluppo di diverse abilità nei bambini. L'uso consapevole e creativo di questo strumento può fare la differenza nel rendere la matematica più accessibile, divertente e significativa.

Dopo aver letto questo articolo, vi sentite ispirati a provare i Regoli di Cuisenaire con i vostri bambini o studenti? Quale attività vi piacerebbe sperimentare per prima?