Circonferenza Inscritta In Un Triangolo Rettangolo

La circonferenza inscritta in un triangolo rettangolo rappresenta un concetto geometrico affascinante e con implicazioni pratiche in diversi campi. Esploreremo in dettaglio questa relazione, analizzando le sue proprietà, le formule coinvolte e le sue applicazioni.
Proprietà Fondamentali della Circonferenza Inscritta
Una circonferenza inscritta in un triangolo è una circonferenza che è tangente a tutti e tre i lati del triangolo. Il centro di questa circonferenza è chiamato incentro, e si trova all'intersezione delle bisettrici degli angoli interni del triangolo. Questa proprietà è cruciale perché determina univocamente la posizione della circonferenza all'interno del triangolo.
Incentro e Bisettrici
L'incentro è il punto di incontro delle tre bisettrici interne del triangolo. Una bisettrice è una retta che divide un angolo in due angoli congruenti. Poiché l'incentro è equidistante da tutti i lati del triangolo (essendo il centro della circonferenza tangente), questo punto rappresenta il centro ideale per la circonferenza inscritta. Per trovare l'incentro, è sufficiente tracciare due bisettrici qualsiasi; la loro intersezione determina la posizione dell'incentro.
Raggio della Circonferenza Inscritta
Il raggio della circonferenza inscritta, spesso indicato con la lettera r, è la distanza dall'incentro a ciascuno dei lati del triangolo. Questo raggio è perpendicolare al lato nel punto di tangenza. Il raggio della circonferenza inscritta in un triangolo rettangolo può essere calcolato con formule specifiche, rendendo più semplice la sua determinazione.
Calcolo del Raggio nel Triangolo Rettangolo
Nel caso di un triangolo rettangolo, il calcolo del raggio della circonferenza inscritta si semplifica notevolmente. Siano a e b le lunghezze dei cateti e c la lunghezza dell'ipotenusa del triangolo rettangolo. Esistono diverse formule per calcolare il raggio r. Una delle più comuni è:
r = (a + b - c) / 2
Questa formula deriva dalle proprietà geometriche del triangolo rettangolo e della circonferenza inscritta. Un'altra formula equivalente, che spesso risulta più utile in contesti specifici, è:
r = A / s
dove A è l'area del triangolo e s è il semiperimetro, calcolato come s = (a + b + c) / 2. Questa formula generale si applica a qualsiasi triangolo, non solo a quelli rettangoli, ma è particolarmente utile nel contesto specifico.
Dimostrazione della Formula
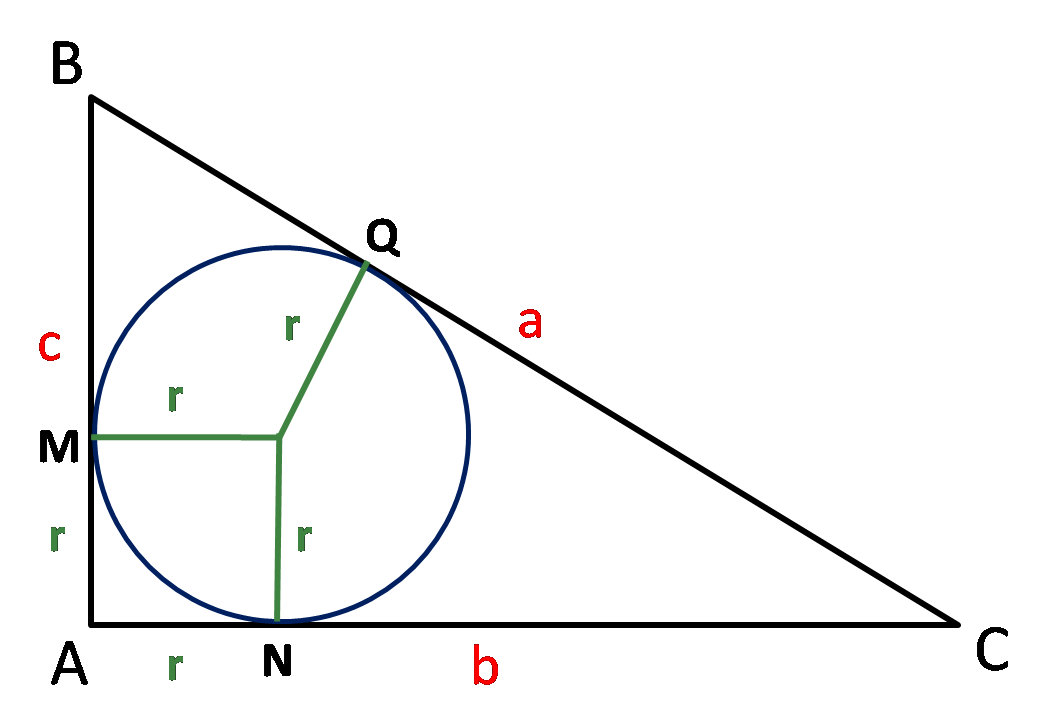
La formula r = (a + b - c) / 2 può essere dimostrata considerando le tangenti alla circonferenza inscritta dai vertici del triangolo. Sia I l'incentro del triangolo rettangolo ABC, con angolo retto in C. Siano D, E, ed F i punti di tangenza della circonferenza inscritta sui lati BC, AC, e AB rispettivamente. Allora, ID, IE, ed IF sono raggi della circonferenza e sono perpendicolari ai rispettivi lati. Ne consegue che CDIE è un quadrato di lato r. Quindi, CD = CE = r. Inoltre, AD = AE, BD = BF, e CF = CE. Allora a = BD + r e b = AE + r. Quindi, AD = b - r e BD = a - r. Poiché AB = c = AD + BD, si ha c = (b - r) + (a - r), da cui c = a + b - 2r, e infine r = (a + b - c) / 2.
Applicazioni Pratiche e Real-World
La circonferenza inscritta in un triangolo rettangolo, e la sua relazione con i lati del triangolo, non è solo un esercizio teorico di geometria. Trova applicazioni concrete in vari ambiti, dall'architettura all'ingegneria, passando per la computer grafica.
Architettura e Ingegneria
In architettura, la conoscenza delle proprietà della circonferenza inscritta può essere utile per la progettazione di spazi che richiedono simmetria e armonia visiva. Ad esempio, nella progettazione di giardini o cortili con forme triangolari, il posizionamento di una fontana circolare all'interno del triangolo, calcolata come circonferenza inscritta, può creare un punto focale esteticamente gradevole.
In ingegneria, queste conoscenze possono essere applicate nella progettazione di strutture triangolari, come ponti o capriate, dove la circonferenza inscritta può rappresentare un'area di rinforzo o un punto di ancoraggio. La precisione nel calcolo del raggio e del centro è fondamentale per garantire la stabilità e la sicurezza della struttura.
Computer Grafica e Modellazione 3D
Nel campo della computer grafica e della modellazione 3D, la circonferenza inscritta può essere utilizzata per creare texture e pattern geometrici su superfici triangolari. Algoritmi che sfruttano le proprietà della circonferenza inscritta possono essere impiegati per generare automaticamente layout complessi e dettagliati. Inoltre, la circonferenza inscritta può essere utilizzata per ottimizzare la triangolazione di superfici, riducendo il numero di triangoli necessari per rappresentare una determinata forma.
Geolocalizzazione e Mappatura
Sebbene meno diretta, la trigonometria, strettamente legata ai triangoli rettangoli, trova applicazioni nella geolocalizzazione e nella mappatura. La capacità di calcolare distanze e angoli basandosi su punti di riferimento triangolari è alla base di molti sistemi di navigazione e di rilevamento topografico. Comprendere le proprietà dei triangoli rettangoli e delle loro circonferenze inscritte fornisce una base solida per lo sviluppo di algoritmi di posizionamento precisi.
Esempio Pratico
Consideriamo un triangolo rettangolo con cateti di lunghezza a = 6 e b = 8. L'ipotenusa c può essere calcolata utilizzando il teorema di Pitagora: c = √(a² + b²) = √(6² + 8²) = √(36 + 64) = √100 = 10.
Ora, possiamo calcolare il raggio della circonferenza inscritta usando la formula r = (a + b - c) / 2:
r = (6 + 8 - 10) / 2 = (14 - 10) / 2 = 4 / 2 = 2
Quindi, il raggio della circonferenza inscritta in questo triangolo rettangolo è 2.
Inoltre, possiamo calcolare l'area del triangolo come A = (1/2) * a * b = (1/2) * 6 * 8 = 24 e il semiperimetro come s = (6 + 8 + 10) / 2 = 12. Utilizzando la formula r = A / s, otteniamo r = 24 / 12 = 2, confermando il risultato precedente.
Conclusioni
La circonferenza inscritta in un triangolo rettangolo è un concetto geometrico ricco di proprietà e applicazioni pratiche. La sua comprensione offre strumenti preziosi per risolvere problemi in diversi settori, dall'architettura all'ingegneria, dalla computer grafica alla navigazione. La capacità di calcolare il raggio e la posizione dell'incentro è fondamentale per sfruttare appieno le potenzialità di questa figura geometrica.
Invitiamo i lettori ad approfondire ulteriormente lo studio della geometria e della trigonometria, esplorando le numerose connessioni tra questi campi e le loro applicazioni nel mondo reale. La matematica non è solo un insieme di formule, ma uno strumento potente per comprendere e modellare la realtà che ci circonda.