Circonferenza Inscritta In Un Triangolo Equilatero
Ti sei mai chiesto come disegnare un cerchio perfettamente all'interno di un triangolo equilatero, toccando tutti e tre i lati? Non è solo una questione di estetica geometrica; comprendere questa relazione può sbloccare un mondo di proprietà matematiche e applicazioni pratiche. Molti studenti, e anche appassionati di geometria, si trovano di fronte alla sfida di visualizzare e calcolare le dimensioni esatte di questa circonferenza inscritta. Ma non temere, la soluzione è più accessibile di quanto pensi!
Questo articolo ti guiderà passo dopo passo attraverso il processo, fornendoti gli strumenti necessari per comprendere, calcolare e persino disegnare una circonferenza inscritta in un triangolo equilatero. Che tu stia preparando un esame di geometria, lavorando a un progetto di design o semplicemente sei curioso di esplorare le meraviglie della matematica, sei nel posto giusto.
Cos'è una Circonferenza Inscritta?
Prima di addentrarci nei dettagli specifici del triangolo equilatero, chiariamo cosa intendiamo per "circonferenza inscritta". Una circonferenza inscritta, a volte chiamata anche incerchio, è una circonferenza che si trova all'interno di un poligono (in questo caso, un triangolo) e tocca ogni lato del poligono in un solo punto. Questi punti di contatto sono detti punti di tangenza.
Immagina un pallone perfettamente posizionato all'interno di un campo di calcio triangolare, toccando ciascun lato del campo. Ecco, hai visualizzato una circonferenza inscritta!
Il centro della circonferenza inscritta è chiamato incentro. Una delle proprietà fondamentali dell'incentro è che è il punto di incontro delle bisettrici degli angoli del triangolo. Questa proprietà è cruciale per la costruzione e il calcolo del raggio della circonferenza inscritta.
Triangolo Equilatero: Un Caso Speciale
Un triangolo equilatero è un triangolo con tutti e tre i lati di uguale lunghezza e tutti e tre gli angoli di 60 gradi. Questa simmetria rende il calcolo della circonferenza inscritta particolarmente semplice.
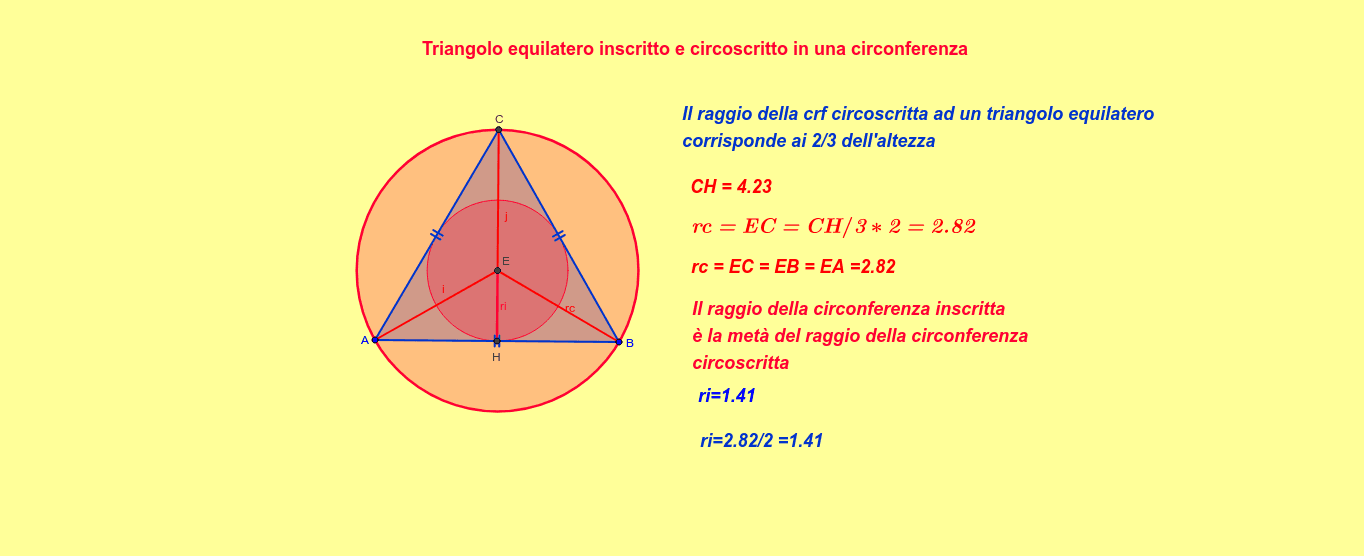
La simmetria del triangolo equilatero implica che l'incentro, il circocentro (il centro della circonferenza circoscritta) e l'ortocentro (il punto di incontro delle altezze) coincidono in un unico punto. Questo semplifica notevolmente i calcoli.
Calcolo del Raggio della Circonferenza Inscritta
Il raggio (r) della circonferenza inscritta in un triangolo equilatero può essere calcolato in diversi modi. Il metodo più comune utilizza la lunghezza del lato (l) del triangolo:
r = l / (2 * √3)
Vediamo come deriva questa formula:
1. L'altezza (h) di un triangolo equilatero è data da: h = (l * √3) / 2.
2. L'incentro di un triangolo equilatero divide l'altezza in un rapporto 2:1. Questo significa che il raggio della circonferenza inscritta è 1/3 dell'altezza.
3. Quindi, r = h / 3 = ((l * √3) / 2) / 3 = l / (2 * √3).
Esempio: Supponiamo di avere un triangolo equilatero con un lato di lunghezza 6 cm. Il raggio della circonferenza inscritta sarebbe: r = 6 / (2 * √3) = 3 / √3 = √3 cm (circa 1.73 cm).
Un Approccio Alternativo: Area e Semi-perimetro
Un'altra formula generale per il raggio della circonferenza inscritta, valida per qualsiasi triangolo, utilizza l'area (A) e il semi-perimetro (s) del triangolo:
r = A / s
Dove il semi-perimetro è metà del perimetro: s = (a + b + c) / 2 (dove a, b e c sono le lunghezze dei lati del triangolo).
Nel caso del triangolo equilatero, questa formula si semplifica perché tutti i lati sono uguali (a = b = c = l), quindi s = (3 * l) / 2.
L'area di un triangolo equilatero è: A = (l² * √3) / 4.
Sostituendo questi valori nella formula generale, otteniamo:
r = ((l² * √3) / 4) / ((3 * l) / 2) = (l² * √3 * 2) / (4 * 3 * l) = l / (2 * √3).
Come vedi, otteniamo lo stesso risultato, confermando la consistenza delle formule.
Come Disegnare una Circonferenza Inscritta in un Triangolo Equilatero
Ora che abbiamo compreso come calcolare il raggio, vediamo come disegnare effettivamente la circonferenza inscritta:
Passo 1: Disegna il Triangolo Equilatero. Usa un compasso e un righello per creare un triangolo con tutti i lati di uguale lunghezza. Assicurati che gli angoli siano di 60 gradi.
Passo 2: Trova l'Incentro. Puoi farlo in due modi:
a) Disegna le Bisettrici degli Angoli: Usa un compasso per disegnare le bisettrici di due angoli qualsiasi del triangolo. Il punto in cui si intersecano è l'incentro.
b) Trova il Punto Medio di un Lato e Traccia l'Altezza: Trova il punto medio di un lato e traccia una linea perpendicolare da quel punto medio al vertice opposto. Questa è un'altezza. L'incentro si troverà su questa altezza ad un terzo della distanza dal lato alla vertice.
Passo 3: Calcola il Raggio. Usa la formula r = l / (2 * √3) per calcolare il raggio della circonferenza inscritta.
Passo 4: Disegna la Circonferenza. Posiziona la punta del compasso sull'incentro. Imposta la larghezza del compasso al raggio calcolato. Disegna la circonferenza.
Verifica: La circonferenza dovrebbe toccare ciascun lato del triangolo in un solo punto. Se non è così, controlla i tuoi calcoli e la precisione del tuo disegno.
Applicazioni Pratiche
La comprensione della circonferenza inscritta non è solo un esercizio teorico. Ha diverse applicazioni pratiche in vari campi:
Architettura e Ingegneria: La geometria dei triangoli equilateri e delle circonferenze inscritte può essere utilizzata nella progettazione di strutture, ponti e altri elementi architettonici.
Design: La simmetria e l'equilibrio visivo creati da questa relazione geometrica possono essere sfruttati nel design grafico, nel design del prodotto e nell'arte.
Ottimizzazione: In alcuni problemi di ottimizzazione, trovare la circonferenza inscritta più grande possibile può essere una parte della soluzione. Ad esempio, nel taglio di materiali.
Conclusione
La circonferenza inscritta in un triangolo equilatero è un concetto geometrico elegante e potente. La sua comprensione non solo arricchisce la tua conoscenza della geometria, ma ti fornisce anche strumenti pratici per affrontare problemi in diversi campi. Spero che questo articolo ti abbia fornito una chiara comprensione del concetto, delle formule necessarie e delle applicazioni pratiche. Non aver paura di sperimentare, disegnare e calcolare! La geometria è un mondo affascinante che aspetta solo di essere esplorato.
Ricorda, la chiave per padroneggiare la geometria è la pratica costante. Risolvi esercizi, disegna figure e metti in pratica le formule. Con il tempo e la dedizione, diventerai un esperto nella circonferenza inscritta e in molti altri concetti geometrici.
Infine, non dimenticare che la matematica è ovunque intorno a noi. Guardati intorno e scopri come i concetti geometrici come questo si manifestano nel mondo reale. Sarai sorpreso di quanto spesso li incontrerai! Buona fortuna e buon divertimento con la geometria!