Che Cosa Sono I Numeri Primi

Ti sei mai chiesto come internet, la crittografia, o persino i giochi che ami, funzionano dietro le quinte? Una parte fondamentale di tutto ciò è legata a un concetto matematico affascinante e apparentemente semplice: i numeri primi. Molte persone li incontrano a scuola e poi li dimenticano, pensando che siano solo un esercizio di matematica teorica. Ma la verità è che i numeri primi sono ovunque, anche se non li vediamo direttamente. E capire cosa sono può aprirti una finestra su un mondo sorprendentemente potente.

Cosa sono i Numeri Primi? La Definizione Chiave

La definizione di un numero primo è piuttosto precisa: un numero primo è un numero intero maggiore di 1 che ha solo due divisori: 1 e se stesso.

Cosa significa questo? Significa che se provi a dividere un numero primo per qualsiasi altro numero (tranne 1 e se stesso), otterrai sempre un resto.

Esempi:

• 2 è un numero primo perché è divisibile solo per 1 e 2.
• 3 è un numero primo perché è divisibile solo per 1 e 3.
• 5 è un numero primo perché è divisibile solo per 1 e 5.
• 7 è un numero primo perché è divisibile solo per 1 e 7.

Controesempi:

• 4 non è un numero primo perché è divisibile per 1, 2 e 4.
• 6 non è un numero primo perché è divisibile per 1, 2, 3 e 6.
• 9 non è un numero primo perché è divisibile per 1, 3 e 9.

Spero che ora la definizione sia più chiara. Il "maggiore di 1" è importante: 1 non è un numero primo. Ricorda, deve avere esattamente due divisori.

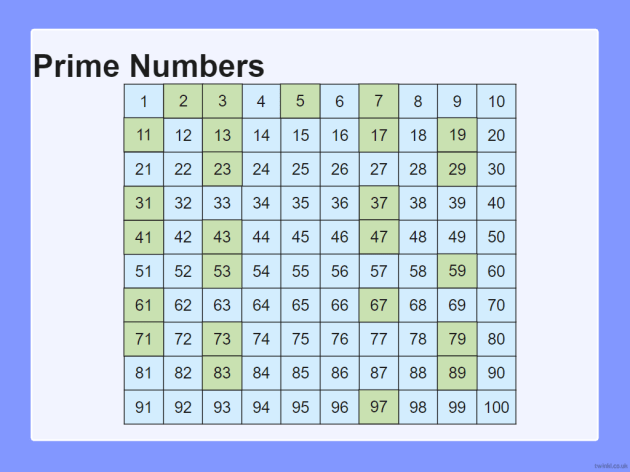
Come Identificare i Numeri Primi: Il Crivello di Eratostene

Esiste un metodo antico, ma ancora molto utile, per trovare i numeri primi all'interno di un determinato intervallo: il Crivello di Eratostene. Prende il nome dal matematico greco Eratostene di Cirene (circa 276-194 a.C.).

Ecco come funziona:

1. Scrivi tutti i numeri interi a partire da 2 fino al numero che vuoi testare (ad esempio, fino a 100).
2. Il primo numero della lista è 2, che è un numero primo. Cerchia 2.
3. Cancella tutti i multipli di 2 (4, 6, 8, 10, ecc.).
4. Il prossimo numero non cancellato è 3, che è un numero primo. Cerchia 3.
5. Cancella tutti i multipli di 3 (6, 9, 12, 15, ecc.). Nota che alcuni numeri potrebbero già essere cancellati.
6. Continua questo processo. Il prossimo numero non cancellato è 5, cerchialo e cancella tutti i suoi multipli.
7. Ripeti finché non hai cerchiato tutti i numeri primi e cancellato tutti i loro multipli.
8. I numeri rimasti non cancellati e cerchiati sono tutti i numeri primi nell'intervallo che hai considerato.

Il Crivello di Eratostene è un metodo efficiente per trovare numeri primi entro un intervallo limitato. Per numeri molto grandi, esistono algoritmi più avanzati, ma il principio è lo stesso: identificare e eliminare i numeri compositi (cioè i numeri non primi).

Perché i Numeri Primi Sono Così Importanti? La Teoria Fondamentale dell'Aritmetica

La vera potenza dei numeri primi risiede in un teorema fondamentale della matematica: la Teoria Fondamentale dell'Aritmetica. Questa teoria afferma che ogni numero intero maggiore di 1 può essere espresso come un prodotto unico di numeri primi.

Esempi:

• 12 = 2 x 2 x 3 (o 2² x 3)
• 30 = 2 x 3 x 5
• 100 = 2 x 2 x 5 x 5 (o 2² x 5²)

Questo significa che i numeri primi sono i mattoni fondamentali di tutti gli altri numeri interi. Proprio come puoi costruire qualsiasi parola usando le lettere dell'alfabeto, puoi costruire qualsiasi numero intero usando i numeri primi.

L'unicità della scomposizione è cruciale. C'è solo un modo per esprimere un numero come prodotto di numeri primi (a meno di cambiare l'ordine dei fattori). Questa proprietà è ciò che rende i numeri primi così utili in molti campi.

Numeri Primi e Crittografia: Proteggere le Nostre Informazioni

Uno degli usi più importanti dei numeri primi è nella crittografia, in particolare nella crittografia a chiave pubblica, come il sistema RSA (Rivest–Shamir–Adleman). Questo sistema, e altri simili, si basa sulla difficoltà di fattorizzare numeri molto grandi in numeri primi.

Ecco una semplificazione di come funziona:

1. Scegli due numeri primi molto grandi, chiamiamoli p e q.
2. Calcola n = p x q. Questo numero n è la chiave pubblica. Puoi condividerla con chiunque.
3. Esiste un'altra chiave, la chiave privata, che è correlata a p e q. Questa chiave privata la tieni segreta.
4. Per criptare un messaggio, si usa la chiave pubblica (n).
5. Per decriptare il messaggio, si usa la chiave privata.

La sicurezza del sistema RSA si basa sul fatto che è estremamente difficile (e dispendioso in termini di tempo di calcolo) trovare i fattori primi p e q di un numero n molto grande (ad esempio, con centinaia o migliaia di cifre). Anche i computer più potenti impiegherebbero anni o secoli per farlo.

Quindi, ogni volta che fai un acquisto online, invii un'email sicura o accedi al tuo conto bancario, i numeri primi stanno lavorando dietro le quinte per proteggere le tue informazioni.

Curiosità sui Numeri Primi: Infinità e Distribuzione

Ci sono alcune curiosità affascinanti sui numeri primi:

• Infinità: Esistono infiniti numeri primi. Questo è stato dimostrato da Euclide più di 2000 anni fa. La dimostrazione è elegante e relativamente semplice.
• Distribuzione: La distribuzione dei numeri primi è irregolare. Ci sono intervalli in cui i numeri primi sono molto vicini tra loro (ad esempio, 3 e 5, 5 e 7), e intervalli in cui sono molto distanti. Trovare un modello nella loro distribuzione è una delle grandi sfide della matematica.
• Numeri Primi Gemelli: Sono coppie di numeri primi che differiscono di 2 (ad esempio, 3 e 5, 5 e 7, 11 e 13). Non si sa se esistano infiniti numeri primi gemelli. Questa è una delle congetture irrisolte più famose della teoria dei numeri.

La distribuzione dei numeri primi è un argomento di ricerca attivo nella matematica. Il Teorema dei Numeri Primi fornisce un'approssimazione della quantità di numeri primi inferiori a un dato numero. Tuttavia, trovare una formula precisa per generare tutti i numeri primi è un sogno che i matematici inseguono da secoli.

Numeri Primi nel Mondo Reale: Oltre la Crittografia

Sebbene la crittografia sia l'applicazione più nota, i numeri primi hanno anche altri usi, a volte sorprendenti:

• Generazione di Numeri Casuali: Alcuni algoritmi per generare numeri casuali utilizzano numeri primi.
• Tabelle Hash: Nell'informatica, i numeri primi sono usati nelle tabelle hash per distribuire uniformemente i dati e ridurre le collisioni.
• Cicli di Vita delle Cicale: Alcune specie di cicale hanno cicli di vita che sono numeri primi (ad esempio, 13 anni o 17 anni). Si teorizza che questo sia un meccanismo di sopravvivenza per evitare di sincronizzare i loro cicli di vita con quelli dei predatori.

Questi esempi dimostrano che i numeri primi, pur essendo un concetto matematico astratto, hanno applicazioni pratiche in molti aspetti della nostra vita.

Conclusione: Apprezzare la Bellezza e l'Utilità dei Numeri Primi

Spero che questo articolo ti abbia aiutato a capire meglio cosa sono i numeri primi, perché sono importanti e come vengono utilizzati. La prossima volta che utilizzi internet o pensi a un problema di matematica, ricordati dei numeri primi: i mattoni fondamentali del mondo digitale e di molto altro.

Nonostante la loro apparente semplicità, i numeri primi nascondono una profondità e una complessità che continuano a sfidare e affascinare i matematici. La loro importanza nella crittografia li rende essenziali per la sicurezza delle nostre comunicazioni online. E la loro presenza inaspettata in altri campi, come la biologia, dimostra che la matematica è veramente il linguaggio dell'universo.

Quindi, la prossima volta che ti imbatti in un numero primo, fermati un attimo ad apprezzare la sua bellezza e la sua potenza. Potresti essere sorpreso da quanto sia pervasivo questo concetto fondamentale nella nostra vita quotidiana.