Che Cos è La Radice Quadrata

Hai mai pensato a come calcoliamo l'area di un quadrato sapendo solo la lunghezza del suo lato? Oppure, viceversa, come possiamo risalire alla lunghezza del lato conoscendo l'area? Ecco, la radice quadrata è lo strumento matematico che ci permette di fare proprio questo! In questo articolo, esploreremo in dettaglio cos'è la radice quadrata, come si calcola e dove la incontriamo nella vita di tutti i giorni. Questo articolo è pensato per studenti delle scuole medie e superiori, ma anche per chiunque abbia un po' di curiosità per la matematica e voglia rinfrescare le proprie conoscenze.

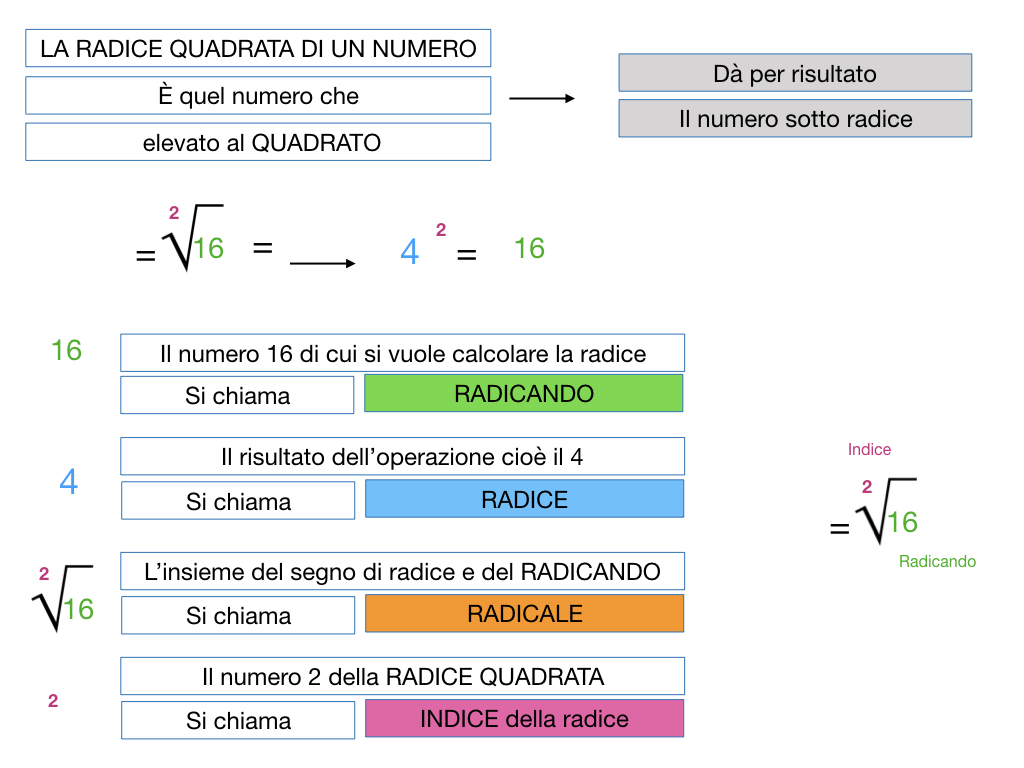
Cos'è la Radice Quadrata?

La radice quadrata di un numero, diciamo x, è quel numero che, moltiplicato per se stesso, dà come risultato x. In altre parole, è l'operazione inversa dell'elevamento al quadrato. Immagina un quadrato perfetto: la radice quadrata dell'area di quel quadrato è la lunghezza di uno dei suoi lati.

Matematicamente, la radice quadrata di x si indica con il simbolo √x. Quindi, se abbiamo √9 = 3, significa che 3 moltiplicato per 3 (3²) è uguale a 9.

Definizione Formale

Formalmente, la radice quadrata di un numero non negativo x è un numero non negativo y tale che y² = x. Questo è cruciale: la radice quadrata di un numero reale *negativo* non è un numero reale (ma un numero immaginario, che fa parte dei numeri complessi - un argomento per un'altra volta!).

Radice Quadrata Perfetta

Un quadrato perfetto è un numero intero che può essere espresso come il quadrato di un altro numero intero. Ad esempio, 4, 9, 16, 25 sono quadrati perfetti perché:

4 = 2²
9 = 3²
16 = 4²
25 = 5²

Trovare la radice quadrata di un quadrato perfetto è relativamente semplice, dato che si tratta semplicemente di identificare quel numero intero che, elevato al quadrato, dà il quadrato perfetto di partenza.

Come Calcolare la Radice Quadrata

Esistono diversi metodi per calcolare la radice quadrata di un numero. Vediamo i più comuni:

1. Tentativi ed Errori (per numeri piccoli)

Questo metodo è utile per numeri piccoli e quadrati perfetti. Si tratta di indovinare un numero, elevarlo al quadrato e vedere se il risultato si avvicina al numero di cui vogliamo calcolare la radice. Ad esempio, se vogliamo calcolare la radice quadrata di 25, possiamo provare:

4² = 16 (troppo piccolo)
5² = 25 (esatto!)

Quindi, √25 = 5.

2. Fattorizzazione in Numeri Primi

Questo metodo è utile per numeri più grandi. Consiste nel scomporre il numero in fattori primi. Se ogni fattore primo compare un numero pari di volte, allora il numero è un quadrato perfetto e la radice quadrata è il prodotto dei fattori primi presi una sola volta.

Ad esempio, calcoliamo la radice quadrata di 36:

Scomposizione in fattori primi: 36 = 2 x 2 x 3 x 3 = 2² x 3²
Radice quadrata: √36 = √(2² x 3²) = 2 x 3 = 6

3. Algoritmo di Estrazione di Radice Quadrata

Questo è un metodo più formale e preciso, utilizzato soprattutto per calcolare la radice quadrata di numeri non perfetti. È un po' più complesso, ma garantisce una buona approssimazione.

Non lo spiegheremo nel dettaglio qui, ma puoi trovare facilmente guide e tutorial online che illustrano passo dopo passo l'algoritmo.

4. Calcolatrice

Il metodo più semplice e veloce è sicuramente utilizzare una calcolatrice. La maggior parte delle calcolatrici scientifiche ha un tasto dedicato alla radice quadrata (solitamente indicato con il simbolo √). Basta inserire il numero di cui si vuole calcolare la radice e premere il tasto.

Dove Incontriamo la Radice Quadrata nella Vita di Tutti i Giorni?

La radice quadrata non è solo un concetto astratto della matematica. La incontriamo in molte situazioni pratiche:

Geometria: Come abbiamo visto all'inizio, per calcolare la lunghezza del lato di un quadrato conoscendo la sua area. Oppure, nel calcolo della diagonale di un quadrato (la diagonale è uguale al lato moltiplicato per √2). Il Teorema di Pitagora, fondamentale per calcolare la lunghezza dei lati di un triangolo rettangolo, utilizza la radice quadrata: a² + b² = c², quindi c = √(a² + b²).
Fisica: Nel calcolo della velocità di un oggetto in caduta libera (la velocità è proporzionale alla radice quadrata dell'altezza).
Ingegneria: Nel calcolo delle tensioni e delle deformazioni nei materiali.
Statistica: Nel calcolo della deviazione standard, una misura della dispersione dei dati rispetto alla media.
Informatica: In alcuni algoritmi di elaborazione delle immagini e dei segnali.

Pensiamo, ad esempio, a un carpentiere che deve costruire una mensola quadrata che abbia una superficie di 400 cm². Per sapere quanto deve tagliare il legno per ogni lato, dovrà calcolare la radice quadrata di 400, che è 20 cm. Oppure, immagina di voler piantare un albero al centro di un giardino quadrato. Se conosci la superficie del giardino, puoi calcolare la lunghezza del lato e quindi trovare il punto centrale.

Esempi Pratici e Risoluzione di Problemi

Vediamo alcuni esempi pratici per consolidare la nostra comprensione della radice quadrata:

Problema 1: Un quadrato ha un'area di 64 cm². Quanto misura il suo lato?
- Soluzione: Il lato del quadrato è la radice quadrata dell'area. Quindi, √64 = 8 cm.
Problema 2: Un triangolo rettangolo ha i cateti che misurano 3 cm e 4 cm. Quanto misura l'ipotenusa?
- Soluzione: Applichiamo il teorema di Pitagora: c = √(a² + b²) = √(3² + 4²) = √(9 + 16) = √25 = 5 cm.
Problema 3: Stai progettando un giardino quadrato e vuoi che abbia un'area di 100 metri quadrati. Quanto deve essere lungo ogni lato del giardino?
- Soluzione: Ogni lato deve essere lungo √100 = 10 metri.

Consigli Utili

Memorizza i quadrati perfetti: Conoscere i quadrati perfetti più comuni (1, 4, 9, 16, 25, 36, 49, 64, 81, 100, ecc.) ti aiuterà a calcolare rapidamente le radici quadrate di questi numeri.
Utilizza la stima: Se devi calcolare la radice quadrata di un numero che non è un quadrato perfetto, prova a stimare tra quali quadrati perfetti si trova. Ad esempio, √50 si trova tra √49 (7) e √64 (8).
Esercitati: Come per ogni concetto matematico, la pratica rende perfetti! Risolvi molti esercizi e problemi per familiarizzare con il calcolo delle radici quadrate.
Non aver paura di usare la calcolatrice: Per numeri complessi o quando hai bisogno di un risultato preciso, non esitare a usare la calcolatrice.

Conclusione

La radice quadrata è un concetto fondamentale della matematica con molte applicazioni pratiche nella vita di tutti i giorni. Che tu stia calcolando la lunghezza di un lato di un quadrato, applicando il teorema di Pitagora o analizzando dati statistici, la radice quadrata è uno strumento prezioso. Speriamo che questo articolo ti abbia fornito una comprensione chiara e completa di cos'è la radice quadrata, come si calcola e dove la puoi incontrare. Ora, armato di questa conoscenza, sei pronto ad affrontare nuove sfide matematiche e risolvere problemi reali in modo più efficiente!

Ricorda: la matematica è come un linguaggio. Più la pratichi, più diventi fluente. Quindi, continua ad esplorare, a sperimentare e a divertirti con i numeri!