Calcolare Lato Triangolo Conoscendo 2 Lati

Ti sei mai trovato di fronte a un problema di geometria, bloccato nel tentativo di calcolare il lato mancante di un triangolo, conoscendo solo gli altri due? Non sei solo. Molti studenti, professionisti e appassionati di matematica incontrano questa difficoltà. La geometria, con le sue formule e i suoi teoremi, può sembrare un labirinto, soprattutto quando si ha bisogno di una soluzione rapida e precisa. Capire come affrontare questo tipo di problema è fondamentale non solo per superare un esame, ma anche per applicare i principi geometrici in situazioni concrete della vita quotidiana.

Comprendere il Problema: Quali Triangoli Stiamo Considerando?

Prima di immergerci nelle formule, è essenziale definire il tipo di triangolo con cui abbiamo a che fare. I metodi di calcolo variano a seconda che si tratti di:

• Triangolo Rettangolo: Caratterizzato da un angolo di 90 gradi.
• Triangolo Isoscele: Con due lati di uguale lunghezza.
• Triangolo Equilatero: Con tutti i lati di uguale lunghezza.
• Triangolo Scaleno: Con tutti i lati di lunghezza diversa.

La tipologia di triangolo influenza direttamente la formula da utilizzare. Confondere le tipologie può portare a risultati errati. Ad esempio, applicare il Teorema di Pitagora a un triangolo non rettangolo genererebbe un errore significativo.

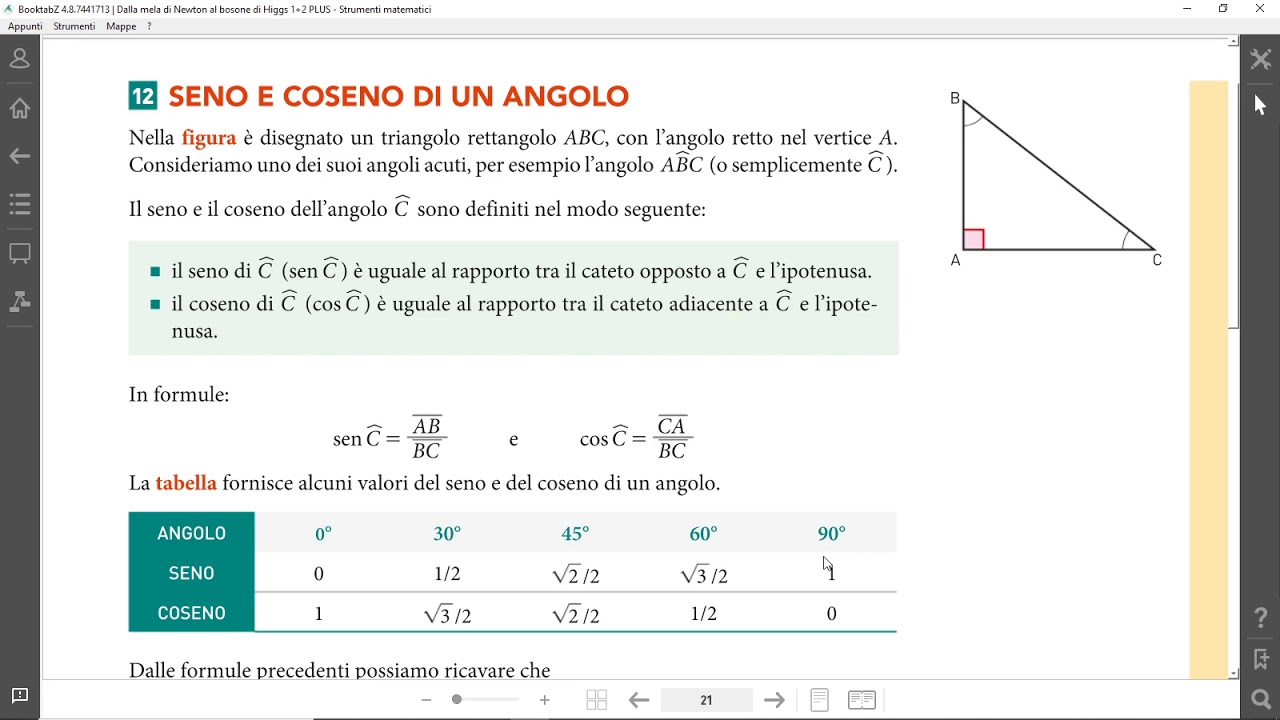
Il Teorema di Pitagora: La Chiave per i Triangoli Rettangoli

Il Teorema di Pitagora è lo strumento fondamentale per calcolare il lato mancante di un triangolo rettangolo. Afferma che la somma dei quadrati dei cateti (i due lati che formano l'angolo retto) è uguale al quadrato dell'ipotenusa (il lato opposto all'angolo retto). La formula è espressa come:

a² + b² = c²

Dove:

• a e b sono i cateti
• c è l'ipotenusa

Esempio pratico: Immagina di avere un triangolo rettangolo con un cateto di 3 cm e l'altro di 4 cm. Per trovare l'ipotenusa (c), applichiamo il teorema:

3² + 4² = c²

9 + 16 = c²

25 = c²

c = √25 = 5 cm

Quindi, l'ipotenusa del triangolo è di 5 cm.

La Legge dei Cosini: Un Approccio Più Generale

Ma cosa succede se il triangolo non è rettangolo? In questo caso, entra in gioco la Legge dei Cosini, uno strumento più potente e versatile. Questa legge generalizza il Teorema di Pitagora e può essere applicata a qualsiasi triangolo, a prescindere dagli angoli.

La legge dei cosini afferma che:

c² = a² + b² - 2ab * cos(γ)

Dove:

• a e b sono i lati noti
• c è il lato da calcolare
• γ è l'angolo opposto al lato c

Per applicare la Legge dei Cosini, è necessario conoscere due lati del triangolo e l'angolo compreso tra essi. Se si conoscono tutti e tre i lati, è possibile utilizzare la legge dei cosini per trovare gli angoli.

Esempio pratico: Supponiamo di avere un triangolo con lati a = 5 cm, b = 7 cm e l'angolo γ tra questi due lati è di 60 gradi. Per trovare il lato c, applichiamo la legge dei cosini:

c² = 5² + 7² - 2 * 5 * 7 * cos(60°)

c² = 25 + 49 - 70 * 0.5

c² = 74 - 35

c² = 39

c = √39 ≈ 6.24 cm

Quindi, il lato c del triangolo è approssimativamente 6.24 cm.

La Legge dei Seni: Un'Alternativa Utile

Un'altra risorsa importante è la Legge dei Seni. Questa legge stabilisce una relazione tra i lati di un triangolo e i seni dei loro angoli opposti. La formula è:

a / sin(α) = b / sin(β) = c / sin(γ)

Dove:

• a, b, e c sono i lati del triangolo
• α, β, e γ sono gli angoli opposti ai lati a, b, e c rispettivamente

La Legge dei Seni è utile quando si conoscono due angoli e un lato, oppure due lati e un angolo opposto a uno di essi. In quest'ultimo caso, bisogna prestare attenzione al cosiddetto "caso ambiguo," in cui potrebbero esserci due soluzioni possibili.

Esempio pratico: Supponiamo di conoscere un lato a = 8 cm, l'angolo α opposto a questo lato di 30 gradi, e un altro angolo β di 45 gradi. Per trovare il lato b, possiamo usare la legge dei seni:

8 / sin(30°) = b / sin(45°)

8 / 0.5 = b / 0.707

16 = b / 0.707

b = 16 * 0.707 ≈ 11.31 cm

Quindi, il lato b del triangolo è approssimativamente 11.31 cm.

Considerazioni sulle Unitá di Misura

È fondamentale assicurarsi che tutte le misure siano espresse nella stessa unità di misura prima di applicare qualsiasi formula. Se un lato è in metri e l'altro in centimetri, è necessario convertire una delle due misure per ottenere un risultato corretto. Utilizzare sempre le stesse unitá di misura!

Affrontare le Incertezze e le Approssimazioni

Nella vita reale, le misurazioni non sono sempre perfette. Spesso, si lavora con valori approssimati. È importante essere consapevoli dell'incertezza nelle misurazioni e di come questa incertezza può influenzare il risultato finale. Utilizzare un numero appropriato di cifre significative e arrotondare i risultati solo alla fine del calcolo per minimizzare gli errori di approssimazione.

Un'altra considerazione importante è che a volte, i dati forniti potrebbero essere insufficienti o contraddittori. Ad esempio, se si tenta di costruire un triangolo con lati che violano la disuguaglianza triangolare (la somma di due lati deve essere maggiore del terzo lato), il problema non avrà soluzione.

Contro-argomentazioni e Considerazioni Pratiche

Alcuni potrebbero sostenere che l'uso di software di geometria dinamica o calcolatrici online rende superfluo imparare queste formule. È vero che questi strumenti possono essere utili, ma la comprensione dei principi geometrici sottostanti è essenziale per interpretare correttamente i risultati e per risolvere problemi complessi che non possono essere affrontati con strumenti automatizzati. La conoscenza teorica offre un vantaggio competitivo e permette di sviluppare un pensiero critico e analitico.

Inoltre, la comprensione della geometria è fondamentale in molti campi, dall'architettura all'ingegneria, dal design alla programmazione grafica. La capacità di calcolare le dimensioni di un oggetto, di progettare una struttura stabile o di creare un'immagine realistica dipende dalla conoscenza dei principi geometrici.

Risoluzione dei Problemi: Un Approccio Sistematico

Quando si affronta un problema di geometria, è utile seguire un approccio sistematico:

• Comprendere il problema: Leggere attentamente il testo e identificare le informazioni note e ciò che si vuole calcolare.
• Disegnare un diagramma: Un disegno può aiutare a visualizzare il problema e a identificare le relazioni tra i lati e gli angoli.
• Scegliere la formula appropriata: Selezionare la formula più adatta in base al tipo di triangolo e alle informazioni disponibili.
• Sostituire i valori noti nella formula: Assicurarsi di utilizzare le stesse unità di misura.
• Risolvere l'equazione: Calcolare il valore del lato mancante.
• Verificare la risposta: Controllare se la risposta è ragionevole e coerente con le informazioni fornite.

Conclusione

Calcolare il lato di un triangolo conoscendo gli altri due può sembrare una sfida, ma con la comprensione dei principi fondamentali e l'applicazione delle formule appropriate, diventa un compito fattibile. Il Teorema di Pitagora, la Legge dei Cosini e la Legge dei Seni sono strumenti potenti che ci permettono di risolvere una vasta gamma di problemi geometrici. Ricorda, la pratica rende perfetti. Più esercizi risolvi, più acquisirai familiarità con le formule e più sarai in grado di applicarle in modo efficace.

Quali altre applicazioni della geometria ti incuriosiscono o vorresti approfondire?