Calcolare L'area Di Un Triangolo Rettangolo

Il calcolo dell'area di un triangolo rettangolo è un'operazione fondamentale in geometria e trova applicazioni in svariati campi, dall'architettura all'ingegneria, fino alla vita quotidiana. Comprendere il processo e la formula sottostante è essenziale per risolvere problemi pratici e teorici. In questo articolo, esploreremo in dettaglio come calcolare l'area di un triangolo rettangolo, analizzando la formula, fornendo esempi pratici e discutendo le sue applicazioni nel mondo reale.

Comprendere il Triangolo Rettangolo

Prima di addentrarci nel calcolo dell'area, è fondamentale capire cos'è un triangolo rettangolo. Un triangolo rettangolo è un triangolo che ha un angolo di 90 gradi, chiamato angolo retto. I due lati che formano l'angolo retto sono chiamati cateti, mentre il lato opposto all'angolo retto è chiamato ipotenusa.

Identificare i cateti è cruciale per il calcolo dell'area. Solitamente, si indicano i cateti con le lettere a e b, mentre l'ipotenusa viene indicata con c. La relazione tra i lati di un triangolo rettangolo è definita dal Teorema di Pitagora: a² + b² = c². Anche se il Teorema di Pitagora non è direttamente utilizzato nel calcolo dell'area, è fondamentale per la comprensione delle proprietà di un triangolo rettangolo.

La Formula per l'Area di un Triangolo Rettangolo

L'area di un triangolo rettangolo è data dalla seguente formula:

Area = (base * altezza) / 2

In un triangolo rettangolo, i due cateti possono essere considerati come base e altezza. Quindi, la formula può essere riscritta come:

Area = (a * b) / 2

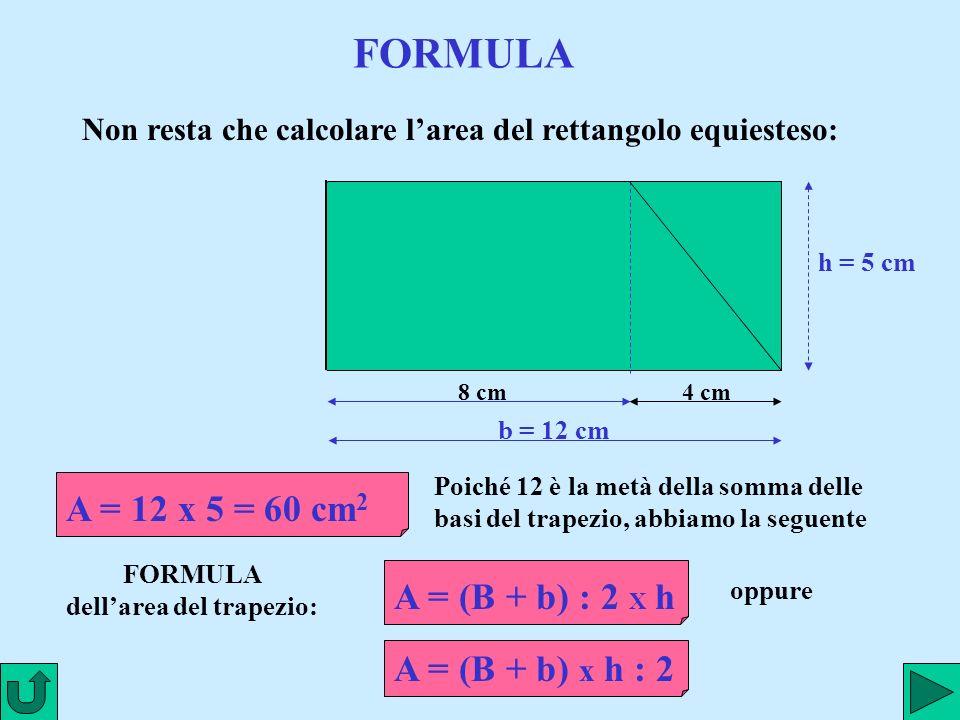
Dove a e b sono le lunghezze dei due cateti. Questa formula deriva dal fatto che un triangolo rettangolo può essere visto come metà di un rettangolo con lati di lunghezza a e b. L'area del rettangolo è a * b, e quindi l'area del triangolo rettangolo è la metà di quella del rettangolo.

Esempio Pratico

Supponiamo di avere un triangolo rettangolo con un cateto di 6 cm e l'altro di 8 cm. Per calcolare l'area, applichiamo la formula:

Area = (6 cm * 8 cm) / 2 = 48 cm² / 2 = 24 cm²

Quindi, l'area del triangolo rettangolo è di 24 centimetri quadrati.

Passaggi per Calcolare l'Area

Identificare i cateti: Individua i due lati che formano l'angolo retto nel triangolo.
Misurare i cateti: Determina la lunghezza di entrambi i cateti. Assicurati che le misure siano nella stessa unità (es. cm, metri, pollici).
Applicare la formula: Inserisci le lunghezze dei cateti nella formula: Area = (a * b) / 2.
Calcolare l'area: Esegui la moltiplicazione e la divisione per ottenere il valore dell'area.
Indicare l'unità di misura: Esprimi l'area con l'unità di misura appropriata (es. cm², m², in²).

Applicazioni nel Mondo Reale

Il calcolo dell'area di un triangolo rettangolo ha numerose applicazioni pratiche:

Architettura e Ingegneria: Gli architetti e gli ingegneri utilizzano i triangoli rettangoli per progettare edifici, ponti e altre strutture. Calcolare l'area dei triangoli formati dalle travi, dai supporti e dalle pareti è essenziale per determinare la quantità di materiali necessari e per garantire la stabilità della struttura.
Geodesia e Cartografia: Nella misurazione dei terreni e nella creazione di mappe, i triangoli rettangoli sono utilizzati per calcolare le aree di superfici irregolari. Dividendo una superficie complessa in triangoli rettangoli più piccoli, è possibile calcolare l'area totale sommando le aree dei singoli triangoli.
Falegnameria e Costruzioni: I falegnami utilizzano i triangoli rettangoli per tagliare il legno ad angoli precisi e per costruire strutture come tetti, scale e mobili. Calcolare l'area dei triangoli formati dai pezzi di legno è importante per determinare la quantità di materiale necessario e per ottimizzare il taglio.
Grafica e Design: Nel design grafico, i triangoli rettangoli sono utilizzati per creare forme, loghi e illustrazioni. Conoscere l'area di un triangolo rettangolo può aiutare i designer a dimensionare correttamente gli elementi grafici e a creare composizioni visivamente equilibrate.
Navigazione: In passato, la navigazione utilizzava spesso triangoli rettangoli e la trigonometria per calcolare distanze e posizioni. Anche se oggi esistono sistemi più avanzati, la comprensione dei principi geometrici alla base della navigazione è ancora utile.

Esempi Specifici

Calcolo dell'area di un tetto a falde: Un tetto a falde è spesso composto da triangoli rettangoli. Calcolare l'area di questi triangoli è fondamentale per determinare la quantità di tegole necessarie.
Progettazione di un giardino a forma di triangolo rettangolo: Se si desidera creare un giardino a forma di triangolo rettangolo, il calcolo dell'area è essenziale per determinare la quantità di terra necessaria e per pianificare la disposizione delle piante.
Costruzione di una rampa per disabili: La costruzione di una rampa per disabili richiede il rispetto di determinate pendenze e angolazioni. I triangoli rettangoli vengono utilizzati per calcolare la lunghezza della rampa e l'altezza da raggiungere.

Alternative per il Calcolo dell'Area

Sebbene la formula Area = (a * b) / 2 sia la più semplice e diretta per i triangoli rettangoli, esistono altre formule che possono essere utilizzate in situazioni in cui non si conoscono direttamente i cateti. Ad esempio:

Formula di Erone: Questa formula permette di calcolare l'area di un triangolo qualsiasi, conoscendo la lunghezza dei tre lati (a, b, c). La formula è: Area = √(s(s-a)(s-b)(s-c)), dove s è il semiperimetro del triangolo: s = (a + b + c) / 2. Anche se questa formula è valida per tutti i triangoli, per i triangoli rettangoli risulta più complessa della formula specifica.
Area = (1/2) * base * altezza: Questa è la formula generale per l'area di un triangolo. Se si conosce la lunghezza di un lato (la base) e l'altezza relativa a quel lato, si può calcolare l'area. In un triangolo rettangolo, se si conosce l'ipotenusa e l'altezza relativa all'ipotenusa, si può utilizzare questa formula, anche se in genere è più complesso determinare l'altezza relativa all'ipotenusa rispetto alla semplice misurazione dei cateti.

Considerazioni Importanti

Unità di misura: Assicurati che tutte le misure siano nella stessa unità prima di eseguire i calcoli. Se hai misure in centimetri e in metri, converti tutto in centimetri o in metri.
Arrotondamenti: Se le misure sono approssimate, presta attenzione agli arrotondamenti. Arrotonda solo alla fine del calcolo per evitare errori significativi.
Precisione: La precisione delle misure influisce sulla precisione del risultato. Utilizza strumenti di misura adeguati per ottenere risultati accurati.

Conclusione

Calcolare l'area di un triangolo rettangolo è un'operazione relativamente semplice, ma fondamentale in molti contesti. La formula Area = (a * b) / 2 è facile da ricordare e da applicare. Comprendere i concetti di base della geometria e le proprietà dei triangoli rettangoli è essenziale per risolvere problemi pratici e teorici. Che tu sia uno studente, un professionista o semplicemente una persona curiosa, padroneggiare il calcolo dell'area di un triangolo rettangolo ti fornirà uno strumento utile e versatile. Esercitati con diversi esempi e applica le tue conoscenze in situazioni reali per consolidare la tua comprensione. Ricorda, la pratica rende perfetti!