Calcolare La Frazione Di Un Numero Scuola Primaria

Ciao! Se sei qui, probabilmente stai aiutando tuo figlio o tua figlia (o magari sei tu che hai bisogno di una mano!) a capire le frazioni a scuola primaria. Capisco perfettamente: le frazioni possono sembrare un po' ostiche all'inizio. Non preoccuparti, non sei solo! Molti bambini (e anche adulti!) trovano le frazioni un argomento un po' difficile. Ma con un po' di pazienza e le giuste strategie, le frazioni diventeranno molto più chiare e gestibili.

Spesso, l'ostacolo principale è la mancanza di una comprensione concreta di cosa rappresenti realmente una frazione. Tendiamo a presentarle come meri simboli matematici, senza collegarle a esperienze reali. Ed è proprio questa connessione che fa la differenza!

Perché le Frazioni Sono Importanti?

Potresti chiederti: "Ma a cosa servono veramente le frazioni?". La risposta è: a tantissime cose! Non si tratta solo di un esercizio scolastico fine a se stesso. Le frazioni sono ovunque intorno a noi:

Cucinare: Seguire una ricetta spesso richiede l'uso di frazioni (ad esempio, 1/2 tazza di farina, 1/4 di cucchiaino di sale).
Condivisione: Dividere una pizza o una torta tra amici implica l'utilizzo di frazioni. Chi non vuole la sua giusta parte?
Misurazioni: Usiamo le frazioni quando misuriamo con righelli, metri o quando stimiamo il tempo ("Ci vediamo tra mezz'ora").
Musica: Il valore delle note musicali è espresso in frazioni (ad esempio, una semibreve, una minima, una semiminima).
Denaro: Anche se non ce ne rendiamo conto, i centesimi sono frazioni di un euro!

Quindi, imparare a lavorare con le frazioni non è solo un'abilità matematica, ma una competenza essenziale per la vita di tutti i giorni. Pensaci: se tuo figlio capisce le frazioni, sarà più autonomo e sicuro di sé in molte situazioni pratiche.

Cos'è una Frazione? Un'Analogia Utile

Immagina di avere una torta intera. Questa torta rappresenta l'intero, l'unità. Ora, immagina di tagliare la torta in 4 fette uguali. Ogni fetta rappresenta 1/4 (un quarto) della torta. La frazione è composta da due numeri:

Il numero sotto (il denominatore) indica in quante parti uguali è stato diviso l'intero (in questo caso, 4).
Il numero sopra (il numeratore) indica quante di queste parti stiamo considerando (in questo caso, 1 fetta).

Quindi, 1/4 significa che abbiamo preso una parte su quattro totali. Allo stesso modo, se prendiamo due fette, avremo 2/4 (due quarti) della torta. Se prendiamo tutte e quattro le fette, avremo 4/4, ovvero l'intera torta (l'intero!).

Frazioni Proprie, Improprie e Apparenti

È importante introdurre anche le diverse tipologie di frazioni, in modo graduale:

Frazioni Proprie: Il numeratore è minore del denominatore (es. 1/2, 3/4, 2/5). Rappresentano una parte minore dell'intero.
Frazioni Improprie: Il numeratore è maggiore o uguale al denominatore (es. 5/4, 3/2, 7/7). Rappresentano una parte uguale o maggiore dell'intero.
Frazioni Apparenti: Il numeratore è un multiplo del denominatore (es. 4/2, 6/3, 9/3). Rappresentano uno o più interi. Ad esempio, 4/2 è uguale a 2 interi.

Come Calcolare la Frazione di un Numero: Strategie Pratiche

Ora veniamo al punto cruciale: come si calcola concretamente la frazione di un numero? Ecco alcuni metodi, partendo dai più intuitivi:

Metodo Visivo: Oggetti Concreti e Disegni

Questo metodo è fondamentale per i bambini della scuola primaria, perché permette di visualizzare il concetto di frazione. Utilizza oggetti reali o disegni per rendere l'operazione più tangibile.

Esempio: Vogliamo calcolare 1/3 di 12 caramelle.

Prendiamo 12 caramelle e disponiamole sul tavolo.
Dobbiamo dividere le caramelle in 3 gruppi uguali (perché il denominatore è 3).
Contiamo quante caramelle ci sono in ogni gruppo. Ci saranno 4 caramelle per gruppo.
Quindi, 1/3 di 12 caramelle è uguale a 4 caramelle.

Lo stesso principio può essere applicato con i disegni. Disegna 12 cerchietti e dividili in 3 gruppi uguali. Conta quanti cerchietti ci sono in ogni gruppo. Il risultato sarà sempre 4.

Metodo della Divisione e Moltiplicazione

Questo metodo è più astratto, ma molto efficiente una volta compreso il concetto di base.

La regola generale è: Per calcolare la frazione di un numero, dividi il numero per il denominatore e poi moltiplica il risultato per il numeratore.

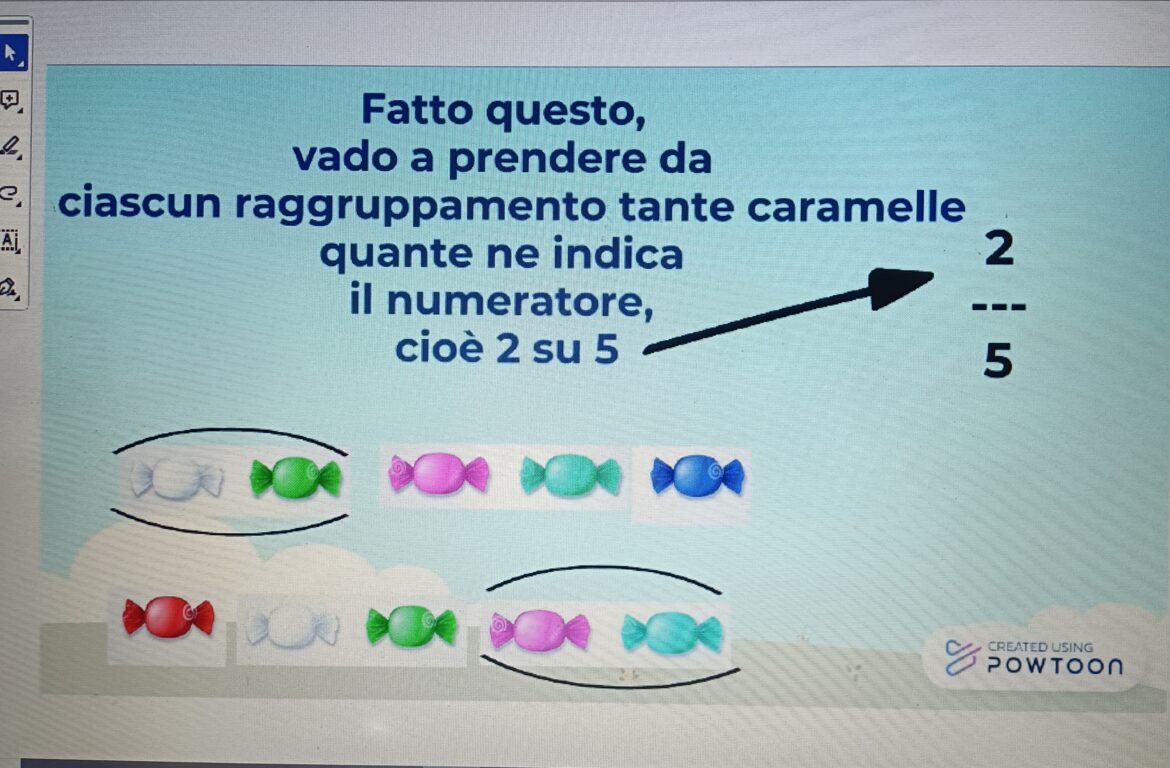
Esempio: Vogliamo calcolare 2/5 di 20.

Dividiamo 20 per il denominatore (5): 20 : 5 = 4
Moltiplichiamo il risultato (4) per il numeratore (2): 4 x 2 = 8
Quindi, 2/5 di 20 è uguale a 8.

Un altro esempio: Calcolare 3/4 di 16.

Dividiamo 16 per il denominatore (4): 16 : 4 = 4
Moltiplichiamo il risultato (4) per il numeratore (3): 4 x 3 = 12
Quindi, 3/4 di 16 è uguale a 12.

Metodo Pratico: Trovare l'Unità Frazionaria

Questo metodo si concentra sul trovare il valore di una singola parte (l'unità frazionaria) e poi moltiplicarlo per il numero di parti che ci interessano.

Esempio: Calcolare 2/3 di 15.

Troviamo quanto vale 1/3 di 15. Per farlo, dividiamo 15 per 3 (il denominatore): 15 : 3 = 5. Quindi, 1/3 di 15 è uguale a 5.
Ora che sappiamo che 1/3 è uguale a 5, moltiplichiamo 5 per 2 (il numeratore): 5 x 2 = 10.
Quindi, 2/3 di 15 è uguale a 10.

Errori Comuni e Come Evitarli

È importante essere consapevoli degli errori più comuni che i bambini commettono quando lavorano con le frazioni, in modo da poterli aiutare a evitarli.

Confondere Numeratore e Denominatore: Spesso i bambini invertono i due numeri, compromettendo il risultato. Ricorda loro sempre che il denominatore indica in quante parti è diviso l'intero e il numeratore quante parti stiamo considerando.
Non Capire il Concetto di "Parti Uguali": La frazione ha senso solo se l'intero è diviso in parti uguali. Insisti su questo concetto e fai esempi concreti.
Applicare le Operazioni con i Numeri Interi Alle Frazioni: Alcuni bambini cercano di applicare le stesse regole che usano con i numeri interi alle frazioni, il che porta a errori. Sottolinea che le frazioni richiedono regole specifiche.
Mancanza di Visualizzazione: Se un bambino ha difficoltà, torna sempre all'utilizzo di oggetti concreti o disegni per visualizzare il problema.

Consigli Extra per un Apprendimento Efficace

Ecco alcuni consigli aggiuntivi per rendere l'apprendimento delle frazioni più efficace e divertente:

Utilizza Giochi e Attività Interattive: Esistono molti giochi online e attività pratiche che possono rendere l'apprendimento delle frazioni più coinvolgente. Cerca risorse su internet o crea i tuoi giochi personalizzati.
Collega le Frazioni alla Vita Quotidiana: Sfrutta ogni occasione per parlare di frazioni nella vita di tutti i giorni. Ad esempio, quando cucinate insieme, chiedi a tuo figlio di aiutarti a misurare gli ingredienti utilizzando le frazioni.
Sii Paziente e Incoraggiante: L'apprendimento delle frazioni richiede tempo e pratica. Sii paziente con tuo figlio e incoraggialo a non arrendersi. Celebra i suoi progressi, anche quelli piccoli.
Suddividi il Problema: Se l'esercizio è troppo difficile, semplificalo suddividendolo in passaggi più piccoli.

Un Approccio Alternativo: Le Frazioni Come Rapporti

Un modo più avanzato di concepire le frazioni, utile per i bambini più grandi o per chi ha già una buona base, è vederle come rapporti. Un rapporto confronta due quantità. Ad esempio, la frazione 2/3 può essere vista come il rapporto tra 2 parti e 3 parti totali. Questo approccio è utile per affrontare problemi più complessi e per prepararsi alle proporzioni.

Controindicazioni: Presentare questo concetto troppo presto può confondere i bambini più piccoli. Assicurati che abbiano una solida comprensione delle frazioni come parti di un intero prima di introdurre l'idea del rapporto.

Ricorda che l'obiettivo finale è quello di aiutare tuo figlio a comprendere il concetto di frazione, non solo a memorizzare delle regole. Concentrati sulla comprensione, sull'esplorazione e sulla sperimentazione, e vedrai che le frazioni diventeranno un argomento molto più accessibile e interessante.

E ora, prova a mettere in pratica quello che hai imparato! Qual è la tua strategia preferita per spiegare le frazioni? E cosa fai quando tuo figlio/a incontra difficoltà? Condividi le tue esperienze e i tuoi trucchi!