Area Di Un Triangolo Inscritto In Una Circonferenza

Capita a tutti, prima o poi, di trovarsi di fronte a problemi di geometria apparentemente insormontabili. Uno di questi, che spesso crea qualche grattacapo, è il calcolo dell'area di un triangolo inscritto in una circonferenza. Non preoccuparti, non sei solo! Molti studenti e appassionati di matematica si sono scontrati con questa sfida. L'obiettivo di questo articolo è rendere questo concetto accessibile e comprensibile a tutti, fornendoti gli strumenti per affrontare questi problemi con sicurezza.

Spesso, la difficoltà risiede nel collegare le proprietà del triangolo con quelle della circonferenza. Magari ti chiedi: come faccio a sfruttare il raggio della circonferenza? Come posso usare le relazioni tra angoli e lati? Cercheremo di rispondere a queste domande in modo chiaro e graduale.

Perché Dovresti Preoccuparti dell'Area di un Triangolo Inscritto?

Potresti pensare che questo sia solo un esercizio di matematica astratta, ma in realtà il calcolo dell'area di un triangolo inscritto ha applicazioni pratiche in diversi campi. Ad esempio:

• Architettura: La progettazione di strutture complesse, come cupole e archi, spesso richiede la conoscenza delle relazioni geometriche tra triangoli e cerchi.
• Ingegneria: Nel design di ponti e altre strutture, è fondamentale calcolare le forze che agiscono su diverse parti. La trigonometria, e quindi la geometria dei triangoli, gioca un ruolo chiave.
• Grafica Computerizzata: La creazione di modelli 3D e animazioni spesso si basa su principi geometrici, inclusi quelli relativi a triangoli inscritti e circonferenze.
• Astronomia: Il calcolo delle distanze e delle posizioni degli oggetti celesti può coinvolgere la geometria sferica, che a sua volta si basa su concetti legati ai triangoli e ai cerchi.

Inoltre, comprendere questo argomento rafforza il tuo pensiero logico e le tue capacità di problem-solving, competenze utili in qualsiasi ambito della vita.

Formule e Metodi di Calcolo

Esistono diverse formule per calcolare l'area di un triangolo inscritto in una circonferenza, a seconda delle informazioni che hai a disposizione. Vediamone alcune:

1. Conoscendo i Lati (Formula di Erone)

Se conosci le lunghezze dei tre lati del triangolo (a, b, c), puoi utilizzare la formula di Erone:

Area = √(s(s-a)(s-b)(s-c))

Dove s è il semiperimetro del triangolo: s = (a + b + c) / 2

Questa formula è utile quando non hai informazioni sull'angolo o sul raggio della circonferenza.

2. Conoscendo un Lato e l'Angolo Opposto (Teorema dei Seni)

Il teorema dei seni stabilisce una relazione tra i lati di un triangolo e i seni degli angoli opposti:

a / sin(A) = b / sin(B) = c / sin(C) = 2R

Dove R è il raggio della circonferenza circoscritta. Se conosci un lato (ad esempio, a) e l'angolo opposto (A), puoi trovare il raggio: R = a / (2sin(A))

A questo punto, se conosci anche gli altri due lati (b e c), puoi utilizzare la formula standard dell'area: Area = (1/2) * b * c * sin(A). Oppure, se conosci altri angoli, puoi usare il teorema dei seni per trovare i lati mancanti.

3. Conoscendo il Raggio della Circonferenza e i Lati

Una formula molto utile lega l'area del triangolo al raggio della circonferenza circoscritta (R) e ai lati (a, b, c):

Area = (a * b * c) / (4R)

Questa formula è particolarmente efficace quando conosci il raggio e le lunghezze dei lati.

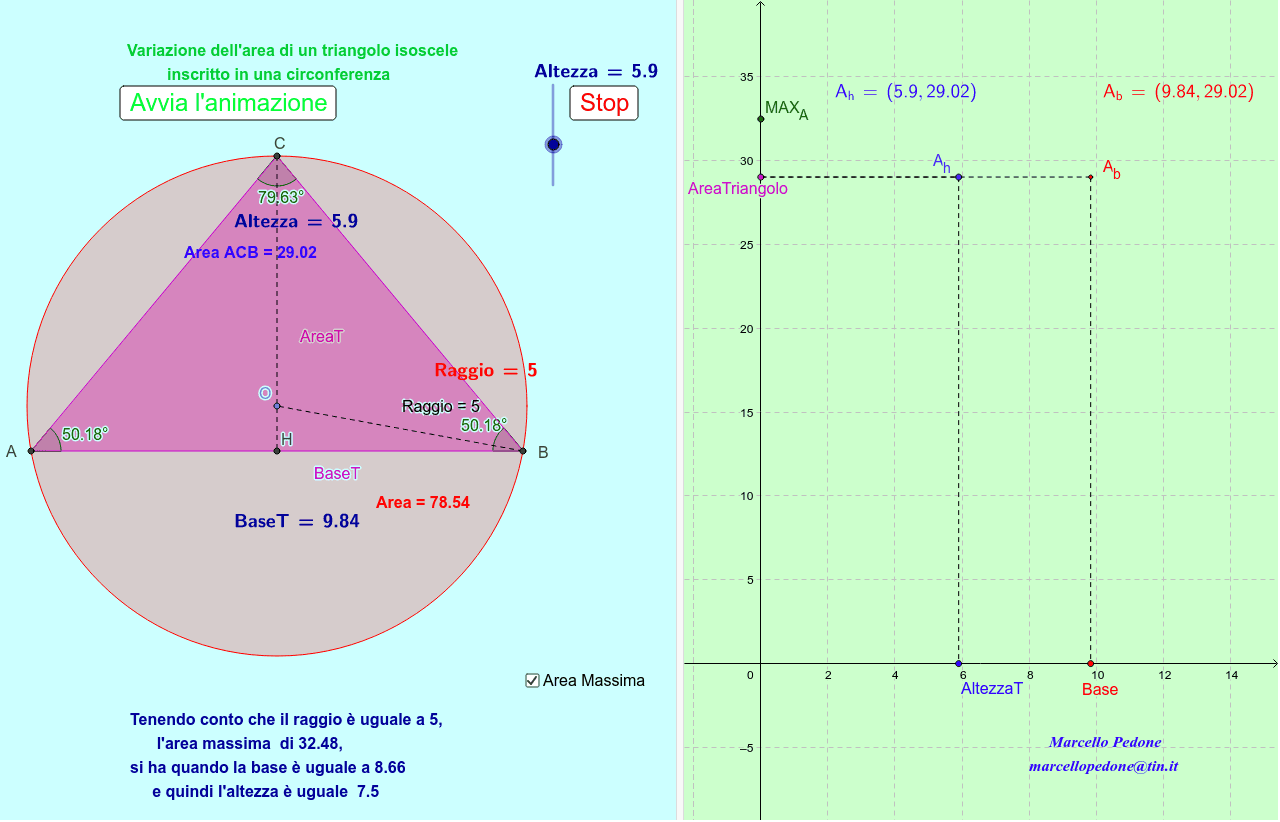
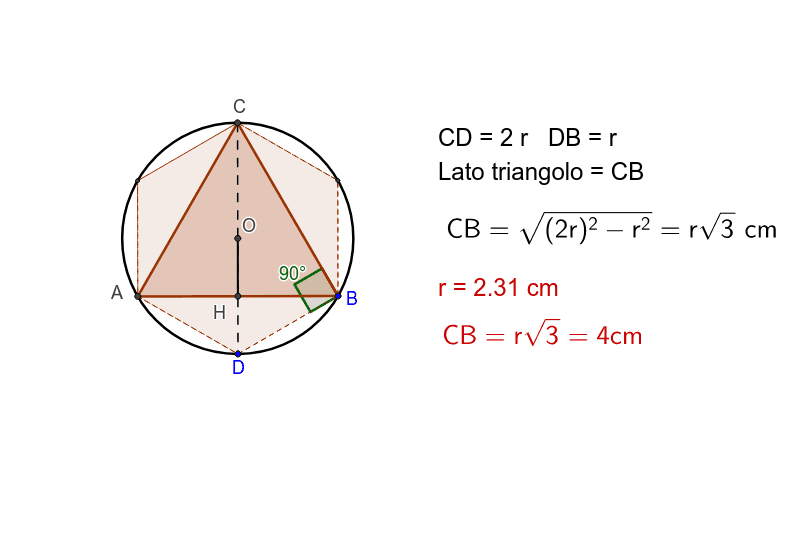
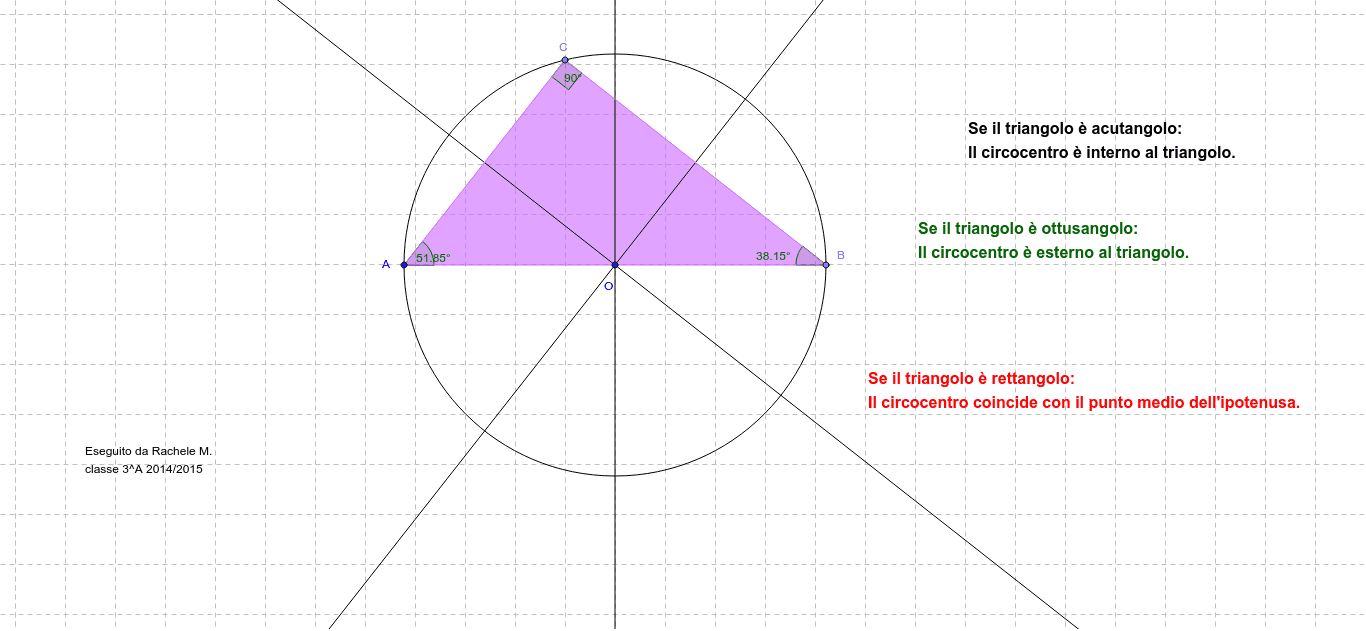
4. Triangolo Rettangolo Inscritto

Se il triangolo è rettangolo e inscritto in una circonferenza, l'ipotenusa coincide con il diametro della circonferenza. Questo semplifica notevolmente i calcoli. Se conosci i cateti (a e b), l'area è semplicemente:

Area = (1/2) * a * b

Inoltre, il raggio della circonferenza è la metà dell'ipotenusa: R = √(a² + b²) / 2

Esempio Pratico

Supponiamo di avere un triangolo inscritto in una circonferenza di raggio 5 cm. I lati del triangolo misurano 6 cm, 8 cm e 10 cm. Calcoliamo l'area utilizzando la formula Area = (a * b * c) / (4R):

Area = (6 * 8 * 10) / (4 * 5) = 480 / 20 = 24 cm²

Notiamo che questo è un triangolo rettangolo (perché 6² + 8² = 10²), quindi avremmo potuto calcolare l'area più semplicemente come (1/2) * 6 * 8 = 24 cm².

Affrontare le Obiezioni: Quando Queste Formule Non Funzionano?

È importante riconoscere i limiti di queste formule. Potresti pensare: "Ma cosa succede se non conosco abbastanza informazioni? Cosa succede se ho solo un angolo e un lato?"

In questi casi, è fondamentale utilizzare una combinazione di teoremi trigonometrici (come il teorema dei seni e il teorema del coseno) per ricavare le informazioni mancanti. A volte, potrebbe essere necessario risolvere un sistema di equazioni per trovare i lati e gli angoli necessari per applicare le formule dell'area. La chiave è analizzare attentamente le informazioni che hai e scegliere la strategia più adatta.

Consigli Utili per Risolvere i Problemi

• Disegna sempre un diagramma: Visualizzare il problema ti aiuta a capire le relazioni tra le diverse grandezze.
• Identifica le informazioni note: Scrivi chiaramente quali lati, angoli o il raggio della circonferenza conosci.
• Scegli la formula appropriata: In base alle informazioni che hai, seleziona la formula che ti permette di calcolare l'area.
• Applica i teoremi trigonometrici: Se non hai abbastanza informazioni, usa il teorema dei seni o del coseno per trovare i lati o gli angoli mancanti.
• Verifica la tua risposta: Assicurati che la tua risposta sia ragionevole e che abbia le unità di misura corrette.

Oltre la Teoria: Esercizi e Risorse Utili

La pratica è fondamentale per padroneggiare qualsiasi concetto matematico. Ecco alcune risorse che puoi utilizzare per esercitarti:

• Libri di testo di geometria: Cercare esercizi specifici sull'area di triangoli inscritti.
• Siti web di matematica: Molti siti offrono esercizi interattivi e tutorial.
• App per la matematica: Alcune app possono aiutarti a visualizzare i problemi e a risolverli passo dopo passo.
• Chiedi aiuto al tuo insegnante o a un tutor: Non esitare a chiedere chiarimenti se hai difficoltà.

Ricorda, la chiave è la perseveranza e la volontà di imparare. Non scoraggiarti se all'inizio incontri difficoltà. Con la pratica, diventerai sempre più abile nel calcolare l'area di triangoli inscritti in una circonferenza.

Un Ultimo Pensiero

Spero che questo articolo ti abbia fornito una comprensione più chiara e accessibile del calcolo dell'area di un triangolo inscritto in una circonferenza. Ricorda che la matematica non è solo una serie di formule, ma un modo per comprendere il mondo che ci circonda. Approccia i problemi con curiosità e determinazione, e sarai in grado di superare qualsiasi sfida.

Ora, rifletti su questo: in quali altri contesti della tua vita potresti applicare i principi geometrici e trigonometrici che hai imparato oggi? Come potresti utilizzare queste conoscenze per risolvere problemi reali?