Area Di Base Di Un Prisma

Ti sei mai trovato di fronte a un prisma e ti sei chiesto: "Come faccio a calcolare quest'area di base?". Non sei solo! Molti studenti e appassionati di geometria si scontrano con questo problema. Capire come determinare l'area di base di un prisma è fondamentale per calcolare il volume e l'area superficiale di questa solida figura geometrica. Questa guida ti aiuterà a navigare questo concetto con chiarezza e sicurezza.

Cos'è un Prisma e Perché l'Area di Base è Importante?

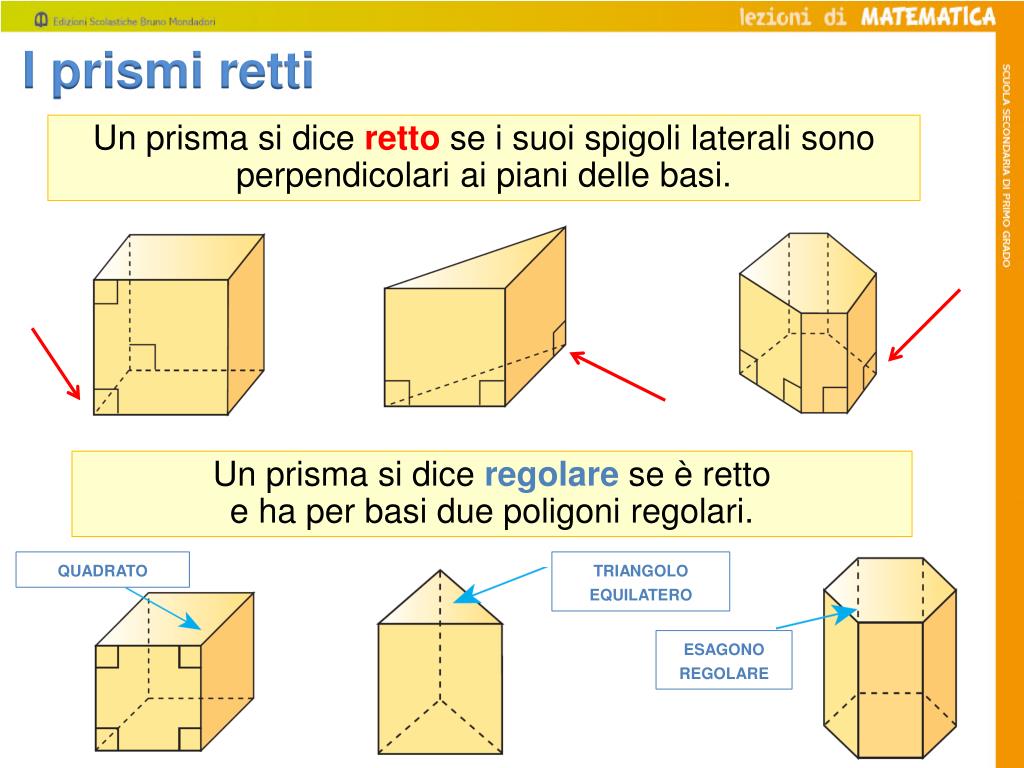
Prima di immergerci nei calcoli, cerchiamo di definire cos'è un prisma. Un prisma è un solido geometrico con due facce parallele e congruenti, chiamate basi, collegate da facce laterali che sono parallelogrammi. Le basi possono essere triangoli, quadrati, pentagoni, o qualsiasi altro poligono. Immagina una confezione di fazzoletti a forma triangolare: ecco un prisma triangolare! Oppure un classico mattone: un prisma rettangolare.

L'area di base è l'area di una di queste due facce congruenti. È un elemento cruciale per diversi motivi:

Calcolo del Volume: Il volume di un prisma si ottiene moltiplicando l'area di base per l'altezza del prisma (la distanza perpendicolare tra le due basi). Volume = Area di Base * Altezza.
Calcolo dell'Area Superficiale: Per calcolare l'area superficiale totale, devi conoscere l'area di base per sommarla all'area laterale.
Applicazioni Pratiche: Dalla progettazione architettonica alla misurazione di materiali da costruzione, la capacità di calcolare l'area di base di un prisma è un'abilità preziosa.

Come Calcolare l'Area di Base: Passo dopo Passo

Il metodo per calcolare l'area di base dipende interamente dalla forma della base. Analizziamo i casi più comuni:

Prisma a Base Triangolare

Se la base è un triangolo, l'area si calcola con la formula ben nota:

Area = (1/2) * base * altezza

Dove:

"base" è la lunghezza della base del triangolo.
"altezza" è l'altezza del triangolo (la distanza perpendicolare dalla base al vertice opposto).

Esempio: Supponiamo di avere un prisma con una base triangolare avente una base di 8 cm e un'altezza di 5 cm. L'area della base sarebbe (1/2) * 8 cm * 5 cm = 20 cm².

Consiglio: Se il triangolo è rettangolo, uno dei lati che formano l'angolo retto può essere considerato la base, e l'altro lato l'altezza.

Prisma a Base Quadrata o Rettangolare

Se la base è un quadrato o un rettangolo, il calcolo è ancora più semplice:

Area (Quadrato) = lato * lato = lato²

Area (Rettangolo) = lunghezza * larghezza

Esempio: Un prisma con una base rettangolare di 10 cm di lunghezza e 6 cm di larghezza avrà un'area di base di 10 cm * 6 cm = 60 cm².

Prisma a Base Pentagonale o Esagonale (e Altri Poligoni Regolari)

Calcolare l'area di base di un prisma con una base poligonale regolare (come un pentagono o un esagono) richiede un approccio leggermente diverso. Si utilizza la formula:

Area = (1/2) * perimetro * apotema

Dove:

"perimetro" è la somma delle lunghezze di tutti i lati del poligono.
"apotema" è la distanza dal centro del poligono al punto medio di un lato.

Esempio: Consideriamo un prisma con una base esagonale regolare. Supponiamo che ogni lato dell'esagono misuri 4 cm e l'apotema sia di circa 3.46 cm. Il perimetro sarebbe 6 * 4 cm = 24 cm. L'area della base sarebbe (1/2) * 24 cm * 3.46 cm = 41.52 cm² (circa).

Consiglio: A volte, anziché l'apotema, potrebbe essere fornito il raggio del poligono (la distanza dal centro a un vertice). In questo caso, è necessario utilizzare la trigonometria o altre relazioni geometriche per calcolare l'apotema.

Prisma a Base Circolare (Cilindro)

Un cilindro è un caso speciale di prisma dove le basi sono cerchi. L'area di un cerchio è data da:

Area = π * r²

Dove:

"π" (pi greco) è una costante approssimativamente uguale a 3.14159.
"r" è il raggio del cerchio (la distanza dal centro del cerchio a un punto qualsiasi sulla circonferenza).

Esempio: Se un cilindro ha un raggio di 5 cm, l'area di base sarà π * (5 cm)² = π * 25 cm² ≈ 78.54 cm².

Errori Comuni da Evitare

Quando si calcola l'area di base di un prisma, è facile commettere errori. Ecco alcuni dei più comuni:

Confondere l'altezza del prisma con l'altezza della base: Sono due misure completamente diverse! L'altezza del prisma è la distanza tra le due basi, mentre l'altezza della base (nel caso di triangoli o altri poligoni) è una dimensione della base stessa.
Usare unità di misura incoerenti: Assicurati che tutte le tue misure siano nella stessa unità (es. tutti in centimetri, metri, ecc.). Se hai misure in unità diverse, convertile prima di eseguire i calcoli.
Dimenticare di usare l'unità di misura corretta per l'area: L'area è sempre misurata in unità quadrate (es. cm², m², ecc.).
Non identificare correttamente la forma della base: Prima di applicare qualsiasi formula, assicurati di aver identificato correttamente la forma della base del prisma. Un errore qui renderà tutti i calcoli successivi sbagliati.

Consigli Pratici per il Successo

Ecco alcuni consigli per aiutarti a calcolare l'area di base di un prisma con successo:

Disegna sempre un diagramma: Un disegno ti aiuterà a visualizzare il problema e a identificare le misure necessarie.
Scrivi la formula: Scrivere la formula prima di inserire i numeri ti aiuterà a evitare errori.
Controlla il tuo lavoro: Dopo aver eseguito i calcoli, ricontrolla attentamente per assicurarti di non aver commesso errori.
Usa una calcolatrice: Una calcolatrice può aiutarti a eseguire i calcoli in modo rapido e preciso.
Esercitati, esercitati, esercitati: Più ti eserciti, più diventerai bravo a calcolare l'area di base di un prisma.

Calcolare l'area di base di un prisma può sembrare complicato all'inizio, ma con la giusta comprensione dei concetti e un po' di pratica, diventerà una competenza naturale. Ricorda, l'importante è identificare correttamente la forma della base e utilizzare la formula appropriata. Buona fortuna!