Area Di Base Di Un Cono

Hai mai ammirato la forma perfetta di un gelato nel cono, o la maestosità di una montagna che si erge verso il cielo? Entrambi, a modo loro, ci ricordano una figura geometrica fondamentale: il cono. Ma cosa rende un cono tale e quale, e come possiamo capire la sua base? Questo articolo è pensato per te, studente delle scuole medie o superiori, appassionato di matematica o semplicemente curioso di scoprire i segreti delle forme che ci circondano. Esploreremo insieme l'area di base di un cono, fornendo una guida chiara e comprensibile.

Cos'è un Cono?

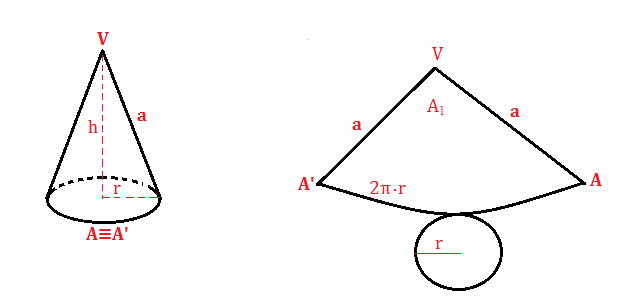
Prima di addentrarci nel calcolo dell'area di base, è importante definire con precisione cosa intendiamo per cono. Immagina un cerchio, perfetto e piatto. Ora, prendi un punto al di fuori di questo cerchio, nello spazio. Se connetti ogni punto della circonferenza del cerchio a quel punto esterno, ottieni un cono.

Un cono è quindi un solido geometrico delimitato da:

• Un cerchio, chiamato base.
• Un punto esterno al cerchio, chiamato vertice.
• Una superficie laterale, che connette la circonferenza della base al vertice.

La distanza dal vertice al centro della base è detta altezza del cono. La distanza dal vertice a un qualsiasi punto della circonferenza della base è detta apotema.

L'Importanza della Base

La base del cono è un elemento cruciale per diverse ragioni: determina la sua forma, influisce sul suo volume e sulla sua superficie totale, ed è fondamentale per calcolare molte delle sue proprietà geometriche. Capire come calcolare l'area di base è quindi un passo fondamentale per comprendere il cono nella sua interezza.

Area di Base: Un Cerchio Perfetto

La base di un cono, come abbiamo detto, è un cerchio. Quindi, per calcolare l'area di base, dobbiamo semplicemente calcolare l'area di un cerchio.

Ma come si calcola l'area di un cerchio? La formula è relativamente semplice e si basa su un numero magico: π (pi greco), che approssimativamente vale 3.14159.

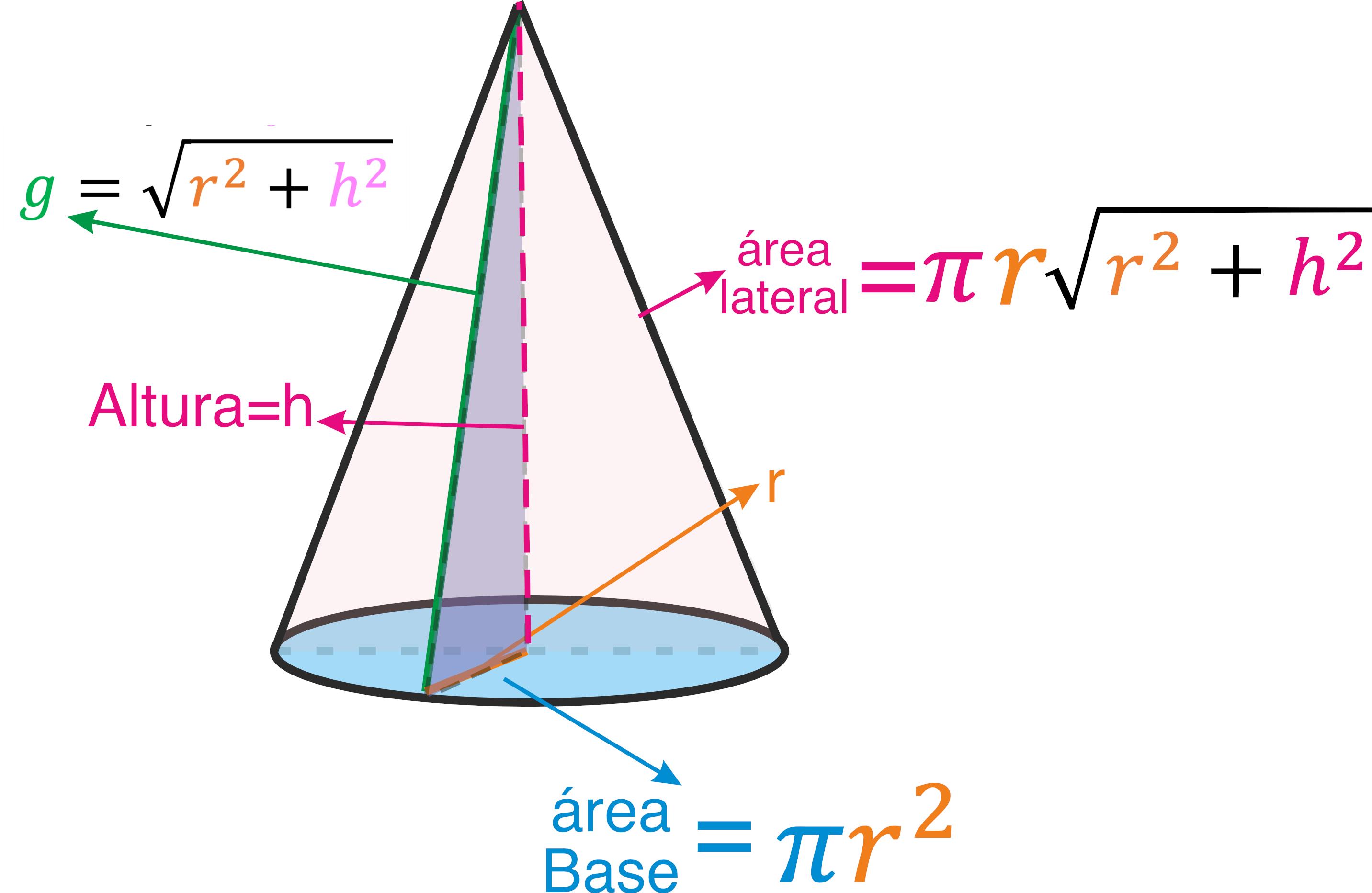
La formula per l'area di un cerchio è:

Area = π * r²

Dove:

• Area è l'area del cerchio (e quindi l'area di base del cono).
• π (pi greco) è una costante matematica approssimativamente uguale a 3.14159.
• r è il raggio del cerchio (la distanza dal centro del cerchio a qualsiasi punto sulla sua circonferenza).

Esempi Pratici

Vediamo ora alcuni esempi pratici per capire meglio come applicare questa formula:

Esempio 1: Cono con raggio noto

Supponiamo di avere un cono con un raggio di base di 5 cm. Vogliamo calcolare l'area di base.

1. Identifichiamo il raggio: r = 5 cm.
2. Applichiamo la formula: Area = π * r² = π * 5² = π * 25 ≈ 3.14159 * 25 ≈ 78.54 cm².

Quindi, l'area di base del cono è approssimativamente 78.54 cm².

Esempio 2: Cono con diametro noto

Invece del raggio, potremmo conoscere il diametro della base del cono. Ricorda che il diametro è il doppio del raggio (d = 2r).

Supponiamo di avere un cono con un diametro di base di 10 cm. Vogliamo calcolare l'area di base.

1. Calcoliamo il raggio: r = d / 2 = 10 cm / 2 = 5 cm.
2. Applichiamo la formula: Area = π * r² = π * 5² = π * 25 ≈ 3.14159 * 25 ≈ 78.54 cm².

Ancora una volta, l'area di base del cono è approssimativamente 78.54 cm².

Esempio 3: Applicazione nel mondo reale

Immagina di voler costruire un cappello a forma di cono per una festa. Vuoi che la base del cappello abbia un diametro di 20 cm. Quanta carta ti servirà per tagliare la base?

1. Calcoliamo il raggio: r = d / 2 = 20 cm / 2 = 10 cm.
2. Applichiamo la formula: Area = π * r² = π * 10² = π * 100 ≈ 3.14159 * 100 ≈ 314.16 cm².

Avrai bisogno di circa 314.16 cm² di carta per tagliare la base del tuo cappello.

Consigli Utili

• Assicurati di utilizzare le stesse unità di misura per tutte le grandezze (ad esempio, se il raggio è in centimetri, l'area sarà in centimetri quadrati).
• Quando utilizzi π, puoi usare un'approssimazione (come 3.14) o la funzione π della tua calcolatrice per ottenere un risultato più preciso.
• Se hai difficoltà a ricordare la formula, pensa al cerchio come una pizza: per sapere quanta pizza hai, devi conoscere il suo raggio!

Perché è Importante?

Capire come calcolare l'area di base di un cono non è solo un esercizio di matematica. È una competenza che può essere utile in molte situazioni pratiche: dalla costruzione di oggetti di artigianato al calcolo della quantità di materiale necessario per un progetto di design. La matematica ci aiuta a comprendere e a interagire con il mondo che ci circonda.

Oltre l'Area di Base

Ora che hai imparato a calcolare l'area di base di un cono, sei pronto per esplorare altre proprietà di questa affascinante figura geometrica. Potresti voler approfondire il calcolo del volume del cono, della sua superficie laterale, o studiare le relazioni tra il cono e altre figure geometriche come il cilindro e la sfera.

Ricorda che la matematica è un viaggio, non una destinazione. Continua a esplorare, a sperimentare e a porre domande. Più impari, più sarai in grado di apprezzare la bellezza e la potenza dei concetti matematici che ci circondano.

Conclusione

Speriamo che questo articolo ti abbia fornito una comprensione chiara e completa dell'area di base di un cono. Ricorda la formula (Area = π * r²), esercitati con gli esempi e non aver paura di esplorare ulteriormente. Con un po' di pratica, sarai in grado di calcolare l'area di base di qualsiasi cono con facilità e sicurezza. E chissà, magari la prossima volta che mangerai un gelato nel cono, penserai con un sorriso a π e al suo magico potere!