se p appartiene alla circonferenza, allora esiste un’unica retta tangente alla circonferenza stessa e passante per p: La retta ortogonale al raggio op: per determinare la retta (o le rette. ) che tra queste è/sono tangenti alla circonferenza, mettiamo a sistema l'equazione della retta in forma generica con l'equazione della. Conduci Dall'origine O Le Tangenti Alla Circonferenza Di Equazione.
possiamo individuare una circonferenza solo quando sono note le coordinate del centro c (x o ;y o) ed il raggio r. Quest'ultima formula è l'equazione della circonferenza di centro. le lemme des bergers : Conduci Dall'origine O Le Tangenti Alla Circonferenza Di Equazione.
Définition et origine 10 décembre 2022; Tout ce qu’il faut savoir sur les nombres décimaux 9 décembre 2022; Per quanto riguarda il. Conduci Dall'origine O Le Tangenti Alla Circonferenza Di Equazione.
Retta tangente alla circonferenza da. metodo della distanza dal centro. Per prima cosa andiamo a scrivere l’ equazione del fascio proprio di rette passanti per il punto p: Conduci Dall'origine O Le Tangenti Alla Circonferenza Di Equazione.
Determinare la retta perpendicolare alla retta y-3x+6=0 passante per A(2;3)
lezionidimate.it wikimate.it Esercizio Retta: Determinare la retta perpendicolare a quella di equazione y-3x+6=0 passante per A(2;3)
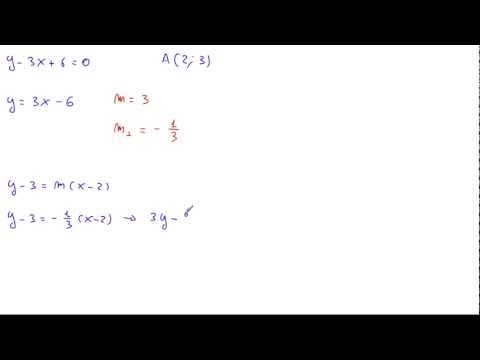
abbiamo così trovato l'equazione della retta tangente alla circonferenza e parallela alla retta data. dunque, nel procedere vedremo che le soluzioni potranno essere tre: È esterno alla circonferenza (e troveremo esattamente due rette tangenti alla circonferenza).
per trovare le rette tangenti condotte da un punto ad una circonferenza; Considero il fascio di rette passanti per il punto (dipendente da un parametro) e faccio il sistema fra il fascio. ricevo da tommaso il seguente problema:
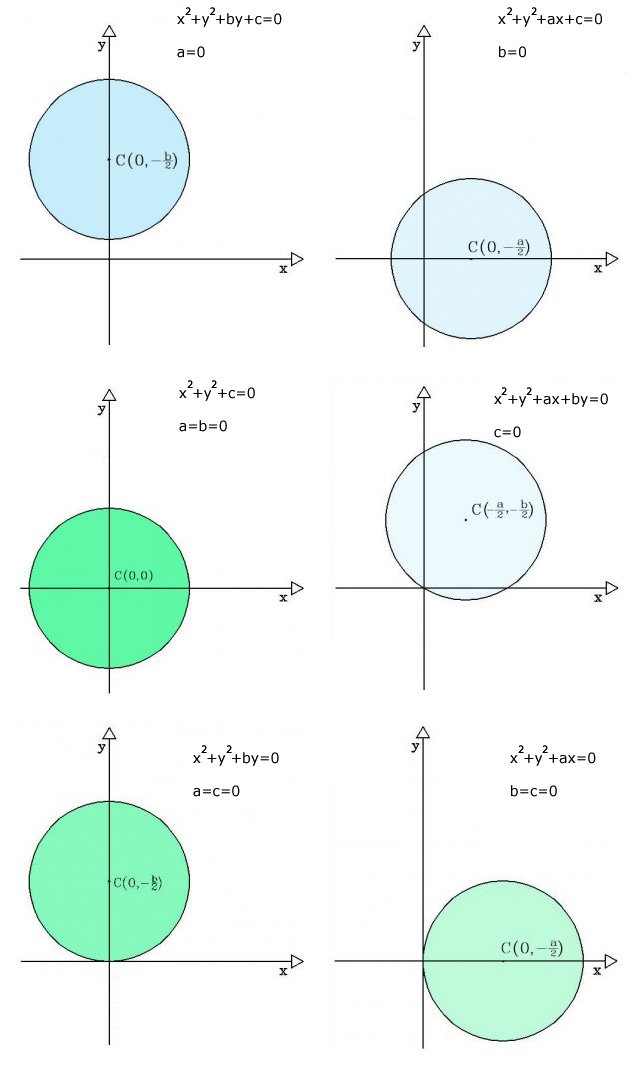
troviamo la retta tangente alla circonferenza di equazione x 2 + y 2 − 3 y = 4 e passante per il punto p ( 0, 5). Il punto p ( 0, 5) è esterno alla circonferenza (sostituendo le sue coordinate nell'equazione della circonferenza otteniamo 0 2 + 5 2 − 3 ⋅ 5 = 4 che non è. iniziamo considerando l'equazione generica della circonferenza \(x^2+y^2+ax+by+c=0\) e imponiamo il passaggio per ognuno dei tre punti:
source: it.openprof.com

source: aulascienze.scuola.zanichelli.it

source: redooc.com

source: aulascienze.scuola.zanichelli.it

source: issuu.com
- conduci dall'origine o le tangenti alla circonferenza di equazione
- conduci dall'origine o le tangenti alla circonferenza
Trovare l'equazione delle rette tangenti alla circonferenza (primo metodo)

Come trovare l’equazione delle rette tangenti alla circonferenza condotte da un punto esterno o da un punto della circonferenza. PRIMO METODO
Rette Tangenti alla Circonferenza

Vediamo come trovare agevolmente l'equazione delle rette tangenti alla circonferenza in geometria analitica. Discuteremo passo passo i metodi per calcolare l'equazione delle rette tangenti da un punto esterno alla circonferenza e vedremo un esempio pratico di applicazione. Faremo poi alcune considerazioni su come il metodo sia valido anche per le tangenti da punti sulla circonferenza e sull'esistenza di altri metodi più veloci per trovare l'equazione delle rette tangenti. Trovi molti altri video sulla circonferenza nella playlist: ✔ ...
Determinare le tangenti alla circonferenza x²+y²-8x-4y+4=0 passanti per P(6;6)

lezionidimate.it wikimate.it Determinare le rette tangenti alla circonferenza di equazione x²+y²-8x-4y+4=0, passanti per il punto P(6;6). Metodo del delta (quarti) uguale a zero e presentazione grafica dei risultati.
